Top 12 Functional Equations And How To Solve Them Pdf 455 People Liked This Answer

You are looking for information, articles, knowledge about the topic nail salons open on sunday near me functional equations and how to solve them pdf on Google, you do not find the information you need! Here are the best content compiled and compiled by the Chewathai27.com team, along with other related topics such as: functional equations and how to solve them pdf Topics in functional equations PDF, Functional equation pdf, 100 functional equations Problems pdf, Awesome polynomials for mathematics competitions PDF, Function Equation Titu, 117 polynomial problems pdf, Functional equation problems, Polynomial Olympiad pdf

Contents

What are the 4 types of functions in math?

The types of functions can be broadly classified into four types. Based on Element: One to one Function, many to one function, onto function, one to one and onto function, into function.

What is an example of functional?

The definition of functional is something that is useful for its intended purpose. A saw that works to cut things is an example of a functional saw. Of or relating to a function.

What are the 12 types of functions?

Terms in this set (12)

Quadratic. f(x)=x^2. D: -∞,∞ R: 0,∞
Reciprocal. f(x)=1/x. D: -∞,0 U 0,∞ R: -∞,0 U 0,∞ Odd.
Exponential. f(x)=e^x. D: -∞,∞ R: 0,∞
Sine. f(x)=SINx. D: -∞,∞ R: -1,1. Odd.
Greatest Integer. f(x)= [[x]] D: -∞,∞ R: {All Integers} Neither.
Absolute Value. f(x)= I x I. D: -∞,∞ R: 0,∞ …
Linear. f(x)=x. Odd.
Cubic. f(x)=x^3. Odd.

What are the 8 types of functions?

The eight types are linear, power, quadratic, polynomial, rational, exponential, logarithmic, and sinusoidal.

What is function explain the types of function with examples?

A Rational function is a sort of function which is derived from the ratio of two given polynomial functions and is expressed as, f ( x ) = P ( x ) Q ( x ) , such that P and Q are polynomial functions of x and Q(x) ≠ 0. For example, f ( x ) = ( x 2 + 4 x + 5 ) x 2 − 4 is a rational function.

What is the meaning of functional equation?

In mathematics, a functional equation is, in the broadest meaning, an equation in which one or several functions appear as unknowns. So, differential equations and integral equations are functional equations.

What is a functional in math?

A functional is a real-valued function on a vector space , usually of functions. For example, the energy functional on the unit disk assigns a number to any differentiable function , For the functional to be continuous, it is necessary for the vector space. of functions to have an appropriate topology.

What is not a function equation?

Vertical lines are not functions. The equations y = ± x and x 2 + y 2 = 9 are examples of non-functions because there is at least one -value with two or more -values.

What is function explain with example?

An example of a simple function is f(x) = x². In this function, the function f(x) takes the value of “x” and then squares it. For instance, if x = 3, then f(3) = 9. A few more examples of functions are: f(x) = sin x, f(x) = x² + 3, f(x) = 1/x, f(x) = 2x + 3, etc.

A Beautiful trick for Functional Equations| Putnam 1988 A5

functional equations and how to solve them pdf

Article author: www.isinj.com
Reviews from users: 27251 Ratings
Top rated: 4.4
Lowest rated: 1
Summary of article content: Articles about functional equations and how to solve them pdf Our em- phasis is on the development of those tools which are most useful in giving a family of solutions to each functional equation in explicit form. At the … …
Most searched keywords: Whether you are looking for functional equations and how to solve them pdf Our em- phasis is on the development of those tools which are most useful in giving a family of solutions to each functional equation in explicit form. At the …
Table of Contents:

functional equations and how to solve them pdf

Article author: www.pdfdrive.com
Reviews from users: 16349 Ratings
Top rated: 4.5
Lowest rated: 1
Summary of article content: Articles about Functional Equations and How to Solve Them (Problem Books in Mathematics) by Christopher G. Small – PDF Drive Functional Equations and How to Solve Them (Problem Books in Mathematics) ; Solving problems in geometry: Insights and strategies for mathematical olympiad. 370 … …
Most searched keywords: Whether you are looking for Functional Equations and How to Solve Them (Problem Books in Mathematics) by Christopher G. Small – PDF Drive Functional Equations and How to Solve Them (Problem Books in Mathematics) ; Solving problems in geometry: Insights and strategies for mathematical olympiad. 370 …
Table of Contents:

Solving problems in geometry Insights and strategies for mathematical olympiad

Advanced book on Mathematics Olympiad

Problem Solving strategies for Math Olympiads

An Introduction to the Theory of Functional Equations and Inequalities Cauchy’s Equation and Jensen’s Inequality

Adventures in Problem Solving Mathematical Marvels by Shailesh Shirali Universities Press RMO INMO IMO Mathematics Olympiads

A First Step to Mathematical Olympiad Problems

How to Solve It A New Aspect of Mathematical Method

Problem Books in Mathematics

103 Trigonometry Problems From the Training of the USA IMO Team

equations inequalities and problem solving

Functional Equations and How to Solve Them (Problem Books in Mathematics) by Christopher G. Small - PDF Drive — Functional Equations and How to Solve Them (Problem Books in Mathematics) by Christopher G. Small – PDF Drive

Article author: link.springer.com
Reviews from users: 3748 Ratings
Top rated: 3.8
Lowest rated: 1
Summary of article content: Articles about Functional Equations and How to Solve Them | SpringerLink This book covers topics in the theory and practice of functional equations. Special emphasis is given to methods for solving functional equations that … …
Most searched keywords: Whether you are looking for Functional Equations and How to Solve Them | SpringerLink This book covers topics in the theory and practice of functional equations. Special emphasis is given to methods for solving functional equations that …
Table of Contents:

Editors

Sections

Buying options

Table of contents (8 chapters)

About this book

Keywords

Reviews

Editors and Affiliations

About the editor

Bibliographic Information

Buying options

Functional Equations and How to Solve Them | SpringerLink

Article author: www.msri.org
Reviews from users: 11041 Ratings
Top rated: 4.5
Lowest rated: 1
Summary of article content: Articles about functional equations and how to solve them pdf tional equations, as will become obvious once the reader solves the problems throughout this book. At the current time, thorough knowledge … …
Most searched keywords: Whether you are looking for functional equations and how to solve them pdf tional equations, as will become obvious once the reader solves the problems throughout this book. At the current time, thorough knowledge …
Table of Contents:

functional equations and how to solve them pdf

Article author: www.youtube.com
Reviews from users: 47700 Ratings
Top rated: 3.3
Lowest rated: 1
Summary of article content: Articles about Solving Functions: Tables, Graphs, Equations (Simplifying Math) – YouTube Updating …
Most searched keywords: Whether you are looking for Solving Functions: Tables, Graphs, Equations (Simplifying Math) – YouTube Updating Short lesson about solving Functions. This lesson shows how to determine the output for functions in tables, graphs and solving function equations.pre-algebra, lesson, function, functions, solve, input, output, domain, range, table, graph, equation, math, tutor, teacher, school, learn, student, Education, Lessons, Students, simplifying math, eric buffington, literature subject, short lesson, function equations, funktion, mathematics, graphs, field of study, tables graphs equations, tables, graph equation, calculus
Table of Contents:

Solving Functions: Tables, Graphs, Equations (Simplifying Math) - YouTube — Solving Functions: Tables, Graphs, Equations (Simplifying Math) – YouTube

Article author: www.youtube.com
Reviews from users: 5918 Ratings
Top rated: 4.7
Lowest rated: 1
Summary of article content: Articles about Solving a Functional Equation – YouTube Updating …
Most searched keywords: Whether you are looking for Solving a Functional Equation – YouTube Updating This video is about a Functional EquationMy merch: https://teespring.com/stores/sybermath?page=1Follow me: https://twitter.com/SyberMath Subscribe!!!: https:…algebra, algebraic equations, SyberMath, algebraic manipulations, equations, substitution, Challenging Math Problems, Non-routine Math Problems, algebraic identities, non-standard methods, symmetry, math, maths, mathematics, an algebraic challenge
Table of Contents:

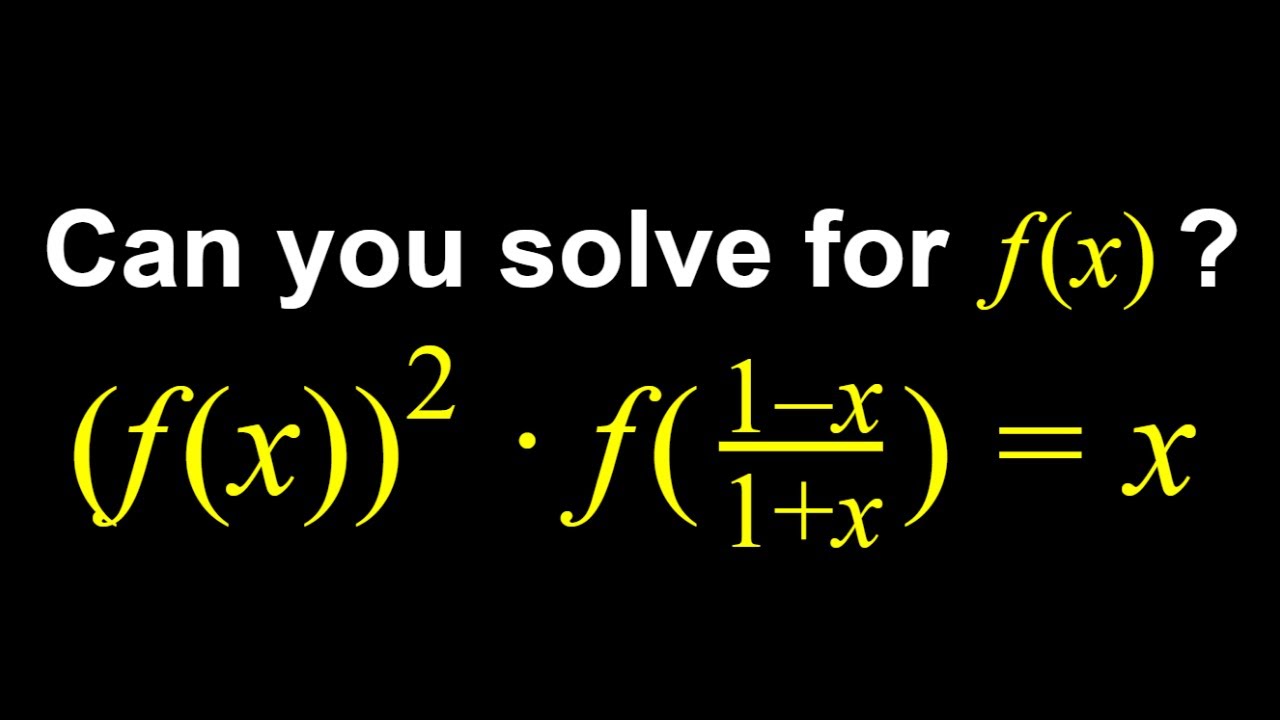
Solving a Functional Equation - YouTube — Solving a Functional Equation – YouTube

Article author: www.youtube.com
Reviews from users: 5834 Ratings
Top rated: 3.8
Lowest rated: 1
Summary of article content: Articles about Problem Solving with Function Notation – YouTube Updating …
Most searched keywords: Whether you are looking for Problem Solving with Function Notation – YouTube Updating Understand how to develop equations in function notation form to solve a problemFunctional Notation, Problem Solving (Literature Subject), Anil kumar, anil kumar math, aan learning centre, iit, jee, iit jee, anil kumar iit, anil kumar sat, sat, tips, mcr, grade 11, grade 12, algebra 2, mcr3u, mch4u, mcr4u, pre-calculus, functions, relations, domain, range, vertical line test, anil kumar functions, function notation, independent variable, dependent, variable, f(x)
Table of Contents:

Problem Solving with Function Notation - YouTube — Problem Solving with Function Notation – YouTube

Article author: www.cuemath.com
Reviews from users: 9534 Ratings
Top rated: 3.4
Lowest rated: 1
Summary of article content: Articles about Types of Functions – Types, Definition, Examples Updating …
Most searched keywords: Whether you are looking for Types of Functions – Types, Definition, Examples Updating The types of functions are defined on the basis of domain, range, and function expression. The expression used to write the function is the prime defining factor for a function.
Table of Contents:

What are the Different Types of Functions

Representation of Functions

List of Types of Functions

Types of Functions – Based on Set Elements

Types of Function – Based on Equation

Types of Functions – Based on Range

Types oF Functions – Based on Domain

Solved Examples on Types of Functions

Practice Questions on Types of Functions

FAQs on Types of Functions

Types of Functions – Types, Definition, Examples

Article author: docero.com.br
Reviews from users: 41179 Ratings
Top rated: 4.7
Lowest rated: 1
Summary of article content: Articles about Functional Equations & How to Solve Them – Baixar pdf de Doceru.com Functional Equations & How to Solve Them – documento [*.pdf] Problem Books in Mathematics Edited by P. Winkler Problem Books in Mathematics … …
Most searched keywords: Whether you are looking for Functional Equations & How to Solve Them – Baixar pdf de Doceru.com Functional Equations & How to Solve Them – documento [*.pdf] Problem Books in Mathematics Edited by P. Winkler Problem Books in Mathematics … Functional Equations & How to Solve Them – documento [*.pdf] Problem Books in Mathematics Edited by P. Winkler Problem Books in Mathematics Series Editor: Peter Winkler Pell’s Equation by Edward J. Barbeau Polynomials by Edward J. Barbeau Problems…Functional, Equations, &, How, to, Solve, Them, -, Baixar, pdf, de, Doceru.com
Table of Contents:

Functional Equations & How to Solve Them - Baixar pdf de Doceru.com — Functional Equations & How to Solve Them – Baixar pdf de Doceru.com

Article author: cdn.bc-pf.org
Reviews from users: 34345 Ratings
Top rated: 4.7
Lowest rated: 1
Summary of article content: Articles about functional equations and how to solve them pdf General solution: a family of solutions to a functional equation which respects these two conditions: – Any function in the given form indeed is … …
Most searched keywords: Whether you are looking for functional equations and how to solve them pdf General solution: a family of solutions to a functional equation which respects these two conditions: – Any function in the given form indeed is …
Table of Contents:

functional equations and how to solve them pdf

Article author: www.semanticscholar.org
Reviews from users: 8196 Ratings
Top rated: 3.1
Lowest rated: 1
Summary of article content: Articles about [PDF] Functional Equations and How to Solve Them | Semantic Scholar A of functional equations is investigated, giving representations or existence theorems for the solutions, and the main tools in the … …
Most searched keywords: Whether you are looking for [PDF] Functional Equations and How to Solve Them | Semantic Scholar A of functional equations is investigated, giving representations or existence theorems for the solutions, and the main tools in the … An historical introduction.- Functional equations with two variables.- Functional equations with one variable.- Miscellaneous methods for functional equations.- Some closing heuristics.- Appendix: Hamel bases.- Hints and partial solutions to problems.
Table of Contents:

58 Citations

References

Functional Equations and How to Solve Them

This book covers topics in the theory and practice of functional equations. Special emphasis is given to methods for solving functional equations that appear in mathematics contests, such as the Putnam competition and the International Mathematical Olympiad. This book will be of particular interest to university students studying for the Putnam competition, and to high school students working to improve their skills on mathematics competitions at the national and international level. Mathematics educators who train students for these competitions will find a wealth of material for training on functional equations problems.

The book also provides a number of brief biographical sketches of some of the mathematicians who pioneered the theory of functional equations. The work of Oresme, Cauchy, Babbage, and others, is explained within the context of the mathematical problems of interest at the time.

Christopher Small is a Professor in the Department of Statistics and Actuarial Science at the University of Waterloo. He has served as the co-coach on the Canadian team at the IMO (1997, 1998, 2000, 2001, and 2004), as well as the Waterloo Putnam team for the William Lowell Putnam Competition (1986-2004). His previous books include Numerical Methods for Nonlinear Estimating Equations (Oxford 2003), The Statistical Theory of Shape (Springer 1996), Hilbert Space Methods in Probability and Statistical Inference (Wiley 1994).

From the reviews:

Functional Equations and How to Solve Them fills a need and is a valuable contribution to the literature of problem solving.

– Henry Ricardo, MAA Reviews

The main purpose and merits of the book…are the many solved, unsolved, partially solved problems and hints about several particular functional equations.

– Janos Aczel, Zentralblatt

Functional Equations & How to Solve Them

Problem Books in Mathematics

Edited by P. Winkler

Problem Books in Mathematics

Series Editor: Peter Winkler

Pell’s Equation

by Edward J. Barbeau

Polynomials

by Edward J. Barbeau

Problems in Geometry

by Marcel Berger, Pierre Pansu, Jean-Pic Berry, and Xavier Saint-Raymond

Problem Book for First Year Calculus

by George W. Bluman

Exercises in Probability

by T. Cacoullos

Probability Through Problems

by Marek Capiński and Tomasz Zastawniak

An Introduction to Hilbert Space and Quantum Logic

by David W. Cohen

Unsolved Problems in Geometry

by Hallard T. Croft, Kenneth J. Falconer, and Richard K. Guy

Berkeley Problems in Mathematics, (Third Edition)

by Paulo Ney de Souza and Jorge-Nuno Silva

The IMO Compendium: A Collection of Problems Suggested for the

International Mathematical Olympiads: 1959-2004

by Dušan Djukić, Vladimir Z. Janković, Ivan Matić, and Nikola Petrović

Problem-Solving Strategies

by Arthur Engel

Problems in Analysis

by Bernard R. Gelbaum

Problems in Real and Complex Analysis

by Bernard R. Gelbaum

(continued after index)

Christopher G. Small

Functional Equations

and How to Solve Them

Mathematics Subject Classification (2000): 39-xx

Library of Congress Control Number: 2006929872

ISBN-10: 0-387-34534-5 e-ISBN-10: 0-387-48901-0

ISBN-13: 978-0-387-34534-5 e-ISBN-13: 978-0-387-48901-8

Printed on acid-free paper.

© 2007 Springer Science+Business Media, LLC

All rights reserved. This work may not be translated or copied in whole or in part without the

written permission of the publisher (Springer Science+Business Media, LLC, 233 Spring Street,

New York, NY 10013, USA), except for with reviews or scholarly analysis. Use in connection

with any form of information storage and retrie computer software, or by similar or dissimilar

methodology now known or hereafter developed is forbidden.

The use in this publication of trade names, trademarks, service marks, and similar terms, even if

they are not identified as such, is not to be taken as an expression of opinion as to whether or

not they are subject to proprietary rights.

9 8 7 6 5 4 3 2 1

springer.com

Christopher G. Small

Department of Statistics & Actuarial Science

University of Waterloo

200 University Avenue West

Waterloo N2L 3G1

Canada

[email protected]

Series Editor:

Peter Winkler

Department of Mathematics

Dartmouth College

Hanover, NH 03755

USA

[email protected]

2

x

1

-1

f(x)

-1

-1.5

0

-2

1.5

0

1

0.5

2

-0.5

f(x) + f(2 x) + f(3 x) = 0

for all real x.

This functional equation is satisﬁed by the function f(x) ≡ 0, and also by

the strange example graphed above. To ﬁnd out more about this function, see

Chapter 3.

2

x

0

-2

4

-4

2

0

-2

-4

f(x)

4

f(f(f(x))) = x

Can you discover a function f(x) which satisﬁes this functional equation?

Contents

Preface . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ix

1 An historical introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1

1.1 Preliminary remarks . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1

1.2 Nicole Oresme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1

1.3 Gregory of Saint-Vincent . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

1.4 Augustin-Louis Cauchy. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6

1.5 What about calculus? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8

1.6 Jean d’Alembert . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9

1.7 Charles Babbage . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10

1.8 Mathematics competitions and recreational mathematics . . . . . 16

1.9 A contribution from Ramanujan . . . . . . . . . . . . . . . . . . . . . . . . . . . 21

1.10 Simultaneous functional equations . . . . . . . . . . . . . . . . . . . . . . . . . 24

1.11 A clariﬁcation of terminology . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25

1.12 Existence and uniqueness of solutions . . . . . . . . . . . . . . . . . . . . . . 26

1.13 Problems . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26

2 Functional equations with two variables. . . . . . . . . . . . . . . . . . . . 31

2.1 Cauchy’s equation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31

2.2 Applications of Cauchy’s equation . . . . . . . . . . . . . . . . . . . . . . . . . 35

2.3 Jensen’s equation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37

2.4 Linear functional equation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38

2.5 Cauchy’s exponential equation . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38

2.6 Pexider’s equation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39

2.7 Vincze’s equation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40

2.8 Cauchy’s inequality . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42

2.9 Equations involving functions of two variables . . . . . . . . . . . . . . . 43

2.10 Euler’s equation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44

2.11 D’Alembert’s equation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45

2.12 Problems . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 49

viii Contents

3 Functional equations with one variable. . . . . . . . . . . . . . . . . . . . . 55

3.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55

3.2 Linearization. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55

3.3 Some basic families of equations . . . . . . . . . . . . . . . . . . . . . . . . . . . 57

3.4 A menagerie of conjugacy equations . . . . . . . . . . . . . . . . . . . . . . . 62

3.5 Finding solutions for conjugacy equations. . . . . . . . . . . . . . . . . . . 64

3.5.1 The Koenigs algorithm for Schröder’s equation . . . . . . . . 64

3.5.2 The Lévy algorithm for Abel’s equation . . . . . . . . . . . . . . 66

3.5.3 An algorithm for Böttcher’s equation . . . . . . . . . . . . . . . . 66

3.5.4 Solving commutativity equations . . . . . . . . . . . . . . . . . . . . 67

3.6 Generalizations of Abel’s and Schröder’s equations . . . . . . . . . . . 67

3.7 General properties of iterative roots. . . . . . . . . . . . . . . . . . . . . . . . 69

3.8 Functional equations and nested radicals . . . . . . . . . . . . . . . . . . . 72

3.9 Problems . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 75

4 Miscellaneous methods for functional equations . . . . . . . . . . . . 79

4.1 Polynomial equations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79

4.2 Power series methods . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 81

4.3 Equations involving arithmetic functions . . . . . . . . . . . . . . . . . . . 82

4.4 An equation using special groups . . . . . . . . . . . . . . . . . . . . . . . . . . 87

4.5 Problems . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89

5 Some closing heuristics . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 91

6 Appendix: Hamel bases . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 93

7 Hints and partial solutions to problems . . . . . . . . . . . . . . . . . . . . 97

7.1 A warning to the reader . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 97

7.2 Hints for Chapter 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 97

7.3 Hints for Chapter 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 102

7.4 Hints for Chapter 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 107

7.5 Hints for Chapter 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 113

8 Bibliography . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 123

Index . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 125

Preface

Over the years, a number of books have been written on the theory of func-

tional equations. However, few books have been published on solving func-

tional equations which arise in mathematics competitions and mathematical

problem solving. The intention of this book is to go some distance towards

ﬁlling this gap.

This work began life some years ago as a set of training notes for

mathematics competitions such as the William Lowell Putnam Competition

for undergraduate university students, and the International Mathematical

Olympiad for high school students. As part of the training for these competi-

tions, I tried to put together some systematic material on functional equations,

which have formed a part of the International Mathematical Olympiad and a

small component of the Putnam Competition. As I became more involved

in coaching students for the Putnam and the International Mathematical

Olympiad, I started to understand why there is not much training mate-

rial available in systematic form. Many would argue that there is no theory

attached to functional equations that are encountered in mathematics compe-

titions. Each such equation requires diﬀerent techniques to solve it. Functional

equations are often the most diﬃcult problems to be found on mathematics

competitions because they require a minimal amount of background theory

and a maximal amount of ingenuity. The great advantage of a problem involv-

ing functional equations is that you can construct problems that students at

all levels can understand and play with. The great disadvantage is that, for

many problems, few students can make much progress in ﬁnding solutions even

if the required techniques are essentially elementary in nature. It is perhaps

this view of functional equations which explains why most problem-solving

texts have little systematic material on the subject. Problem books in mathe-

matics usually include some functional equations in their chapters on algebra.

But by including functional equations among the problems on polynomials or

inequalities the essential character of the methodology is often lost.

As my training notes grew, so grew my conviction that we often do not do

full justice to the role of theory in the solution of functional equations. The

x Preface

result of my growing awareness of the interplay between theory and problem

application is the book you have before you. It is based upon my belief that

a ﬁrm understanding of the theory is useful in practical problem solving with

such equations. At times in this book, the marriage of theory and practice is

not seamless as there are theoretical ideas whose practical utility is limited.

However, they are an essential part of the subject that could not be omit-

ted. Moreover, today’s theoretical idea may be the inspiration for tomorrow’s

competition problem as the best problems often arise from pure research. We

shall have to wait and see.

The student who encounters a functional equation on a mathematics con-

test will need to investigate solutions to the equation by ﬁnding all solutions

(if any) or by showing that all solutions have a particular property. Our em-

phasis is on the development of those tools which are most useful in giving a

family of solutions to each functional equation in explicit form.

At the end of each chapter, readers will ﬁnd a list of problems associated

with the material in that chapter. The problems vary greatly in diﬃculty,

with the easiest problems being accessible to any high school student who has

read the chapter carefully. It is my hope that the most diﬃcult problems are

a reasonable challenge to advanced students studying for the International

Mathematical Olympiad at the high school level or the William Lowell Put-

nam Competition for university undergraduates. I have placed stars next to

those problems which I consider to be the harder ones. However, I recognise

that determining the level of diﬃculty of a problem is somewhat subjective.

What one person ﬁnds diﬃcult, another may ﬁnd easy.

In writing these training notes, I have had to make a choice as to the gen-

erality of the topics covered. The modern theory of functional equations can

occur in a very abstract setting that is quite inappropriate for the readership

I have in mind. However, the abstraction of some parts of the modern theory

reﬂects the fact that functional equations can occur in diverse settings: func-

tions on the natural numbers, the integers, the reals, or the complex numbers

can all be studied within the subject area of functional equations. Most of the

time, the functions I have in mind are real-valued functions of a single real

variable. However, I have tried not to be too restrictive in this. The reader will

also ﬁnd functions with complex arguments and functions deﬁned on natural

numbers in these pages. In some cases, equations for functions between circles

will also crop up. Nor are functional inequalities ignored.

One word of warning is in order. You cannot study functional equations

without making some use of the properties of limits and continuous functions.

The fact is that many problems involving functional equations depend upon

an assumption of such as continuity or some other regularity assumption that

would usually not be encountered until university. This presents a diﬃculty

for high school mathematics contests where the properties of limits and conti-

nuity cannot be assumed. One way to get around this problem is to substitute

another regularity condition that is more acceptable for high school mathe-

matics. Thus a problem where a continuity condition is natural may well get

Preface xi

by with the assumption of monotonicity. Although continuity and monotonic-

ity are logically independent properties (in the sense that neither implies the

other) the imposition of a monotonicity condition in a functional equations

problem may serve the same purpose as continuity. Another way around the

problem is to ask students to provide a weaker conclusion that is not “ﬁnished”

by invoking continuity. Asking students to determine the nature of a function

on the rational numbers is an example of this. Neither solution to this problem

is completely satisfactory. Fortunately, there are enough problems which can

be posed and solved using high school mathematics to serve the purpose. More

advanced contests such as the William Lowell Putnam Competition have no

such restrictions in imposing continuity or convexity, and expect the student

to treat these assumptions with mathematical maturity.

Some readers may be surprised to ﬁnd that the chapter on functional

equations in a single variable follows that on functional equations in two or

more variables. However this is the correct order. An equation in two or more

variables is formally equivalent to a family of simultaneous equations in one

variable. So equations in two variables give you more to play with. I have

had to be very selective in choosing topics in the third chapter, because much

of the academic literature is devoted to establishing uniqueness theorems for

solutions within particular families of functions: functions that are convex or

real analytic, functions which obey certain order conditions, and so on. It

would be easy to simply ignore the entire subject if it were not for the fact

that functional equations in a single variable are commonplace in mathematics

competitions. So I have done my best to present those tools and unifying

concepts which occur periodically in such problems in both high school and

university competitions. Chapter 3 has been written with a conﬁdence that

advanced high school students will adapt well to the challenge of a bit of

introductory university level mathematics. The chapters can be read more-or-

less independently of each other. There are some results in later chapters which

depend upon earlier chapters. However, the reader who wishes to sample the

book in random order can probably piece together the necessary information.

The fact that it is possible to write a book whose chapters are not heavily

dependent is a consequence of the character of functional equations. Unlike

some branches of mathematics, the subject is wide, providing easier access

from a number of perspectives. This makes it an excellent area for competition

problems. Even tough functional equations are relatively easy to state and

provide lots of “play value” for students who may not be able to solve them

completely.

Because this is a book about problem solving, the reader may be surprised

to ﬁnd that it begins with a chapter of the history of the subject. It is my

belief that the present way of teaching mathematics to students puts much

emphasis on the tools of mathematics, and not enough on the intellectual

climate which gave rise to these ideas. Functional equations were posed and

solved for reasons that had much to do with the intellectual challenges of

xii Preface

their times. This book attempts to provide a small glimpse of some of those

reasons.

I have learned much about functional equations from other people. This

book also owes much to others. So this preface would not be complete with-

out some mention of the debts that I owe. I have learned much from the

work of Janos Aczél, Distinguished Professor Emeritus at the University of

Waterloo. The impact of his work and that of his colleagues is to be found

throughout the following pages in places too numerous to mention. The initial

stages of this monograph were written at the instigation of Pat Stewart and

Richard Nowakowski. Sadly, Pat Stewart is no longer with us, and is missed

by the mathematical community. Thank you, Patrick and Richard. Finally, I

would like to thank Professor Ed Barbeau, who generously sent some of his

correspondence problems to me. His encouragement and assistance are much

appreciated.

1

An historical introduction

1.1 Preliminary remarks

In high school algebra, we learn about algebraic equations involving one or

more unknown real numbers. Functional equations are much like algebraic

equations, except that the unknown quantities are functions rather than real

numbers. This book is about functional equations: their role in contempo-

rary mathematics as well as the body of techniques that is available for their

solution. Functional equations appear quite regularly on mathematics com-

petitions. So this book is intended as a toolkit of methods for students who

wish to tackle competition problems involving functional equations at the high

school or university level.

In this chapter, we take a rather broad look at functional equations. Rather

than focusing on the solutions to such equations—a topic for later chapters—

we show how functional equations arise in mathematical investigations. Our

entry into the subject is primarily, but not solely, historical.

1.2 Nicole Oresme

Mathematicians have been working with functional equations for a much

longer period of time than the formal discipline has existed. Examples of early

functional equations can be traced back as far as the work of the fourteenth

century mathematician Nicole Oresme who provided an indirect deﬁnition

of linear functions by means of a functional equation. Of Norman heritage,

Oresme was born in 1323 and died in 1382. To put these dates in perspective,

we should note that the dreaded Black Death, which swept through Europe

killing possibly as much as a third of the population, occurred around the

middle of the fourteenth century. Although the origins of the Black Death

are unclear, we know that by December of 1347, it had reached the western

Mediterranean through the …

[PDF] Functional Equations and How to Solve Them

Functional Equations and Finite Groups of Substitutions Mihály Bessenyei

Mathematics Am. Math. Mon.

TLDR A class of functional equations is investigated, giving representations or existence theorems for the solutions, and the main tools in the proofs are Cramer’s rule and the inverse function theorem. Expand 8 Save Alert

Solving functional equations via finite substitutions Mihály Bessenyei C. Kézi

Mathematics

In this paper, we study single variable functional equations that involve one unknown function and a finite set of known functions that form a group under the operation of composition. The main … Expand 2

PDF Save Alert

Aequationes Mathematicae, to appear. SOLVING FUNCTIONAL EQUATIONS VIA FINITE SUBSTITUTIONS C. Kézi

Mathematics

In this paper, we study single variable functional equations that involve one unknown function and a finite set of known functions that form a group under the operation of composition. The main … Expand View 1 excerpt, cites background Save Alert

Testing regularity of functional equations with computer Sándor Czirbusz

Mathematics

One of the standard methods of solving functional equations is reducing the equations to a form which is easily handled by the methods of analysis, for example differential equations, partial … Expand 7 Save Alert

On a two-variable Functional Equation arising from Databases El-sayed El-hady

Mathematics

Functional equations offer a tool for narrowing the models used to describe many phenomena. Recently, a certain class of functional equations stems when obtaining the generating functions of queueing … Expand 3

PDF View 1 excerpt, cites background Save Alert

So you have finished reading the functional equations and how to solve them pdf topic article, if you find this article useful, please share it. Thank you very much. See more: Topics in functional equations PDF, Functional equation pdf, 100 functional equations Problems pdf, Awesome polynomials for mathematics competitions PDF, Function Equation Titu, 117 polynomial problems pdf, Functional equation problems, Polynomial Olympiad pdf

Top 12 Functional Equations And How To Solve Them Pdf 455 People Liked This Answer

What are the 4 types of functions in math?

What is an example of functional?

What are the 12 types of functions?

What are the 8 types of functions?

What is function explain the types of function with examples?

What is the meaning of functional equation?

What is a functional in math?

What is not a function equation?

What is function explain with example?

functional equations and how to solve them pdf

Functional Equations and How to Solve Them (Problem Books in Mathematics) by Christopher G. Small – PDF Drive

Functional Equations and How to Solve Them | SpringerLink

functional equations and how to solve them pdf

Solving Functions: Tables, Graphs, Equations (Simplifying Math) – YouTube

Solving a Functional Equation – YouTube

Problem Solving with Function Notation – YouTube

Types of Functions – Types, Definition, Examples

Functional Equations & How to Solve Them – Baixar pdf de Doceru.com

functional equations and how to solve them pdf

[PDF] Functional Equations and How to Solve Them | Semantic Scholar

functional equations and how to solve them pdf

functional equations and how to solve them pdf

(PDF) Functional Equations in Mathematical Olympiads (2017 – 2018): Problems and Solutions (Vol. I) | Amir Parvardi – Academia.edu

Functional Equations and How to Solve Them

Functional Equations & How to Solve Them

[PDF] Functional Equations and How to Solve Them

Leave a Comment Cancel reply