You are looking for information, articles, knowledge about the topic nail salons open on sunday near me how many significant figures in 400 on Google, you do not find the information you need! Here are the best content compiled and compiled by the Chewathai27.com team, along with other related topics such as: how many significant figures in 400 Significant figures, how many significant figures calculator, how many significant figures are in 450?, how many significant digits are in 23,000, Significant figures counter, Significant figures rules, 50.0 significant figures, Significant figures là gì
400. has three significant digits and is written as 4.00×102 in scientific notation.)For numbers without decimal points, trailing zeros may or may not be significant. Thus, 400 indicates only one significant figure. To indicate that the trailing zeros are significant a decimal point must be added. For example, 400. has three significant figures, and has one significant figure.The number 450 has two significant figures and would be written in scientific notation as 4.5 × 102, whereas 450.0 has four significant figures and would be written as 4.500 × 102. In scientific notation, all reported digits are significant.
| 1234 | = | 4 significant figures |
|---|---|---|
| 500 | = | 1 significant figure |
| 500. | = | 3 significant figures |
| 1300 | = | 2 significant figures |
| 2.000 | = | 4 significant figures |
Contents
Are the zeros significant in 400?
For numbers without decimal points, trailing zeros may or may not be significant. Thus, 400 indicates only one significant figure. To indicate that the trailing zeros are significant a decimal point must be added. For example, 400. has three significant figures, and has one significant figure.
How many significant figures are there in 500?
| 1234 | = | 4 significant figures |
|---|---|---|
| 500 | = | 1 significant figure |
| 500. | = | 3 significant figures |
| 1300 | = | 2 significant figures |
| 2.000 | = | 4 significant figures |
How many significant digits does 450 have?
The number 450 has two significant figures and would be written in scientific notation as 4.5 × 102, whereas 450.0 has four significant figures and would be written as 4.500 × 102. In scientific notation, all reported digits are significant.
How many significant figure are there in 200?
200 is considered to have only ONE significant figure while 25,000 has two. This is based on the way each number is written. When whole number are written as above, the zeros, BY DEFINITION, did not require a measurement decision, thus they are not significant.
How many significant figures does 405 have?
Thus, 405 g has three significant figures. Leading zeros, which are zeros at the beginning of a decimal number less than 1, are not significant.
How many significant figures are there in 300?
Example: 300 has 1 sig. fig., 25400 has 3 sig. figs.
How many significant figures does 600 have?
| Number | Scientific Notation | Significant Figures |
|---|---|---|
| 600 | 6.0×102 | 1 |
| 64.00 | 6.4×101 | 4 |
| 650 | 6.5×102 | 2 |
| 6.07×10^-15 | 6.07×10–15 | 3 |
How many significant figures are there in 1000?
so 1000. is our four-significant-figure answer. (from rules 5 and 6, we see that in order for the trailing zeros to “count” as significant, they must be followed by a decimal. Writing just “1000” would give us only one significant figure.)
How many significant figures does 890 have?
3) 890 degrees: This has two significant figures (same reason as #2) and is precise to the nearest ten grams. 4) 9010.0 grams: This has five significant figures (the final zeros are significant because there is a decimal shown) and is precise to the nearest 0.1 gram. 5) 9010.
How many significant figures does 50.0 have?
For 50: trailing zeros without implied accuracy cannot be used, so there is 1 significant figure. For 50.0: trailing zeros with implied accuracy are significant, so this value possesses 3 significant figures.
How many significant digits is 100?
100 has 1 significant figure. 4) Zeros in the beginning of a number whose only function is to place the decimal point are not significant. Example: 0.0025 has 2 significant figures.
How many significant digits does 0.091 have?
0.091 (2) Leading zeros are not significant, they are power of ten place holders. d. 0.0910 (3) Trailing zero is significant since it is written.
How many significant figures is 250?
250 The non-zeroes are significant. 250 The trailing zero is not significant (no decimal point). The number 250 has 2 significant figures.
How many significant figures are there in 205?
205 has 3 significant figures. 3. If there is a decimal point, all zeroes following non-zero numbers are significant. 2.5000 has 5 significant figures.
How many significant figures is 1400?
1400 has 2 significant figures.
How many zeros does 400 factorial have?
400 factorial has 869 digits. The number of zeros at the end is 99.
What will be the number of zeros in the square of 400?
(ii) ∵ There are 2 zeros in 400. ∴ Its square will have 4 zeros.
How many zeros are there in 500 factorial?
So the maximum possible pairs of 2 and 5 that can be made are 4 so the number of zeros in 500! are 124 . So the number of zeros in the end of the 500! are 124.
How many trailing O’s are there in the expansion of 400?
80+16+3+0=99 There are 99 zeroes at the end of 400!.… Are there any solutions to ?
how many significant figures in 400
- Article author: students.flinders.edu.au
- Reviews from users: 25434
Ratings
- Top rated: 4.7
- Lowest rated: 1
- Summary of article content: Articles about how many significant figures in 400 Updating …
- Most searched keywords: Whether you are looking for how many significant figures in 400 Updating
- Table of Contents:

Physics 1xx Laboratories: Significant figures
- Article author: courses.washington.edu
- Reviews from users: 43734
Ratings
- Top rated: 3.6
- Lowest rated: 1
- Summary of article content: Articles about Physics 1xx Laboratories: Significant figures Updating …
- Most searched keywords: Whether you are looking for Physics 1xx Laboratories: Significant figures Updating
- Table of Contents:

1.5: Expressing Numbers – Significant Figures – Chemistry LibreTexts
- Article author: chem.libretexts.org
- Reviews from users: 10737
Ratings
- Top rated: 3.8
- Lowest rated: 1
- Summary of article content: Articles about 1.5: Expressing Numbers – Significant Figures – Chemistry LibreTexts Updating …
- Most searched keywords: Whether you are looking for 1.5: Expressing Numbers – Significant Figures – Chemistry LibreTexts Updating Significant figures properly report the number of measured and estimated digits in a measurement. There are rules for applying significant figures in calculations.
- Table of Contents:
Rounding off numbers
Combining Numbers
Concept Review Exercises
Answers
Key Takeaways

how many significant figures in 400
- Article author: www.ruf.rice.edu
- Reviews from users: 40981
Ratings
- Top rated: 4.2
- Lowest rated: 1
- Summary of article content: Articles about how many significant figures in 400 Updating …
- Most searched keywords: Whether you are looking for how many significant figures in 400 Updating
- Table of Contents:

how many significant figures in 400
- Article author: www.chemicalaid.com
- Reviews from users: 787
Ratings
- Top rated: 3.1
- Lowest rated: 1
- Summary of article content: Articles about how many significant figures in 400 Sig fig calculator with steps: 400. has 3 significant figures and 0 decimals. …
- Most searched keywords: Whether you are looking for how many significant figures in 400 Sig fig calculator with steps: 400. has 3 significant figures and 0 decimals.
- Table of Contents:

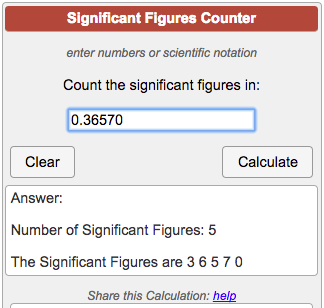
Significant Figures Counter
- Article author: www.calculatorsoup.com
- Reviews from users: 15126
Ratings
- Top rated: 5.0
- Lowest rated: 1
- Summary of article content: Articles about Significant Figures Counter Count how many significant figures are in a number, and find which digits are significant. You can use this calculator for significant figures practice: … …
- Most searched keywords: Whether you are looking for Significant Figures Counter Count how many significant figures are in a number, and find which digits are significant. You can use this calculator for significant figures practice: … Count how many significant figures in a number. Learn how to count sig figs in numbers, decimal numbers and scientific notation. Rules for significant digits.significant figures, round, significant digits, sig fig
- Table of Contents:
Calculator Use
Find How Many Significant Figures
How to Identify Non-Significant Figures
Related Calculators
How many significant figures are in 400?
- Article author: clickcalculators.com
- Reviews from users: 39109
Ratings
- Top rated: 3.6
- Lowest rated: 1
- Summary of article content: Articles about How many significant figures are in 400? The answer is: The number of significant figures in 400 is 1. Significant figures definitions. We use in this calculator the following concepts: Leading zeros … …
- Most searched keywords: Whether you are looking for How many significant figures are in 400? The answer is: The number of significant figures in 400 is 1. Significant figures definitions. We use in this calculator the following concepts: Leading zeros …
- Table of Contents:
Significant Figures or Digits Calculator
Significant figures definitions
Significant figures rules
Significant figures or digits counting examples

The number of significant figures in 0.400 is
- Article author: www.doubtnut.com
- Reviews from users: 9854
Ratings
- Top rated: 3.9
- Lowest rated: 1
- Summary of article content: Articles about The number of significant figures in 0.400 is Get Answer to any question, just click a photo and upload the photo and get the answer completely free,. UPLOAD PHOTO AND GET THE ANSWER NOW … …
- Most searched keywords: Whether you are looking for The number of significant figures in 0.400 is Get Answer to any question, just click a photo and upload the photo and get the answer completely free,. UPLOAD PHOTO AND GET THE ANSWER NOW … The number of significant figures in 0.400 is
- Table of Contents:

See more articles in the same category here: Top 975 tips update new.
Rules for Significant Figures
Significant Figures
The significant figures of a (measured or calculated) quantity are the meaningful digits in it. There are conventions which you should learn and follow for how to express numbers so as to properly indicate their significant figures.
Any digit that is not zero is significant. Thus 642 has three significant figures and 6.792 has four significant figures.
Zeros between non zero digits are significant. Thus 4023 has four significant figures.
Zeros to the left of the first non zero digit are not significant. Thus 0.000072 has only two significant figures. This is more easily seen if it is written as 7.2 x10 -5 .
. For numbers with decimal points, zeros to the right of a non zero digit are significant. Thus 6.00 has three significant figures and 0.050 has two significant figures. For this reason it is important to keep the trailing zeros to indicate the actual number of significant figures.
For numbers without decimal points, trailing zeros may or may not be significant. Thus, 400 indicates only one significant figure. To indicate that the trailing zeros are significant a decimal point must be added. For example, 400. has three significant figures, and has one significant figure.
Exact numbers have an infinite number of significant digits. For example, if there are two oranges on a table, then the number of oranges is 2.000… . Defined numbers are also like this. For example, the number of centimeters per inch (2.54) has an infinite number of significant digits, as does the speed of light (299792458 m/s).
There are also specific rules for how to consistently express the uncertainty associated with a number. In general, the last significant figure in any result should be of the same order of magnitude (i.e.. in the same decimal position) as the uncertainty. Also, the uncertainty should be rounded to one or two significant figures. Always work out the uncertainty after finding the number of significant figures for the actual measurement.
For example:
9.82 ± 0.02
10.0 ± 1.5
4 ± 1
The following numbers are all incorrect.
9.82 ± 0.02385 is wrong but 9.82 ± 0.02 is fine
10.0 ± 2 is wrong but 10.0 ± 2.0 is fine
4 ± 0.5 is wrong but 4.0 ± 0.5 is fine
In practice, when doing mathematical calculations, it is a good idea to keep one more digit than is significant to reduce rounding errors. But in the end, the answer must be expressed with only the proper number of significant figures. After addition or subtraction, the result is significant only to the place determined by the largest last significant place in the original numbers. For example,
89.332 + 1.1 = 90.432
should be rounded to get 90.4 (the tenths place is the last significant place in 1.1). After multiplication or division, the number of significant figures in the result is determined by the original number with the smallest number of significant figures. For example,
(2.80) (4.5039) = 12.61092
should be rounded off to 12.6 (three significant figures like 2.80).
Physics 1xx Laboratories: Significant figures
Physics 1xx Laboratories – Web Assign
Significant Figures on WebAssign
How does sig figs checking work?
Sig figs checking on a computer is very strict. Remember these rules regarding sig figs:
The leftmost nonzero digit is the most significant digit. If there is no decimal point, the rightmost nonzero digit is the least significant digit. If there is a decimal point, the rightmost digit is the least significant digit, even if it is a 0. All digits between the least and most significant digits are counted as significant.
When using scientific notation, enter the number using the “e” notation. For example, a value of 1.3×10−2 would be entered in WebAssign as “1.3e-2”. Note: The “e” must be lower case.
Here are some examples:
1234 = 4 significant figures 5.0e2 = 2 significant figures 500 = 1 significant figure 140e-001 = 2 significant figures 500. = 3 significant figures 8.20000e3 = 6 significant figures 1300 = 2 significant figures 101.001e2 = 6 significant figures 2.000 = 4 significant figures 41003 = 5 significant figures
To express a number like 1000 to 2 or 3 significant figures, you need to use scientific notation, for example, “1.00e3” would give you 3 significant figures.
Do all numerical questions check significant figures?
No. Much of the time, the questions that do check for sig figs show a little sig-fig icon (a 4.0 with a check-mark next to it). If you see this, then the sig figs are definitely checked. If you do not see it, they may be checked on the first submission, or not. It depends on the question coding.
If my answer is marked wrong, is it because the significant figures are wrong?
Mostly, no. Unless you actually see a red hint telling you that the significant figures are incorrect, then the reason for your answer being marked wrong has nothing to do with sig figs. What it means is that your submission is outside of the acceptable tolerance for being marked correct. In other words, you have a bigger problem than sig figs. Do not mess with the sig figs of your answer unless you see the hint.
What is the relationship between the “tolerance” and the number of sig figs?
The “tolerance” is the range of numbers that WebAssign will mark as correct. The tolerance can be set by the problem coder to just about anything. But by default, the tolerance is 2% of the “key”. The “key” is the exactly correct value. For example, if the key were “9.81 m/s^2”, with a tolerance of 2%, then any entry between “9.6138 m/s^2” and “10.0062 m/s^2” would be counted as correct. This is if there is no sig figs checking.
If sig figs are being checked, then in the question coding there is a variable called $SIGFIGS that is set to a number greater than 0. That number determines how many significant figures there must be in order for the question to be marked correct. By default, any entry that does not have exactly that number of sig figs will be marked totally wrong (0 points awarded), regardless of the value of the number.
If sig figs checking is used, the default tolerance is not a certain percent of the key but is instead usually 1 of the least significant digits. For example, if, in the previous problem, $SIGFIGS was set to 3, then the tolerance would be set to allow answers between 9.80 m/s^2 and 9.83 m/s^2.
However, both the value of $SIGFIGS and the tolerance can be altered by the question coding; this means it can change within a single problem depending on how the question was written. In many lab-related questions, $SIGFIGS is allowed to be set to a range of values, say between 1 and 4. The point is to make the question accept up to a certain maximum number of figures. As the $SIGFIGS value changes depending on what is entered, the tolerance also changes.
Sig figs in numbers with uncertainty
When a value is reported with an uncertainty, special rules apply. The uncertainty can affect the required number of significant figures in the value. A large uncertainty may require that the value be rounded to fewer figures, and a very small uncertainty may imply that the value be known to a greater number of figures. In addition, the uncertainty itself cannot have an arbitrary number of significant figures.
A number that is to be used as an uncertainty itself is fundamentally an estimate: uncertainty cannot be known precisely. Thus, by convention, you must never use more than 2 significant figures to state it.
Remember these two rules for stating a number with an uncertainty: (1) The uncertainty should be stated with 1 or 2 significant figures. (2) A value and its uncertainty should be stated to the same precision: they should have the same number of digits past the decimal point. Usually, if the leading nonzero digit in the uncertainty is greater than one, there should be only one significant digit in the uncertainty. But, if the leading digit is a 1, there may be 2 significant digits in the uncertainty. Units should always be written after the uncertainty. Note the following examples:
Example Comment 2.67±0.03 m/s2 OK 2.7±0.3 m/s2 OK 2.67±0.13 m/s2 OK (note leading “1” in uncertainty) 2.672±0.016 m/s2 OK 2.67±0.0162 m/s2 Not OK, too many digits in uncertanty. 2.67342±0.02 m/s2 Not OK, too many digits in value. 2.7±0.32 m/s2 Not OK, too many digits in uncertainty or too few in value. 2.67±0.3 m/s2 Not OK, too many digits in value or too few in uncertainty. 2.60e2±0.02 m/s2 Not OK, too few digits in value. 2.6000e2±0.02 m/s2 OK, both numbers stated to same precision.
Because the value and uncertainty must be stated to the same precision, it may require either adjusting the value or the uncertainty to make the precision match. For example “1.56±0.028 N” would be incorrect, but either “1.56±0.03 N” or “1.558±0.028 N” would be correct, assuming both values are within tolerance of their respective keys.
Note however with 2 digits, the associated value must be stated to a greater precision in order to fall within a tighter tolerance. For example, if the key for an uncertainty were “0.028 kg*m/s”, then “0.03 kg*m/s” would be accepted, but “0.030 kg*m/s” would not be accepted.
When no uncertainty is stated, the uncertainty of an experimental number is implied by the number of significant figures used to represent it. Take the value 9.81 m/s2. That there are three significant figures implies a real distinction between “9.81” and “9.82” m/s2. Given no other information, you must assume that the uncertainty in the number is 0.005 m/s2 (even though the default WebAssign tolerance would allow for a greater range of answers).
This is too much to keep track of. Tell me what I should DO!
Assume all tolerances are 1%, regardless of sig figs. If you are allowed multiple submissions, enter 1 or 2 more sig figs that you think you should. If you get the question marked wrong , but do not see a sig figs hint , (or see a hint like Incorrect number ) then you are outside of tolerance, regardless of the number of figures. Recalculate your answer from scratch, keeping all intermediate values you may have needed, to as many figures as possible. If you get the question marked wrong AND you ONLY see the sig figs hint , then the ONLY thing wrong is the number of significant figures. You will probably need to round to fewer if you have more than 4 figures in your submission, or extend out to more figures if you have less than 1 or 2 (although there are some that take only one sig fig). When stating numbers with uncertainty, you may need more figures rather than fewer.
ADVICE: Always fill in all blanks to a multi-part question.
Because sig figs in an answer may depend on the value of the uncertainty, it is important that these numbers be there for the program to work. If you see odd behavior, like a previously “correct” entry becoming “incorrect”, it is almost certanly due to the fact that a later entry is being used to check an earlier one. In general, WebAssign questions are designed to work by reading all of the entries. Think through the whole problem, not just one number at a time.
1.5: Expressing Numbers – Significant Figures
Learning Objectives Understand the importance of significant figures in measured numbers.
Identify the number of significant figures in a reported value.
Use significant figures correctly in arithmetical operations.
Scientists have established certain conventions for communicating the degree of precision of a measurement, which is dependent on the measuring device used. Imagine, for example, that you are using a meterstick to measure the width of a table. The centimeters (cm) marked on the meterstick, tell you how many centimeters wide the table is. Many metersticks also have markings for millimeters (mm), so we can measure the table to the nearest millimeter. Most metersticks do not have any smaller (or more precise) markings indicated, so you cannot report the measured width of the table any more precise than to the nearest millimeter. However, you can estimate one past the smallest marking, in this case the millimeter, to the next decimal place in the measurement (Figure \(\PageIndex{1}\)).
Figure \(\PageIndex{1}\): Measuring an Object to the Correct Number of Digits. How many digits should be reported for the length of this object?
The concept of significant figures takes this limitation into account. The significant figures of a measured quantity are defined as all the digits known with certainty (those indicated by the markings on the measuring device) and the first uncertain, or estimated, digit (one digit past the smallest marking on the measuring device). It makes no sense to report any digits after the first uncertain one, so it is the last digit reported in a measurement. Zeros are used when needed to place the significant figures in their correct positions. Thus, zeros are sometimes counted as significant figures but are sometimes only used as placeholders.
“Sig figs” is a common abbreviation for significant figures.
Consider the earlier example of measuring the width of a table with a meterstick. If the table is measured and reported as being 1,357 mm wide, the number 1,357 has four significant figures. The 1 (thousands place), the 3 (hundreds place), and the 5 (tens place) are certain; the 7 (ones place) is assumed to have been estimated. It would make no sense to report such a measurement as 1,357.0 (five Sig Figs) or 1,357.00 (six Sig Figs) because that would suggest the measuring device was able to determine the width to the nearest tenth or hundredth of a millimeter, when in fact it shows only tens of millimeters and therefore the ones place was estimated.
On the other hand, if a measurement is reported as 150 mm, the 1 (hundreds) and the 5 (tens) are known to be significant, but how do we know whether the zero is or is not significant? The measuring device could have had marks indicating every 100 mm or marks indicating every 10 mm. How can you determine if the zero is significant (the estimated digit), or if the 5 is significant and the zero a value placeholder?
The rules for deciding which digits in a measurement are significant are as follows:
All nonzero digits are significant. In 1,357 mm, all the digits are significant. Sandwiched (or embedded) zeros, those between significant digits, are significant. Thus, 405 g has three significant figures. Leading zeros, which are zeros at the beginning of a decimal number less than 1, are not significant. In 0.000458 mL, the first four digits are leading zeros and are not significant. The zeros serve only to put the digits 4, 5, and 8 in the correct decimal positions. This number has three significant figures. Trailing zeros, which are zeros at the end of a number, are significant only if the number has a decimal point. Thus, in 1,500 m, the two trailing zeros are not significant because the number is written without a decimal point; the number has two significant figures. However, in 1,500.00 m, all six digits are significant because the number has a decimal point.
Example \(\PageIndex{1}\) How many significant figures does each number have? 6,798,000 6,000,798 6,000,798.00 0.0006798 Answer a four (by rules 1 and 4) Answer b seven (by rules 1 and 2) Answer c nine (by rules 1, 2, and 4) Answer d four (by rules 1 and 3)
Exercise \(\PageIndex{1}\) How many significant figures does each number have? 2.1828 0.005505 55,050 5 500 Answer a five Answer b four Answer c four Answer d one Answer e one
Rounding off numbers Before dealing with the specifics of the rules for determining the significant figures in a calculated result, we need to be able to round numbers correctly. To round a number, first decide how many significant figures the number should have. Once you know that, round to that many digits, starting from the left. If the number immediately to the right of the last significant digit is less than 5, it is dropped and the value of the last significant digit remains the same. If the number immediately to the right of the last significant digit is greater than or equal to 5, the last significant digit is increased by 1. Consider the measurement 207.518m. Right now, the measurement contains six significant figures. How would we successively round it to fewer and fewer significant figures? Follow the process as outlined in Table 1.5.1. Number of Significant Figures Rounded Value Reasoning Table 1.5.1: Rounding examples 6 207.518 All digits are significant 5 207.52 8 rounds the 1 up to 2 4 207.5 2 is dropped 3 208 5 rounds the 7 up to 8 2 210 8 is replaced by a 0 and rounds the 0 up to 1 1 200 1 is replaced by a 0 Notice that the more rounding that is done, the less reliable the figure is. An approximate value may be sufficient for some purposes, but scientific work requires a much higher level of detail. It is important to be aware of significant figures when you are mathematically manipulating numbers. For example, dividing 125 by 307 on a calculator gives 0.4071661238… to an infinite number of digits. But do the digits in this answer have any practical meaning, especially when you are starting with numbers that have only three significant figures each? When performing mathematical operations, there are two rules for limiting the number of significant figures in an answer—one rule is for addition and subtraction, and one rule is for multiplication and division. In operations involving significant figures, the answer is reported in such a way that it reflects the reliability of the least precise operation. An answer is no more precise than the least precise number used to get the answer.
Combining Numbers For addition or subtraction, the rule is to stack all the numbers with their decimal points aligned and then limit (round to) the answer’s significant figures to the rightmost column for which all the numbers have significant figures. Consider the following: The arrow points to the rightmost column in which all the numbers have significant figures—in this case, the tenths place. Therefore, we will limit our final answer to the tenths place. Is our final answer therefore 1,459.0? No, because when we drop digits from the end of a number, we also have to round the number. Notice that the first dropped digit, in the hundredths place, is 8. This suggests that the answer is actually closer to 1,459.1 than it is to 1,459.0, so we need to round up to 1,459.1. The standard rules for rounding numbers are simple: If the first dropped digit is 5 or higher, round up. If the first dropped digit is lower than 5, do not round up. For multiplication or division, the rule is to count the number of significant figures in each number being multiplied or divided and then limit the significant figures in the answer to the lowest count. An example is as follows: The final answer, limited to four significant figures, is 4,094. The first digit dropped is 1, so we do not round up. Scientific notation provides a way of communicating significant figures without ambiguity. You simply include all the significant figures in the leading number. For example, the number 4,000 has one significant figure and should be written as the number 4 × 104. The number 450 has two significant figures and would be written in scientific notation as 4.5 × 102, whereas 450.0 has four significant figures and would be written as 4.500 × 102. In scientific notation, all reported digits are significant. Example \(\PageIndex{2}\) Write the answer for each expression using scientific notation with the appropriate number of significant figures. 23.096 × 90.300 125 × 9.000 1,027 + 610.0 + 363.06 Answer a The calculator answer is 2,085.5688, but we need to round it to five significant figures. Because the first digit to be dropped (in the hundredths place) is greater than 5, we round up to 2,085.6, which in scientific notation is 2.0856 × 103. Answer b The calculator gives 1,125 as the answer, but we limit it to three significant figures and convert into scientific notation: 1.13 × 103. Answer c The calculator gives 2,000.06 as the answer, but because 1,027 has its farthest-right significant figure in the ones column, our answer must be limited to the ones position: 2,000 which in scientific notation is 2.000 × 103. Exercise \(\PageIndex{2}\) Write the answer for each expression using scientific notation with the appropriate number of significant figures. 217 ÷ 903 13.77 + 908.226 + 515 255.0 − 99 0.00666 × 321 Answer a 0.240 = 2.40 x 10-1 Answer b 1437 = 1.437 x 103 Answer c 156 = 1.56 x 102 Answer d 2.14 = 2.14 x 100 Remember that calculators do not understand significant figures. You are the one who must apply the rules of significant figures to a result from your calculator.
Concept Review Exercises Explain why the concept of significant figures is important in scientific measurements. State the rules for determining the significant figures in a measurement. When do you round a number up, and when do you not round a number up?
Answers Significant figures represent all the known digits of a measurement plus the first estimated one. It gives information about how precise the measuring device and measurement is. All nonzero digits are significant; zeros between nonzero digits are significant; zeros at the end of a nondecimal number or the beginning of a decimal number are not significant; zeros at the end of a decimal number are significant. Round up only if the first digit dropped is 5 or higher.
So you have finished reading the how many significant figures in 400 topic article, if you find this article useful, please share it. Thank you very much. See more: Significant figures, how many significant figures calculator, how many significant figures are in 450?, how many significant digits are in 23,000, Significant figures counter, Significant figures rules, 50.0 significant figures, Significant figures là gì

