Top 28 How Many Skew Lines Are In A Rectangular Prism 10143 Good Rating This Answer

You are looking for information, articles, knowledge about the topic nail salons open on sunday near me how many skew lines are in a rectangular prism on Google, you do not find the information you need! Here are the best content compiled and compiled by the Chewathai27.com team, along with other related topics such as: how many skew lines are in a rectangular prism how many pairs of skew lines are in a cube, how many parallel lines in a square, how many parallel lines are in a rectangular prism, how many parallel lines in a trapezium, how many parallel lines in a rectangle, how many parallel lines in a triangle, how many parallel lines does a parallelogram have, how many parallel lines does a rhombus have

Contents

What are skew lines in a rectangular prism?

(Two lines are skew lines when they do not intersect and are not coplanar.) Think of each segment in the figure as part of a line. Which line(s) or plane(s) appear to fit the description? 1.

How many skewed lines are in a cube?

In the cube shown, and are examples of two lines that are skew. You can verify this by checking the conditions for skew lines. and do not intersect.

Can you have 3 skew lines?

Since two lines in the plane must intersect or be parallel, skew lines can exist only in three or more dimensions.

How do you find skew lines?

Step 1: Find lines that do not intersect each other. Step 2: Check if these pairs of lines are also not parallel to each other. Step 3: Next, check if these non-intersecting and non-parallel lines are non-coplanar. If yes then the chosen pair of lines are skew lines.

What is meant by skew lines?

Definition of skew lines

: straight lines that do not intersect and are not in the same plane.

What is skew lines in graph?

Skew lines are lines that are in different planes, they are never parallel, and they never intersect. On the other hand, parallel lines are lines that are in the same plane and never intersect.

Are skew lines in the same plane?

Skew lines are never in the same plane. Skew lines can be perpendicular. Planes can be parallel.

What are skew lines 3d geometry?

In three-dimensional geometry, skew lines are two lines that do not intersect and are not parallel. A simple example of a pair of skew lines is the pair of lines through opposite edges of a regular tetrahedron.

How do you find skew lines in 3d?

The (shortest) distance between a pair of skew lines can be found by obtaining the length of the line segment that meets perpendicularly with both lines, which is d d d in the figure below. Find the distance between the following pair of skew lines: x = − y + 2 = − z + 2 and x − 2 = − y + 1 = z + 1.

What is skew lines in graph?

Skew lines are lines that are in different planes, they are never parallel, and they never intersect. On the other hand, parallel lines are lines that are in the same plane and never intersect.

Which are skew lines A and B?

Skew lines are noncoplanar and do not intersect. Line a lies in plane Q and line b lies in plane R, so the lines are not coplanar. No other plane can be drawn through the lines, so they are not parallel. So, a and b are skew.

Are skew lines in the same plane?

Skew lines are never in the same plane. Skew lines can be perpendicular. Planes can be parallel.

Can skew lines have a point in common?

Skew lines are lines that do not intersect, and there is no plane that contains them. Intersecting lines are two coplanar lines with exactly one point in common. Concurrent lines are lines that contain the same point. Two distinct coplanar lines m and n that have no points in common are parallel lines.

Skew Lines, Perpendicular Parallel Lines Planes, Intersecting Lines Transversals

geometry – Pairs of skew lines of a cube – Mathematics Stack Exchange

Article author: math.stackexchange.com
Reviews from users: 22010 Ratings
Top rated: 4.0
Lowest rated: 1
Summary of article content: Articles about geometry – Pairs of skew lines of a cube – Mathematics Stack Exchange A simpler explanation is that there are five skew lines for each diagonal since there is one on each other face. – user381493. …
Most searched keywords: Whether you are looking for geometry – Pairs of skew lines of a cube – Mathematics Stack Exchange A simpler explanation is that there are five skew lines for each diagonal since there is one on each other face. – user381493.
Table of Contents:

1 Answer
1

Your Answer

Not the answer you’re looking for Browse other questions tagged geometry 3d or ask your own question

$geometry - Pairs of skew lines of a cube - Mathematics Stack Exchange$

geometry – Pairs of skew lines of a cube – Mathematics Stack Exchange

Article author: benson.k12.mn.us
Reviews from users: 42692 Ratings
Top rated: 3.6
Lowest rated: 1
Summary of article content: Articles about how many skew lines are in a rectangular prism Updating …
Most searched keywords: Whether you are looking for how many skew lines are in a rectangular prism Updating
Table of Contents:

how many skew lines are in a rectangular prism

Article author: www.storyofmathematics.com
Reviews from users: 5794 Ratings
Top rated: 3.6
Lowest rated: 1
Summary of article content: Articles about Skew lines – Explanation & Examples Updating …
Most searched keywords: Whether you are looking for Skew lines – Explanation & Examples Updating Skew lines are lines that do not lie in the same plane and are neither parallel nor intersecting. Learn more about skew lines here!
Table of Contents:

What are skew lines

How to find skew lines

Article author: mathworld.wolfram.com
Reviews from users: 4635 Ratings
Top rated: 3.5
Lowest rated: 1
Summary of article content: Articles about Skew Lines — from Wolfram MathWorld Updating …
Most searched keywords: Whether you are looking for Skew Lines — from Wolfram MathWorld Updating Two or more lines which have no intersections but are not parallel, also called agonic lines. Since two lines in the plane must intersect or be parallel, skew lines can exist only in three or more dimensions. Two lines with equations x = x_1+(x_2-x_1)s (1) x = x_3+(x_4-x_3)t (2) are skew if (x_1-x_3)·[(x_2-x_1)x(x_4-x_3)]!=0 (3) (Gellert et al. 1989, p. 539). This is equivalent to the statement that the vertices of the lines are not coplanar, i.e., |x_1 y_1 z_1 1; x_2 y_2 z_2 1;…
Table of Contents:

Skew lines – Explanation & Examples

Skew Lines – Explanation & Examples

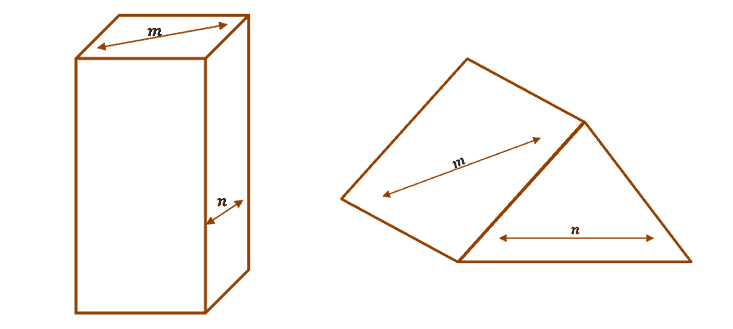
What are skew lines? How do we identify a pair of skew lines? Let’s start with a brief definition of skew lines:

Skew lines are two or more lines that are not: intersecting, parallel, and coplanar with respect to each other.

For us to understand what skew lines are, we need to review the definitions of the following terms:

Parallel Lines – these are lines that lie on the same plane but never meet.

Intersecting Lines – these are lines that lie on the same plane and meet.

Coplanar Lines – these are lines that lie on the same plane.

What if we have lines that do not meet these definitions? This is why we need to learn about skew lines.

In this article, you will learn what skew lines are, how to find skew lines, and determine whether two given lines are skewed.

What are skew lines?

Skew lines are two or more lines that do not intersect, are not parallel, and are not coplanar. (Remember that parallel lines and intersecting lines lie on the same plane.)

This makes skew lines unique – you can only find skew lines in figures with three or more dimensions.

The lines $m$ and $n$ are examples of two skew lines for each figure. You can know right away by seeing how they lie on different surfaces and positioned so that they are not parallel or intersecting.

What are real-world examples of skew lines?

Since skew lines are found in three or more dimensions, our world will definitely contain skew lines. Here are some examples to help you better visualize skew lines:

The lines found on the walls and the ceiling’s respective surfaces. Since the lines on each of the surfaces are in different planes, the lines within each of the surfaces will never meet, nor will they be parallel.

Two or more street signs lying along with the same post. The lines in each street sign are not in the same plane, and they are neither intersecting nor parallel to each other.

Roads along highways and overpasses in a city. Since the roads are considered as separate planes, lines found in each will never intersect nor are parallel to each other.

How to find skew lines?

When given a figure or real-world examples, to find a pair of skew lines, always go back to the definition of skew lines. Ask the following questions:

What are the lines (in the figure) that do not intersect each other?

Are the chosen lines not found lying on the same plane?

Are the chosen lines not parallel to each other?

If the answers to the three questions are YES, then you have found a pair of two lines.

In the cube shown, $AB$ and $EH$ are examples of two lines that are skew. You can verify this by checking the conditions for skew lines.

$AB$ and $EH$ do not intersect.

$AB$ and $EH$ do not lie on the same plane.

$AB$ and $EH$ are not parallel.

This confirms that the two are skew with respect to each other.

What are other skew lines’ definitions?

We have discussed how to find skew lines from figures in the previous sections. Now, we can take a quick look into another definition of skew lines in higher mathematics.

Given two equations in vector form as shown:

$\boldsymbol{x} = \boldsymbol{x_1 }+( \boldsymbol{x_2 }- \boldsymbol{x_1})a$

$\boldsymbol{x} = \boldsymbol{x_3 }+( \boldsymbol{x_4 }- \boldsymbol{x_3})a$

They are skew lines only when $(\boldsymbol{x_1x_3})[(\boldsymbol{x_2}- \boldsymbol{x_1})(\boldsymbol{x_4}-\boldsymbol{x_3})]$ is not equal to zero.

We won’t use this definition of skew lines in a precalculus class, so for now, we can look through the equations briefly and focus on the geometrical concept of skew lines.

Example 1

Which of the following figures will you be able to find skew lines? Hexagon Cube The surface of a Sphere Octagon

Solution

By definition, we can only find skew lines in figures with three or more dimensions. Planes can never contain skew lines, so (a), (c), and (d) are no longer valid options.

Cubes are three-dimensional and can contain skew lines. So, it’s b.

Example 2

Which of the following examples are best represented by skew lines?

The length and width of a rectangular lot. The two hands of a clock. A southbound subway and a westbound highway. The equator of the earth.

Solution

Start by eliminating options that are not skew lines:

Which of these do not lie on the same plane? The rectangular plot (a).

Which of these four examples do not intersect? The two hands of the clock (b).

We’re left with c and d, but the earth’s equator is just one straight line revolving around the globe. That only leaves us with c.

To confirm: a subway heading southbound and a westbound highway lie on two different roads (or planes). They will never intersect, nor are they parallel, so the two are skew lines.

Example 3

Fill in the sentences shown below with parallel, intersecting, or skew.

The hour hand and minute hand of a clock are _______ each other.

The vertical strings of a tennis racket are ________ to each other.

The curtain pole along the window panes and the line along the ceiling are ______ with respect to each other.

Solution

The two hands of the clock are connected at the center. This means that the two are intersecting each other.

each other. The vertical strings are lying along the same plane and direction, so they are parallel .

. The curtain pole and the line are in two different planes and will never intersect, so they are skewed with respect to each other.

Example 4

True or False? The strings along a tennis racket’s nets are considered skew to each other.

Solution

False. Since a tennis racket’s surface is considered one plane, all the strings (or the lines) found are coplanar. This means that none of them can ever be skew to each other.

Example 5

Take a screenshot or snip the image below and sketch two pairs of skew lines.

Solution

This question can have multiple possible solutions. Make use of the skew lines’ definition. Below are three possible pairs of skew lines.

As shown in the three examples, as long as the lines are not coplanar, do not intersect, and are not parallel, they can be considered skew lines.

Example 6

Take a screenshot or snip the image below and sketch one line that will still be skew with the two other lines.

Solution

Look for a third segment in the figure above that does not lie on the same planes as the two given lines.

This problem has multiple possible answers. As long as the third line remains skewed with the two given lines, the answer is valid.

Example 7

Aside from AB and EH, name two other pairs of skew lines in the cube shown.

Solution

Look for two segments in the cube that do not lie on the same plane and do not intersect.

Other examples of skew lines are: $AC$ and $DH$, $AF$ and $GH$, and $BE$ and $CG$.

There can be more variations as long as the lines meet the definition of skew lines.

Example 8

Identify three pairs of skew lines in the figure shown below.

Solution

Look for three pairs of segments in the figure above that do not lie on the same plane, are not parallel, and do not intersect.

Three possible pairs of skew lines are: $AI$ and $DE$, $FE$ and $IC$, as well as $BC$ and $GF$.

This problem has multiple possible answers. As long as the lines meet the definition of skew lines, the three pairs will be valid.

Skew Lines — from Wolfram MathWorld

Two or more lines which have no intersections but are not parallel, also called agonic lines. Since two lines in the plane must intersect or be parallel, skew lines can exist only in three or more dimensions.

Two lines with equations

(1) (2)

are skew if

(3)

(Gellert et al. 1989, p. 539).

This is equivalent to the statement that the vertices of the lines are not coplanar, i.e.,

(4)

Three skew lines always define a one-sheeted hyperboloid, except in the case where they are all parallel to a single plane but not to each other. In this case, they determine a hyperbolic paraboloid (Hilbert and Cohn-Vossen 1999, p. 15).

Skew lines – Explanation & Examples

Skew Lines – Explanation & Examples

What are skew lines? How do we identify a pair of skew lines? Let’s start with a brief definition of skew lines:

Skew lines are two or more lines that are not: intersecting, parallel, and coplanar with respect to each other.

For us to understand what skew lines are, we need to review the definitions of the following terms:

Parallel Lines – these are lines that lie on the same plane but never meet.

Intersecting Lines – these are lines that lie on the same plane and meet.

Coplanar Lines – these are lines that lie on the same plane.

What if we have lines that do not meet these definitions? This is why we need to learn about skew lines.

In this article, you will learn what skew lines are, how to find skew lines, and determine whether two given lines are skewed.

What are skew lines?

Skew lines are two or more lines that do not intersect, are not parallel, and are not coplanar. (Remember that parallel lines and intersecting lines lie on the same plane.)

This makes skew lines unique – you can only find skew lines in figures with three or more dimensions.

The lines $m$ and $n$ are examples of two skew lines for each figure. You can know right away by seeing how they lie on different surfaces and positioned so that they are not parallel or intersecting.

What are real-world examples of skew lines?

Since skew lines are found in three or more dimensions, our world will definitely contain skew lines. Here are some examples to help you better visualize skew lines:

The lines found on the walls and the ceiling’s respective surfaces. Since the lines on each of the surfaces are in different planes, the lines within each of the surfaces will never meet, nor will they be parallel.

Two or more street signs lying along with the same post. The lines in each street sign are not in the same plane, and they are neither intersecting nor parallel to each other.

Roads along highways and overpasses in a city. Since the roads are considered as separate planes, lines found in each will never intersect nor are parallel to each other.

How to find skew lines?

When given a figure or real-world examples, to find a pair of skew lines, always go back to the definition of skew lines. Ask the following questions:

What are the lines (in the figure) that do not intersect each other?

Are the chosen lines not found lying on the same plane?

Are the chosen lines not parallel to each other?

If the answers to the three questions are YES, then you have found a pair of two lines.

In the cube shown, $AB$ and $EH$ are examples of two lines that are skew. You can verify this by checking the conditions for skew lines.

$AB$ and $EH$ do not intersect.

$AB$ and $EH$ do not lie on the same plane.

$AB$ and $EH$ are not parallel.

This confirms that the two are skew with respect to each other.

What are other skew lines’ definitions?

We have discussed how to find skew lines from figures in the previous sections. Now, we can take a quick look into another definition of skew lines in higher mathematics.

Given two equations in vector form as shown:

$\boldsymbol{x} = \boldsymbol{x_1 }+( \boldsymbol{x_2 }- \boldsymbol{x_1})a$

$\boldsymbol{x} = \boldsymbol{x_3 }+( \boldsymbol{x_4 }- \boldsymbol{x_3})a$

They are skew lines only when $(\boldsymbol{x_1x_3})[(\boldsymbol{x_2}- \boldsymbol{x_1})(\boldsymbol{x_4}-\boldsymbol{x_3})]$ is not equal to zero.

We won’t use this definition of skew lines in a precalculus class, so for now, we can look through the equations briefly and focus on the geometrical concept of skew lines.

Example 1

Which of the following figures will you be able to find skew lines? Hexagon Cube The surface of a Sphere Octagon

Solution

By definition, we can only find skew lines in figures with three or more dimensions. Planes can never contain skew lines, so (a), (c), and (d) are no longer valid options.

Cubes are three-dimensional and can contain skew lines. So, it’s b.

Example 2

Which of the following examples are best represented by skew lines?

The length and width of a rectangular lot. The two hands of a clock. A southbound subway and a westbound highway. The equator of the earth.

Solution

Start by eliminating options that are not skew lines:

Which of these do not lie on the same plane? The rectangular plot (a).

Which of these four examples do not intersect? The two hands of the clock (b).

We’re left with c and d, but the earth’s equator is just one straight line revolving around the globe. That only leaves us with c.

To confirm: a subway heading southbound and a westbound highway lie on two different roads (or planes). They will never intersect, nor are they parallel, so the two are skew lines.

Example 3

Fill in the sentences shown below with parallel, intersecting, or skew.

The hour hand and minute hand of a clock are _______ each other.

The vertical strings of a tennis racket are ________ to each other.

The curtain pole along the window panes and the line along the ceiling are ______ with respect to each other.

Solution

The two hands of the clock are connected at the center. This means that the two are intersecting each other.

each other. The vertical strings are lying along the same plane and direction, so they are parallel .

. The curtain pole and the line are in two different planes and will never intersect, so they are skewed with respect to each other.

Example 4

True or False? The strings along a tennis racket’s nets are considered skew to each other.

Solution

False. Since a tennis racket’s surface is considered one plane, all the strings (or the lines) found are coplanar. This means that none of them can ever be skew to each other.

Example 5

Take a screenshot or snip the image below and sketch two pairs of skew lines.

Solution

This question can have multiple possible solutions. Make use of the skew lines’ definition. Below are three possible pairs of skew lines.

As shown in the three examples, as long as the lines are not coplanar, do not intersect, and are not parallel, they can be considered skew lines.

Example 6

Take a screenshot or snip the image below and sketch one line that will still be skew with the two other lines.

Solution

Look for a third segment in the figure above that does not lie on the same planes as the two given lines.

This problem has multiple possible answers. As long as the third line remains skewed with the two given lines, the answer is valid.

Example 7

Aside from AB and EH, name two other pairs of skew lines in the cube shown.

Solution

Look for two segments in the cube that do not lie on the same plane and do not intersect.

Other examples of skew lines are: $AC$ and $DH$, $AF$ and $GH$, and $BE$ and $CG$.

There can be more variations as long as the lines meet the definition of skew lines.

Example 8

Identify three pairs of skew lines in the figure shown below.

Solution

Look for three pairs of segments in the figure above that do not lie on the same plane, are not parallel, and do not intersect.

Three possible pairs of skew lines are: $AI$ and $DE$, $FE$ and $IC$, as well as $BC$ and $GF$.

This problem has multiple possible answers. As long as the lines meet the definition of skew lines, the three pairs will be valid.

So you have finished reading the how many skew lines are in a rectangular prism topic article, if you find this article useful, please share it. Thank you very much. See more: how many pairs of skew lines are in a cube, how many parallel lines in a square, how many parallel lines are in a rectangular prism, how many parallel lines in a trapezium, how many parallel lines in a rectangle, how many parallel lines in a triangle, how many parallel lines does a parallelogram have, how many parallel lines does a rhombus have

Top 28 How Many Skew Lines Are In A Rectangular Prism 10143 Good Rating This Answer

What are skew lines in a rectangular prism?

How many skewed lines are in a cube?

Can you have 3 skew lines?

How do you find skew lines?

What is meant by skew lines?

What is skew lines in graph?

Are skew lines in the same plane?

What are skew lines 3d geometry?

How do you find skew lines in 3d?

What is skew lines in graph?

Which are skew lines A and B?

Are skew lines in the same plane?

Can skew lines have a point in common?

geometry – Pairs of skew lines of a cube – Mathematics Stack Exchange

how many skew lines are in a rectangular prism

Skew lines – Explanation & Examples

Skew Lines — from Wolfram MathWorld

Skew Lines – Definition, Meaning, Formula, Examples

Skew lines – Explanation & Examples

Skew Lines | Geometry (Definiton, Examples, & Video) // Tutors.com

Skew lines – Wikipedia

Skew Lines – Definition, Meaning, Formula, Examples

IXL – Identify parallel, intersecting, and skew lines and planes (Geometry practice)

Welcome to CK-12 Foundation | CK-12 Foundation

Skew lines – Explanation & Examples

Skew Lines — from Wolfram MathWorld

Skew lines – Explanation & Examples

Leave a Comment Cancel reply