Top 13 How To Draw Molecular Orbital Diagrams For Polyatomic Molecules 12858 Votes This Answer

You are looking for information, articles, knowledge about the topic nail salons open on sunday near me how to draw molecular orbital diagrams for polyatomic molecules on Google, you do not find the information you need! Here are the best content compiled and compiled by the Chewathai27.com team, along with other related topics such as: how to draw molecular orbital diagrams for polyatomic molecules molecular orbital theory of polyatomic molecules pdf, hf2 molecular orbital diagram, h2o molecule h2o molecular orbital diagram, Molecular orbital diagram, molecular orbital diagram generator, fhf molecular orbital diagram, lif molecular orbital diagram, sf6 molecular orbital diagram

Is molecular orbital theory applicable for polyatomic molecules?

The concept of a molecular orbital is readily extended to provide a description of the electronic structure of a polyatomic molecule. Indeed molecular orbital theory forms the basis for most of the quantitative theoretical investigations of the properties of large molecules.

How do you draw Mo diagrams step by step?

How many atoms are there in polyatomic molecules?

Polyatomic molecules are electrically neutral groups of three or more atoms held together by covalent bonds.

How many σ bonds and π bonds does the CO2 molecule have?

Therefore, CO2 has 2 pi bonds and 2 sigma bonds. A faster way to determine how many pi bonds the molecule has is to know that a double bond is comprised of 1 sigma and 1 pi bond.

Why is CO2 sp hybridized?

Carbon dioxide basically has a sp hybridization type. This type of hybridization occurs as a result of carbon being bound to two other atoms. Bonds can be either two double bonds or one single + one triple bond. We can determine this by closely observing each atom of CO₂.

How many molecular orbitals do you expect the CO2 molecule to have?

The bonding orbitals of CO2 include two sigma molecular orbitals of ag and b1u symmetry and two π molecular orbitals of b2u and b3u symmetry. Each of these bonding molecular orbitals possesses a higher-energy antibonding partner.

How do I calculate bond order?

---

Molecular Orbital Diagram for polyatomic molecules BeH2, H2O, CO2, NH3, SF6

Molecular Orbital Diagram for polyatomic molecules BeH2, H2O, CO2, NH3, SF6

---

5.4: Larger (Polyatomic) Molecules – Chemistry LibreTexts

• Article author: chem.libretexts.org
• Reviews from users: 36748 Ratings
• Top rated: 4.2
• Lowest rated: 1
• Summary of article content: Articles about 5.4: Larger (Polyatomic) Molecules – Chemistry LibreTexts Updating …
• Most searched keywords: Whether you are looking for 5.4: Larger (Polyatomic) Molecules – Chemistry LibreTexts Updating We can extend the method we used for diatomic molecules to draw the molecular orbitals of more complicated, polyatomic molecules (molecules with more than two atoms). To combine several different …
• Table of Contents:

Read More

Molecular Orbitals – Molecular Orbitals for Polyatomic Molecules

• Article author: www.chemistry.mcmaster.ca
• Reviews from users: 13003 Ratings
• Top rated: 4.6
• Lowest rated: 1
• Summary of article content: Articles about Molecular Orbitals – Molecular Orbitals for Polyatomic Molecules Updating …
• Most searched keywords: Whether you are looking for Molecular Orbitals – Molecular Orbitals for Polyatomic Molecules Updating
• Table of Contents:

Read More

Drawing Molecular Orbital Diagrams – YouTube

• Article author: www.youtube.com
• Reviews from users: 12105 Ratings
• Top rated: 4.2
• Lowest rated: 1
• Summary of article content: Articles about Drawing Molecular Orbital Diagrams – YouTube Updating …
• Most searched keywords: Whether you are looking for Drawing Molecular Orbital Diagrams – YouTube Updating video, chia sẻ, điện thoại có máy ảnh, điện thoại quay video, miễn phí, tải lên
• Table of Contents:

Read More

7.3: How to Build Molecular Orbitals – Chemistry LibreTexts

• Article author: chem.libretexts.org
• Reviews from users: 18932 Ratings
• Top rated: 3.1
• Lowest rated: 1
• Summary of article content: Articles about 7.3: How to Build Molecular Orbitals – Chemistry LibreTexts Updating …
• Most searched keywords: Whether you are looking for 7.3: How to Build Molecular Orbitals – Chemistry LibreTexts Updating The molecular orbital (MO) theory is a powerful and extensive approach which describes electrons as delocalized moieties over adjacent atoms. The applications of the MO theory extend beyond the …
• Table of Contents:

Introduction

FUNDAMENTAL STEPS IN DERIVING MO DIAGRAMS

Building Molecular Orbital Diagrams for Homonuclear and Heteronuclear Diatomic Molecules

References

Contributors

Read More

MO Diagram CO2 – YouTube

• Article author: www.youtube.com
• Reviews from users: 2046 Ratings
• Top rated: 4.2
• Lowest rated: 1
• Summary of article content: Articles about MO Diagram CO2 – YouTube Updating …
• Most searched keywords: Whether you are looking for MO Diagram CO2 – YouTube Updating video, chia sẻ, điện thoại có máy ảnh, điện thoại quay video, miễn phí, tải lên
• Table of Contents:

Read More

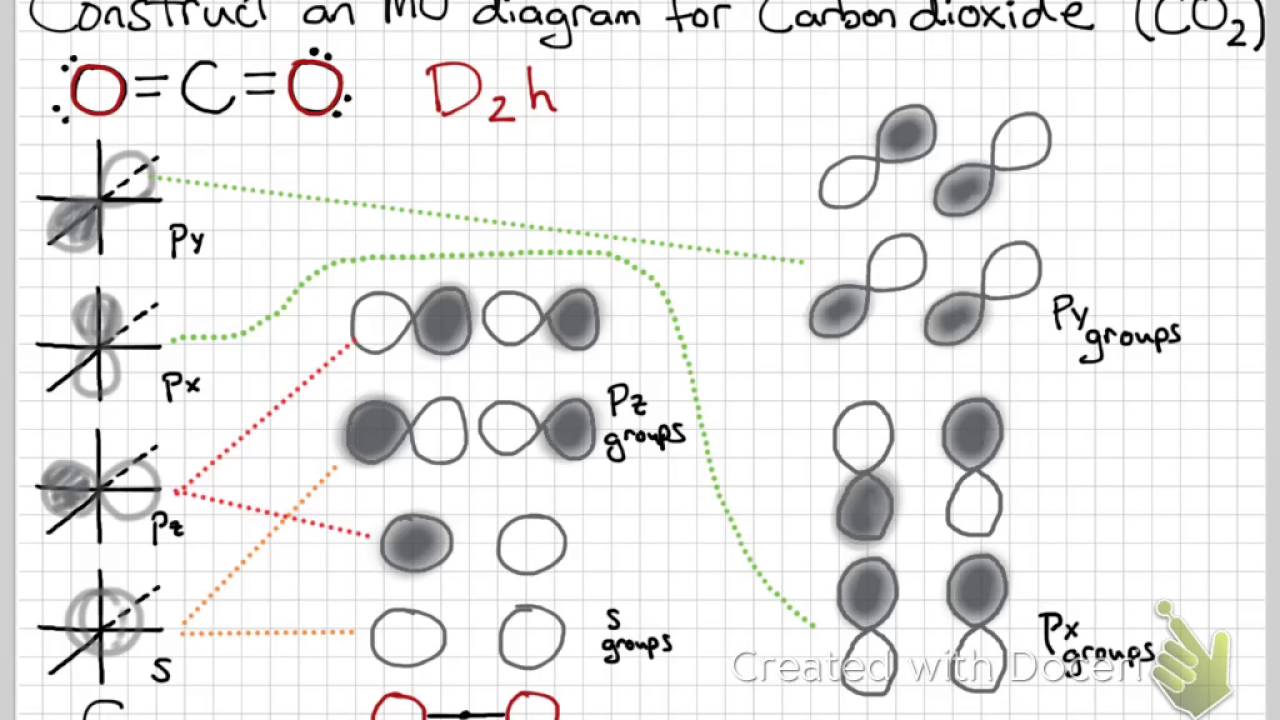
how to draw molecular orbital diagrams for polyatomic molecules

• Article author: www1.lasalle.edu
• Reviews from users: 10209 Ratings
• Top rated: 3.6
• Lowest rated: 1
• Summary of article content: Articles about how to draw molecular orbital diagrams for polyatomic molecules The Walsh diagram shows what happens to the molecular orbitals for a set of molecules which are related in structure. In this case, the difference is the H-X-H. …
• Most searched keywords: Whether you are looking for how to draw molecular orbital diagrams for polyatomic molecules The Walsh diagram shows what happens to the molecular orbitals for a set of molecules which are related in structure. In this case, the difference is the H-X-H.
• Table of Contents:

Read More

Molecular Orbitals – Molecular Orbitals for Polyatomic Molecules

• Article author: www.chemistry.mcmaster.ca
• Reviews from users: 22527 Ratings
• Top rated: 3.4
• Lowest rated: 1
• Summary of article content: Articles about Molecular Orbitals – Molecular Orbitals for Polyatomic Molecules Updating …
• Most searched keywords: Whether you are looking for Molecular Orbitals – Molecular Orbitals for Polyatomic Molecules Updating
• Table of Contents:

Read More

MO Diagram – Overview, How to draw MO Diagram and Solved example along with FAQs

• Article author: byjus.com
• Reviews from users: 42852 Ratings
• Top rated: 3.7
• Lowest rated: 1
• Summary of article content: Articles about MO Diagram – Overview, How to draw MO Diagram and Solved example along with FAQs Updating …
• Most searched keywords: Whether you are looking for MO Diagram – Overview, How to draw MO Diagram and Solved example along with FAQs Updating MO Diagram – A molecular orbital diagram, also known as a MO diagram, is a qualitative descriptive tool used to explain chemical bonding in molecules using molecular orbital theory in general and the linear combination of atomic orbitals (LCAO) method in particular. As atoms bond to form molecules, a certain number of atomic orbitals combine to form the same number of molecular orbitals, though the electrons involved may be redistributed among the orbitals.
• Table of Contents:

Table of Contents

Overview of MO Diagram

How to Draw MO Diagram

Relationship Between Electronic Configuration and Molecular Behaviour

Solved Example

Frequently Asked Questions on MO Diagram

Read More

Molecular orbital theory for polyatomic molecules? | Socratic

• Article author: socratic.org
• Reviews from users: 7038 Ratings
• Top rated: 4.5
• Lowest rated: 1
• Summary of article content: Articles about Molecular orbital theory for polyatomic molecules? | Socratic Updating …
• Most searched keywords: Whether you are looking for Molecular orbital theory for polyatomic molecules? | Socratic Updating There kind of is, but it builds off of molecular orbital theory and is very difficult to articulate in an accessible way. The core premises of this method are: In a molecule with more than two atoms, any orbitals with directional aspects (i.e. not spheres) pointing towards the central atom are considered to be along the \mathbf(y) axis (rather than the z axis). Each atom surrounding a central atom is considered to have its own set of axes. So, each atom has different x and z axes. The orbitals of the surrounding atoms are considered to “transform” as “group orbitals”, meaning that they bond to the atoms of the central atom as a group. As usual, only compatible orbitals can overlap with each other (just like in MO theory). As a brief overview of the idea of individual axes, consider this image of a tetrahedral set of axes: This gets complicated very quickly, so I’ll simply work with “NH”_3, a relatively simple but not overly simple case (ask if you need help). Recall that this is a trigonal pyramidal molecule. We will be using a method called Symmetry-Adapted Linear Combinations (SALCs). What that means is that we’ll determine how to categorize certain orbitals to determine which ones are allowed to overlap. Then, we’ll build the MO diagram from scratch. The overall steps we’ll be following are: Finding the point group. Finding the reducible representation based on how the hydrogen atoms behave. Reducing the reducible representation to its irreducible representations. Assigning those to the group of hydrogens. Determining which orbitals are compatible. Making the MO diagram. SYMMETRY CONSIDERATIONS Ammonia belongs to what is called the C_(3v) “point group”, because it has a principal, C_3 rotation axis, and because it has a vertical mirror plane sigma_v. A hatC_3 operation is when you rotate 360^@/3 = 120^@ and achieve the original molecule back. It is the C_3 symmetry element that acts as the \mathbf(z) axis of “NH”_3. This is a common convention. A hatsigma_v operation is when you reflect through a mirror plane that is vertically aligned. A sigma_v mirror plane is colinear with the z axis (if it was perpendicular it would be a sigma_h). DETERMINING THE REDUCIBLE REPRESENTATION The irreducible representations, or IRREPs, are what we will use to categorize the ways the hydrogens “behave” around the nitrogen. Given that “NH”_3 belongs to the C_(3v) point group, it is associated with what’s called a character table: To determine the irreducible representations, we first need the reducible representations, Gamma (gamma), for the hydrogens as a group. To do that, we follow these steps: For each symmetry element (E, the identity, C_3(z), the principal rotation, and sigma_v, the vertical mirror plane), operate on the hydrogen atoms as a group and see where each one ends up. The hydrogens that stay where they are and do NOT move contribute 1 to Gamma. The hydrogens that DO move contribute 0 to Gamma. The hydrogens that change orbital sign contribute -1 to Gamma. Now, let’s align the molecule in a more convenient way. Let the z axis be pointing towards you. Thus, as we said before, the C_3 axis IS the z axis. We see that there are three sigma_v mirror planes (a,b,c) and three hydrogens (H_a, H_b, H_c). Now, let’s see what happens if we perform each symmetry operation. hatE: color(green)(H_a -> H_a) color(green)(H_b -> H_b) color(green)(H_c -> H_c) Thus, we get 1 + 1 + 1 = color(blue)(3) for the first number in Gamma for the E operation (the identity operation). hatC_3(z) (counterclockwise): H_a -> H_b H_b -> H_c H_c -> H_a Each hydrogen moved, and none of them stayed where they are, so this operation contributes color(blue)(0) to Gamma. hatsigma_v: color(green)(H_a -> H_a) H_b harr H_c H_a stayed in place, but H_b and H_c swapped places. So, there is a contribution of color(blue)(1) to Gamma. Since ammonia is symmetrical and each hydrogen is identical, performing hatsigma_v(a), hatsigma_v(b), and hatsigma_v(c) each do the same thing, so we do not need to do all three. The reducible representation then, using the 1s atomic orbitals of hydrogen as a basis, is written as: color(blue)(” “” “” “E” “C_3(z)” “sigma_v) color(blue)(Gamma_(1s) = ” 3″” “0” “” “” “1) Phew, now let’s reduce this! THE IRREDUCIBLE REPRESENTATIONS Basically, the rows in the character table above have to add up to give Gamma. The result becomes: So, the group orbitals of hydrogen “transform under A_1 and E symmetry”. What does THAT mean? It means that they can either symmetrically behave one at a time (A_1), or two at a time (E). This is depicted as follows: In this one, the hydrogen 1s orbitals are all the same sign, and no matter what happens, they stay the same sign. In this one, there is one hydrogen 1s orbital that is the opposite sign to the others, and a horizontal node exists. This one is similar to E(y), but the node is perpendicular to the horizontal node in E(x) (the third hydrogen doesn’t matter here). FINALLY DRAWING THE MO DIAGRAM! Okay, finally, we have enough information to draw an approximate MO diagram. To save time (and brain), I’m just going to have to tell you the symmetries of nitrogen’s orbitals. The 2s is A_1, the 2p_z is A_1, and the 2p_y and 2p_x are collectively E. The orbitals will combine like so: “3H” A_1 with “N” A_1 (bonding, antibonding) “3H” E(x) with “N” E (bonding, antibonding) “3H” E(y) with “N” E (bonding, antibonding)) “Nothing” with “N” A_1 (nonbonding) Using the orbital potential energies (Appendix B.9) of each atom, we eventually get: Note that we came in with seven orbitals (3xxH + “N”_(2s) + “N”_(2p_x) + “N”_(2p_y) + “N”_(2pz)) and came out with seven (2a_1, 3a_1, 4a_1, 2xx1e, 2xx2e). Also note that only the orbitals of the same symmetry (A_1 with A_1, E with E, etc.) can interact with each other—in other words, they are compatible. You can trace that by looking at the dashed lines. The first three bonding MOs of “NH”_3 account for the three single bonds, and the highest-energy MO holds the lone pair of electrons on nitrogen (it is fairly nonbonding). And here is a reference (Inorganic Chemistry, Miessler et al., pg. 156) to show the actual MO diagram.
• Table of Contents:

Read More

Molecular orbital theory for polyatomic molecules? | Socratic

• Article author: medium.com
• Reviews from users: 6628 Ratings
• Top rated: 4.2
• Lowest rated: 1
• Summary of article content: Articles about Molecular orbital theory for polyatomic molecules? | Socratic Updating …
• Most searched keywords: Whether you are looking for Molecular orbital theory for polyatomic molecules? | Socratic Updating There kind of is, but it builds off of molecular orbital theory and is very difficult to articulate in an accessible way. The core premises of this method are: In a molecule with more than two atoms, any orbitals with directional aspects (i.e. not spheres) pointing towards the central atom are considered to be along the \mathbf(y) axis (rather than the z axis). Each atom surrounding a central atom is considered to have its own set of axes. So, each atom has different x and z axes. The orbitals of the surrounding atoms are considered to “transform” as “group orbitals”, meaning that they bond to the atoms of the central atom as a group. As usual, only compatible orbitals can overlap with each other (just like in MO theory). As a brief overview of the idea of individual axes, consider this image of a tetrahedral set of axes: This gets complicated very quickly, so I’ll simply work with “NH”_3, a relatively simple but not overly simple case (ask if you need help). Recall that this is a trigonal pyramidal molecule. We will be using a method called Symmetry-Adapted Linear Combinations (SALCs). What that means is that we’ll determine how to categorize certain orbitals to determine which ones are allowed to overlap. Then, we’ll build the MO diagram from scratch. The overall steps we’ll be following are: Finding the point group. Finding the reducible representation based on how the hydrogen atoms behave. Reducing the reducible representation to its irreducible representations. Assigning those to the group of hydrogens. Determining which orbitals are compatible. Making the MO diagram. SYMMETRY CONSIDERATIONS Ammonia belongs to what is called the C_(3v) “point group”, because it has a principal, C_3 rotation axis, and because it has a vertical mirror plane sigma_v. A hatC_3 operation is when you rotate 360^@/3 = 120^@ and achieve the original molecule back. It is the C_3 symmetry element that acts as the \mathbf(z) axis of “NH”_3. This is a common convention. A hatsigma_v operation is when you reflect through a mirror plane that is vertically aligned. A sigma_v mirror plane is colinear with the z axis (if it was perpendicular it would be a sigma_h). DETERMINING THE REDUCIBLE REPRESENTATION The irreducible representations, or IRREPs, are what we will use to categorize the ways the hydrogens “behave” around the nitrogen. Given that “NH”_3 belongs to the C_(3v) point group, it is associated with what’s called a character table: To determine the irreducible representations, we first need the reducible representations, Gamma (gamma), for the hydrogens as a group. To do that, we follow these steps: For each symmetry element (E, the identity, C_3(z), the principal rotation, and sigma_v, the vertical mirror plane), operate on the hydrogen atoms as a group and see where each one ends up. The hydrogens that stay where they are and do NOT move contribute 1 to Gamma. The hydrogens that DO move contribute 0 to Gamma. The hydrogens that change orbital sign contribute -1 to Gamma. Now, let’s align the molecule in a more convenient way. Let the z axis be pointing towards you. Thus, as we said before, the C_3 axis IS the z axis. We see that there are three sigma_v mirror planes (a,b,c) and three hydrogens (H_a, H_b, H_c). Now, let’s see what happens if we perform each symmetry operation. hatE: color(green)(H_a -> H_a) color(green)(H_b -> H_b) color(green)(H_c -> H_c) Thus, we get 1 + 1 + 1 = color(blue)(3) for the first number in Gamma for the E operation (the identity operation). hatC_3(z) (counterclockwise): H_a -> H_b H_b -> H_c H_c -> H_a Each hydrogen moved, and none of them stayed where they are, so this operation contributes color(blue)(0) to Gamma. hatsigma_v: color(green)(H_a -> H_a) H_b harr H_c H_a stayed in place, but H_b and H_c swapped places. So, there is a contribution of color(blue)(1) to Gamma. Since ammonia is symmetrical and each hydrogen is identical, performing hatsigma_v(a), hatsigma_v(b), and hatsigma_v(c) each do the same thing, so we do not need to do all three. The reducible representation then, using the 1s atomic orbitals of hydrogen as a basis, is written as: color(blue)(” “” “” “E” “C_3(z)” “sigma_v) color(blue)(Gamma_(1s) = ” 3″” “0” “” “” “1) Phew, now let’s reduce this! THE IRREDUCIBLE REPRESENTATIONS Basically, the rows in the character table above have to add up to give Gamma. The result becomes: So, the group orbitals of hydrogen “transform under A_1 and E symmetry”. What does THAT mean? It means that they can either symmetrically behave one at a time (A_1), or two at a time (E). This is depicted as follows: In this one, the hydrogen 1s orbitals are all the same sign, and no matter what happens, they stay the same sign. In this one, there is one hydrogen 1s orbital that is the opposite sign to the others, and a horizontal node exists. This one is similar to E(y), but the node is perpendicular to the horizontal node in E(x) (the third hydrogen doesn’t matter here). FINALLY DRAWING THE MO DIAGRAM! Okay, finally, we have enough information to draw an approximate MO diagram. To save time (and brain), I’m just going to have to tell you the symmetries of nitrogen’s orbitals. The 2s is A_1, the 2p_z is A_1, and the 2p_y and 2p_x are collectively E. The orbitals will combine like so: “3H” A_1 with “N” A_1 (bonding, antibonding) “3H” E(x) with “N” E (bonding, antibonding) “3H” E(y) with “N” E (bonding, antibonding)) “Nothing” with “N” A_1 (nonbonding) Using the orbital potential energies (Appendix B.9) of each atom, we eventually get: Note that we came in with seven orbitals (3xxH + “N”_(2s) + “N”_(2p_x) + “N”_(2p_y) + “N”_(2pz)) and came out with seven (2a_1, 3a_1, 4a_1, 2xx1e, 2xx2e). Also note that only the orbitals of the same symmetry (A_1 with A_1, E with E, etc.) can interact with each other—in other words, they are compatible. You can trace that by looking at the dashed lines. The first three bonding MOs of “NH”_3 account for the three single bonds, and the highest-energy MO holds the lone pair of electrons on nitrogen (it is fairly nonbonding). And here is a reference (Inorganic Chemistry, Miessler et al., pg. 156) to show the actual MO diagram.
• Table of Contents:

Read More

how to draw molecular orbital diagrams for polyatomic molecules

• Article author: authors.library.caltech.edu
• Reviews from users: 18163 Ratings
• Top rated: 3.1
• Lowest rated: 1
• Summary of article content: Articles about how to draw molecular orbital diagrams for polyatomic molecules The molecular-orbital method that we applied to diatomic molecules proves … general method for constructing molecular wave functions for polyatomic. …
• Most searched keywords: Whether you are looking for how to draw molecular orbital diagrams for polyatomic molecules The molecular-orbital method that we applied to diatomic molecules proves … general method for constructing molecular wave functions for polyatomic.
• Table of Contents:

Read More

Lecture 28: Molecular Orbital Theory for Polyatomic Molecules | Principles of Chemical Science | Chemistry | MIT OpenCourseWare

• Article author: ocw.mit.edu
• Reviews from users: 1988 Ratings
• Top rated: 4.3
• Lowest rated: 1
• Summary of article content: Articles about Lecture 28: Molecular Orbital Theory for Polyatomic Molecules | Principles of Chemical Science | Chemistry | MIT OpenCourseWare MIT OpenCourseWare is a web based publication of virtually all MIT course content. OCW is open and available to the world and is a permanent MIT activity. …
• Most searched keywords: Whether you are looking for Lecture 28: Molecular Orbital Theory for Polyatomic Molecules | Principles of Chemical Science | Chemistry | MIT OpenCourseWare MIT OpenCourseWare is a web based publication of virtually all MIT course content. OCW is open and available to the world and is a permanent MIT activity. MIT OpenCourseWare is a web based publication of virtually all MIT course content. OCW is open and available to the world and is a permanent MIT activityopencourseware,MIT OCW,courseware,MIT opencourseware,Free Courses,class notes,class syllabus,class materials,tutorials,online courses,MIT courses
• Table of Contents:

Read More

---

See more articles in the same category here: https://chewathai27.com/toplist.

5.4: Larger (Polyatomic) Molecules

Symmetry adapted linear combinations (SALCs)

We need SALCs (aka group orbitals) to draw molecular orbital (MO) diagrams of polyatomic molecules. SALCs are groups of orbitals on pendant atoms. These groups of orbitals much match the symmetry of valence orbitals on the central atom in order to create a productive interaction. When we combine SALCs with the atomic orbitals on the central atom, we can generate a MO diagram that gives us information about the molecule’s bonding and electronic states.

Below is a set of steps you can follow to find SALCs and draw a MO Diagram. Each step will be illustrated in detail through the examples in the subsections that follow this page.

Find the point group of the molecule and assign Cartesian coordinates so that \(z\) is the principle axis.

Sometimes we can simplify things by only looking only at the point group of the relevant orbitals.* Only simplify when instructed to do so. Identify and count the pendant atoms’ valence orbitals.

Is there more than 1 type for each atom (ex. just s, or s and p?) We expect 1 SALC for each ligand orbital. Generate a reducible representation (\(\Gamma\)) for the group of pendant atom orbitals using the appropriate character table.

You have to do this for each set of orbital types. If you only have s orbitals for each ligand, you only need to generate 1 reducible representation. If you have \(p\) orbitals, you would generate additional \(\Gamma\)’s for \(p_x\), \(p_y\), and \(p_z\). Break the \(\Gamma\) into its component irreducible representations from the character table. Note the symmetry of each irreducible representation, its associated orbitals, and their degeneracy. If you are asked to sketch the shapes of SALCs, determine what they “look like” using one of the following strategies.

(a) Shortcut: if the reducible representations are listed with s, p, or d orbitals in the character table, just draw them (…and skip steps b-c)

(b) Systematic method: Draw an expanded character table and draw your molecule with each ligand identified by letters or numbers (a,b,c… or i,j,k… or 1,2,3…) Determine where each pendant atom/orbital ends up under each of the operations of your expanded table. Project the values for each irreducible representation onto the chart you created and then add up the values. Positive and negative values are opposite signed orbitals. Draw the MO diagram by combining SALCs with AO’s of like symmetry. When drawing SALC energy levels, remember that the more nodal planes in your SALC orbital drawings, the higher the energy or that SALC orbital.

* When we are focused on orbitals, as in the case for finding group orbitals and drawing molecular orbital diagrams, the symmetry of the orbitals are what we are interested in. In the case of high-symmetry point groups, like \(D_{\infty h}\) and \(C_{\infty v}\) even though the molecule may have a \(C_\infty\) axis, the orbitals do not necessarily retain this symmetry element. For example, the \(p_x\) orbital would not have a \(C_\infty\) axix, but rather a \(C_2\) axis. It is sufficient and useful to substitute \(D_{2h}\) for \(D_{\infty h}\) and \(C_{2v}\) for \(C_{\infty v}\) to simplify the problem.

Molecular Orbitals for Polyatomic Molecules

Molecular Orbitals for Polyatomic Molecules

The concept of a molecular orbital is readily extended to provide a description of the electronic structure of a polyatomic molecule. Indeed molecular orbital theory forms the basis for most of the quantitative theoretical investigations of the properties of large molecules.

In general a molecular orbital in a polyatomic system extends over all the nuclei in a molecule and it is essential, if we are to understand and predict the spatial properties of the orbitals, that we make use of the symmetry properties possessed by the nuclear framework. An analysis of the molecular orbitals for the water molecule provides a good introduction to the way in which the symmetry of a molecule determines the forms of the molecular orbitals in a polyatomic system.

There are three symmetry operations which transform the nuclear framework of the water molecule into itself and hence leave the nuclear potential field in which the electrons move unchanged (Fig. 8-10).

Fig. 8-10. Symmetry elements for H 2 O. The bottom two diagrams illustrate the transformations of the 2p y orbital on oxygen under the C 2 and s 2 symmetry operations.

For each symmetry operation there is a corresponding symmetry element. The symmetry elements for the water molecule are a two-fold axis of rotation C 2 and two planes of symmetry s 1 and s 2 (Fig. 8-10). A rotation of 180° about the C 2 axis leaves the oxygen nucleus unchanged and interchanges the two hydrogen nuclei. A reflection through the plane labelled s 1 leaves all the nuclear positions unchanged while a reflection through s 2 interchanges the two protons. The symmetry operations associated with the three symmetry elements either leave the nuclear positions unchanged or interchange symmetrically equivalent (and hence indistinguishable) nuclei. Every molecular orbital for the water molecule must, under the same symmetry operations, be left unchanged or undergo a change in sign.

Similarly we may use the symmetry transformation properties of the atomic orbitals on oxygen and hydrogen together with their relative orbital energy values to determine the primary atomic components of each molecular orbital in a simple LCAO approximation to the exact molecular orbitals. Only atomic orbitals which transform in the same way under the symmetry operations may be combined to form a molecular orbital of a given symmetry. The symmetry transformation properties of the atomic orbitals on oxygen and hydrogen are given in Table 8-3. A value of +1 or -1 opposite a given orbital in the table indicates that the orbital is unchanged or changed in sign respectively by a particular symmetry operation.

Table 8-3.

Symmetry Properties and Orbital Energies for the Water Molecule

Atomic Orbitals

on Oxygen Symmetry Behaviour Under Symmetry

Classification Orbital Energy (au) s 2 s 1 s 2 1s +1 +1 +1 a 1 -20.669 2s +1 +1 +1 a 1 -1.244 2p z +1 +1 +1 a 1 } -0.632 2p x -1 +1 -1 b 2 2p y -1 -1 +1 b 1 Atomic Orbitals on Hydrogen (1s 1 + 1s 2 ) +1 +1 +1 a 1 } -0.500 (1s 1 – 1s 2 ) -1 +1 -1 b 2

Molecular Orbital Energies for H 2 O (au) 1a 1 2a 1 1b 2 3a 1 1b 1 -20.565 -1.339 -0.728 -0.595 -0.521

The 1s, 2s and 2p z orbitals of oxygen are symmetric (i.e., unchanged) with respect to all three symmetry operations. They are given the symmetry classification a 1 . The 2p x orbital, since it possesses a node in the s 2 plane (and hence is of different sign on each side of the plane) changes sign when reflected through the s 2 plane or when rotated by 180° about the C 2 axis. It is classified as a b 2 orbital. The 2p y orbital is antisymmetric with respect to the rotation operator and to a reflection through the s 1 plane. It is labelled b 1 .

The hydrogen 1s orbitals when considered separately are neither unchanged nor changed in sign by the rotation operator or by a reflection through the s 2 plane. Instead both these operations interchange these orbitals. The hydrogen orbitals are said to be symmetrically equivalent and when considered individually they do not reflect the symmetry properties of the molecule. However, the two linear combinations (1s 1 + 1s 2 ) and (1s 1 – 1s 2 ) do behave in the required manner. The former is symmetric

under all three operations and is of a 1 symmetry while the latter is antisymmetric with respect to the rotation operator and to a reflection through the plane s 2 and is of b 2 symmetry.

The molecular orbitals in the water molecule are classified as a 1 , b 1 or b 2 orbitals, as determined by their symmetry properties. This labelling of the orbitals is analogous to the use of the s-p and g-u classification in linear molecules. In addition to the symmetry properties of the atomic orbitals we must consider their relative energies to determine which orbitals will overlap significantly and form delocalized molecular orbitals.

The 1s atomic orbital on oxygen possesses a much lower energy than any of the other orbitals of a 1 symmetry and should not interact significantly with them. The molecular orbital of lowest energy in H 2 O should therefore correspond to an inner shell 1s atomic-like orbital centred on the oxygen. This is the first orbital of a 1 symmetry and it is labelled la 1 . Reference to the forms of the charge density contours for the la, molecular orbital (Fig. 8-11) substantiates the above remarks regarding the properties of this orbital.

Fig. 8-11. Contour maps of the molecular orbital charge densities for H 2 O. The maps for the la 1 , 2a 1 , 3a 1 and 1b 2 orbitals (all doubly-occupied) are shown in the plane of the nuclei. The lb 1 orbital has a node in this plane and hence the contour map for the 1b 1 orbital is shown in the plane perpendicular to the molecular plane. The total molecular charge density for H 2 O is also illustrated. The density distributions were calculated from the wave function determined by R. M. Pitzer, S. Aung and S. I. Chan, J. Chem. Phys. 49, 2071 (1968). Click here for contour values.

Notice that the orbital energy of the la 1 molecular orbital is very similar to that for the 1s atomic orbital on oxygen. The 1a 1 orbital in H 2 O is, therefore, similar to the l s inner shell molecular orbitals of the diatomic hydrides.

The atomic orbital of next lowest energy in this system is the 2s orbital of a 1 symmetry on oxygen. We might anticipate that the extent to which this orbital will overlap with the (1s 1 + 1s 2 ) combination of orbitals on the hydrogen atoms to form the 2a 1 molecular orbital will be intermediate between that found for the 2 s molecular orbitals in the diatomic hydrides CH and HF (Fig. 8-9). The 2 s orbital in CH results from a strong mixing of the 2s orbital on carbon and the hydrogen 1s orbital. In HF the participation of the hydrogen orbital in the 2 s orbital is greatly reduced, a result of the lower energy of the 2s atomic orbital on fluorine as compared to that of the 2s orbital on carbon.

Aside from the presence of the second proton, the general form and nodal structure of the 2a 1 density distribution in the water molecule is remarkably similar to the 2 s distributions in CH and HF, and particularly to the latter. The charge density accumulated on the bonded side of the oxygen nucleus in the 2a 1 orbital is localized near this nucleus as the corresponding charge increase in the 2 s orbital of HF is localized near the fluorine. The charge density of the 2a 1 molecular orbital accumulated in the region between the three nuclei will exert a force drawing all three nuclei together. The 2a 1 orbital is a binding orbital.

Although the three 2p atomic orbitals are degenerate in the oxygen atom the presence of the two protons results in each 2p orbital experiencing a different potential field in the water molecule. The nonequivalence of the 2p orbitals in the water molecule is evidenced by all three possessing different symmetry properties. The three 2p orbitals will interact to different extents with the protons and their energies will differ.

The 2p x orbital interacts most strongly with the protons and forms an orbital of b 2 symmetry by overlapping with the (1s 1 – 1s 2 ) combination of 1s orbitals on the hydrogens. The charge density contours for the lb 2 orbital indicate that this simple LCAO description accounts for the principal features of this molecular orbital. The lb 2 orbital concentrates charge density along each O-H bond axis and draws the nuclei together. The charge density of the 1b 2 orbital binds all three nuclei. In terms of the forces exerted on the nuclei the 2a 1 and lb 2 molecular orbitals are about equally effective in binding the protons in the water molecule.

The 2p z orbital may also overlap with the hydrogen 1s orbitals, the (1s 1 + 1s 2 ) a 1 combination, and the result is the 3a 1 molecular orbital. This orbital is concentrated along the z-axis and charge density is accumulated in both the bonded and nonbonded sides of the oxygen nucleus. It exerts a binding force on the protons and an antibinding force on the oxygen nucleus, a behaviour similar to that noted before for the 3 s orbitals in CH and HF.

The 2p y orbital is not of the correct symmetry to overlap with the hydrogen 1s orbitals. To a first approximation the 1b 1 molecular orbital will be simply a 2p y atomic orbital on the oxygen, perpendicular to the plane of the molecule. Reference to Fig. 8-11 indicates that the 1b 1 orbital does resemble a 2p atomic orbital on oxygen but one which is polarized into the molecule by the field of the protons. The 1b 1 molecular orbital of H 2 O thus resembles a single component of the 1 p molecular orbitals of the diatomic hydrides. The 1b 1 and the 1 p orbitals are essentially nonbinding. They exert a small binding force on the heavy nuclei because of the slight polarization. The force exerted on the protons by the pair of electrons in the 1b 1 orbital is slightly less than that required to balance the force of repulsion exerted by two of the nuclear charges on the oxygen nucleus. The 1b 1 and 1 p electrons basically do no more than partially screen nuclear charge on the heavy nuclei from the protons.

In summary, the electronic configuration of the water molecule as determined by molecular orbital theory is

1a 2 1 2a 2 1 1b 2 2 3a 2 1 1b 2 1

1

1

1

2

1

1

y

Before closing this introductory account of molecular orbital theory, brief mention should be made of the very particular success which the application of this theory has had in the understanding of the chemistry of a class of organic molecules called conjugated systems. Conjugated molecules are planar organic molecules consisting of a framework of carbon atoms joined in chains or rings by alternating single and double bonds. Some examples are

In the structural formulae for the cyclic molecules, e.g., benzene and naphthalene, it is usual not to label the positions of the carbon and hydrogen atoms by their symbols. A carbon atom joined to just two other carbon atoms is in addition bonded to a hydrogen atom, the C�H bond axis being projected out of the ring in the plane of the carbon framework and bisecting

the CCC bond angle.

The notion of these molecules possessing alternating single and double bonds is a result of our attempt to describe the bonding in terms of conventional chemical structures. In reality all six C�C bonds in benzene are identical and the C�C bonds in the other two examples possess properties intermediate between those for single and double bonds. In other words, the pairs of electrons forming the second or p bonds are not localized between specific carbon atoms but are delocalized over the whole network of carbon atoms, a situation ideally suited for a molecular orbital description.

7.3: How to Build Molecular Orbitals

The molecular orbital (MO) theory is a powerful and extensive approach which describes electrons as delocalized moieties over adjacent atoms. The applications of the MO theory extend beyond the limitations of the Valence Shell Electron Pair Repulsion (VSEPR) model and the Valence Bond theory. These previous theories provide substantial information on predicting the structure and bonding properties of a molecule by portraying electrons as localized “balloons” of high density.

Introduction

Although VSEPR and the Valence Bond theory accurately predict bond properties, they fail to fully explain some molecules. The MO theory incorporates the wave character of electrons in developing MO diagrams. MO diagrams predict physical and chemical properties of a molecule such as shape, bond energy, bond length and bond angle. They also provide information in predicting a molecule’s electronic spectra and paramagnetism. The objective of this wiki is to provide readers with the fundamental steps in constructing simple homonuclear and heteronuclear diatomic molecular orbital diagrams. These steps may then be extrapolated to construct more difficult polyatomic diagrams.

Molecular Orbitals

The region an electron is most likely to be found in a molecule. A MO is defined as the combination of atomic orbitals.

Homonuclear Diatomics

Molecules consisting of two identical atoms are said to be homonuclear diatomic, such as: H 2 , N 2 , O 2 , and F 2 .

Heteronuclear Diatomics

Molecules consisting of two non-identical atoms are said to be heteronuclear diatomic, such as: CO, NO, HF, and LiF.

Bonding and Antibonding Orbitals

Orbitals that are out-of-phase with one of another are “antibonding” orbitals because regions with dense electron probabilities do not merge which destabilizes the molecule. “Bonding” orbitals are less energetic than antibonding atomic orbitals and are in-phase, as depicted in the figure below. Note how the bonding orbitals come together constructively, while the antibonding orbitals do not.

Phases and nodes

Phases are designated either (+) or (-) relative to their wave “up” or wave “down” displacements. A node occurs if the phase signs change from (+) to (-) or vice versa. It is important to notice that the phase signs do NOT symbolize charges. Nodes are regions where the probability of finding an electron is ZERO.

Sigma and Pi Bonds

A sigma-bond is an “end-to-end” bond formed from symmetric atomic orbitals. A pi-bond is formed from a “sideways” overlap.

General Notes on Molecular Orbital Diagrams

So you have finished reading the how to draw molecular orbital diagrams for polyatomic molecules topic article, if you find this article useful, please share it. Thank you very much. See more: molecular orbital theory of polyatomic molecules pdf, hf2 molecular orbital diagram, h2o molecule h2o molecular orbital diagram, Molecular orbital diagram, molecular orbital diagram generator, fhf molecular orbital diagram, lif molecular orbital diagram, sf6 molecular orbital diagram