Top 46 2 차 저역 통과 필터 Top Answer Update

You are looking for information, articles, knowledge about the topic nail salons open on sunday near me 2 차 저역 통과 필터 on Google, you do not find the information you need! Here are the best content compiled and compiled by the https://chewathai27.com/to team, along with other related topics such as: 2 차 저역 통과 필터 2차 저역통과필터 해석, 1차 2차 저역통과필터, 2차 저역통과필터 전압이득, 3차 저역 통과 필터, 2차 저역통과필터 차단주파수, 2차 필터, 2차 저역통과필터 전달함수, 2차 수동 필터

Operational Amplifiers . Primary and Secondary Low Pass Filters ( LPF)

Sallen-key 2차 저역 통과 필터 (셀런키 필터) : 네이버 블로그

Article author: m.blog.naver.com
Reviews from users: 30355 Ratings
Top rated: 3.2
Lowest rated: 1
Summary of article content: Articles about Sallen-key 2차 저역 통과 필터 (셀런키 필터) : 네이버 블로그 2차 Low pass filter 구조 입니다. 차수는 C의 갯수로 판단해주시면 되고요~! 차단 주파수는 fc = 1/(2*pi*R*C)로 정의가 됩니다. …
Most searched keywords: Whether you are looking for Sallen-key 2차 저역 통과 필터 (셀런키 필터) : 네이버 블로그 2차 Low pass filter 구조 입니다. 차수는 C의 갯수로 판단해주시면 되고요~! 차단 주파수는 fc = 1/(2*pi*R*C)로 정의가 됩니다.
Table of Contents:

카테고리 이동

스탠드님의블로그

이 블로그
아날로그 회로
카테고리 글

카테고리

이 블로그
아날로그 회로
카테고리 글

Sallen-key 2차 저역 통과 필터 (셀런키 필터) : 네이버 블로그

Article author: contents.kocw.or.kr
Reviews from users: 29017 Ratings
Top rated: 4.7
Lowest rated: 1
Summary of article content: Articles about 2 차 저역 통과 필터 저역통과 필터 응답 (low-pass filter (LPF) response) … 고역통과 필터 응답 (high-pass filter (HPF) response) … 예제: 2차 버터워스 (Butterworth) 응답. …
Most searched keywords: Whether you are looking for 2 차 저역 통과 필터 저역통과 필터 응답 (low-pass filter (LPF) response) … 고역통과 필터 응답 (high-pass filter (HPF) response) … 예제: 2차 버터워스 (Butterworth) 응답.
Table of Contents:

2 차 저역 통과 필터

Article author: cms3.koreatech.ac.kr
Reviews from users: 43836 Ratings
Top rated: 3.1
Lowest rated: 1
Summary of article content: Articles about 2 차 저역 통과 필터 2차 LPF (Second order Low Pass Filter). • 고차필터(Higher order filters). • 다중궤환 대역통과필터(MFB bandpass filters). • 대역저지필터(Bandstop filters). …
Most searched keywords: Whether you are looking for 2 차 저역 통과 필터 2차 LPF (Second order Low Pass Filter). • 고차필터(Higher order filters). • 다중궤환 대역통과필터(MFB bandpass filters). • 대역저지필터(Bandstop filters).
Table of Contents:

2 차 저역 통과 필터

Article author: newgh.gnu.ac.kr
Reviews from users: 33244 Ratings
Top rated: 3.5
Lowest rated: 1
Summary of article content: Articles about 2 차 저역 통과 필터 차단주파수와 전압이득은 다음과 같이 표현된다. 및. (1) 회로도 그리기. ① 1차 고역통과필터회로를 회로도면 상에 그린다. (2) … …
Most searched keywords: Whether you are looking for 2 차 저역 통과 필터 차단주파수와 전압이득은 다음과 같이 표현된다. 및. (1) 회로도 그리기. ① 1차 고역통과필터회로를 회로도면 상에 그린다. (2) …
Table of Contents:

2 차 저역 통과 필터

Article author: ael.cbnu.ac.kr
Reviews from users: 49948 Ratings
Top rated: 3.3
Lowest rated: 1
Summary of article content: Articles about 2 차 저역 통과 필터 이론부에서 설계한 대역통과 능동필터의 주파수 특성을 … 2. 설계. ㅇ 연산증폭기 이득(전달함수). 그림: 연산 증폭기. ㅇ 저역통과 필터(LPF):. …
Most searched keywords: Whether you are looking for 2 차 저역 통과 필터 이론부에서 설계한 대역통과 능동필터의 주파수 특성을 … 2. 설계. ㅇ 연산증폭기 이득(전달함수). 그림: 연산 증폭기. ㅇ 저역통과 필터(LPF):.
Table of Contents:

2 차 저역 통과 필터

Article author: hu.taphoamini.com
Reviews from users: 38272 Ratings
Top rated: 4.5
Lowest rated: 1
Summary of article content: Articles about 2차 저역통과필터 | [전기전자 강의] 연산 증폭기 30. 1차, 2차 저역통과필터( 로우패스필터. Lpf ), 고역통과필터( 하이패스필터. Hpf) 판별및 차단 주파수 암기법 346 개의 새로운 답변이 업데이트되었습니다. – Hu.taphoamini.com LPF ), 고역통과필터( 하이패스필터. HPF) 판별및 차단 주파수 암기법 – 2차 저역통과필터 주제에 대한 세부정보를 참조하세요. 수동소자로 구성된 저역 … …
Most searched keywords: Whether you are looking for 2차 저역통과필터 | [전기전자 강의] 연산 증폭기 30. 1차, 2차 저역통과필터( 로우패스필터. Lpf ), 고역통과필터( 하이패스필터. Hpf) 판별및 차단 주파수 암기법 346 개의 새로운 답변이 업데이트되었습니다. – Hu.taphoamini.com LPF ), 고역통과필터( 하이패스필터. HPF) 판별및 차단 주파수 암기법 – 2차 저역통과필터 주제에 대한 세부정보를 참조하세요. 수동소자로 구성된 저역 …
Table of Contents:

2차 저역통과필터 주제에 대한 동영상 보기

d여기에서 [전기전자 강의] 연산 증폭기 30 1차 2차 저역통과필터( 로우패스필터 LPF ) 고역통과필터( 하이패스필터 HPF) 판별및 차단 주파수 암기법 – 2차 저역통과필터 주제에 대한 세부정보를 참조하세요

2차 저역통과필터 주제에 대한 자세한 내용은 여기를 참조하세요

주제와 관련된 이미지 2차 저역통과필터

주제에 대한 기사 평가 2차 저역통과필터

Sallen-key 2차 저역 통과 필터 (셀런키 필터)

[필터연재] 2차 디지털 저역고역 통과필터

수동필터와 능동필터의 차이점

12차 저역고역 통과 필터 레포트

키워드에 대한 정보 2차 저역통과필터

사람들이 주제에 대해 자주 검색하는 키워드 [전기전자 강의] 연산 증폭기 30 1차 2차 저역통과필터( 로우패스필터 LPF ) 고역통과필터( 하이패스필터 HPF) 판별및 차단 주파수 암기법

Sallen-key 2차 저역 통과 필터 (셀런키 필터)

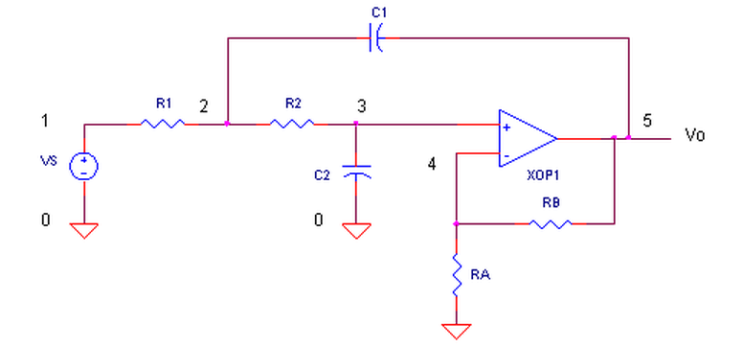
2차 Low pass filter 구조 입니다.

차수는 C의 갯수로 판단해주시면 되고요~!

차단 주파수는 fc = 1/(2*pi*R*C)로 정의가 됩니다.

2차와 차단 주파수의 의미는 보드선도를 그렸을 때,

통과 대역에서 0dB(전압 1배, 그대로 통과를 의미) 를 유지해 주다가 차단 주파수 이전에 서서히 떨어지기 시작하고,

차단 주파수 fc에서 -3dB(전압이 0.707배가 되는)를 기록하고,

보드 선도가 -40dB/decade (주파수 10배 커질 수록 -40dB 감쇄 즉 전압값 0.01배가 되는)를 유지하며 감쇄 비율을 나타 내는 것입니다.

참고로 RC필터에서, 필터 차수 1차당 -20dB/decade를 의미합니다!

OP-AMP 구성 이기 때문에 수동 필터(R,C,L 수동 소자로만 이루어진)가 아닌 능동 필터로써 역할을 해줍니다 ㅎㅎㅎ

뭐 간단히 집고 넘어가자면 수동필터와 능동필터 차이점이 여러가지가 있지만,

능동필터는 TR, OP-AMP등 능동 소자가 들어 갔기 때문에 동작 전원 인가가 별도로 필요 하고, OP-AMP의 대역폭 이상의 대역은 커버 하지 못합니다. 하지만 OP-AMP로 인해 자동적으로 임피던스 매칭이 이루어지면서, 통과 대역의 증폭이 가능 합니다!

위의 그림을 다시 보시면, OP-AMP의 +궤환단에 실질적인 필터가 구성되고, 음의 피드백(-궤환) 단에는 통과대역 이득을 비반전 증폭기 구성과 동일 하게 적용 합니다.

하지만, 주의점은 폐쇄루프이득이 3이상이 되면 발진 합니다.

희한 한 것은 제가 실제로 Sallen-key의 통과 이득을 3이상 주었을 때 발진을 하는 경우도 있었고, 안하는 경우도 있었습니다;;; 여튼 이득이 3일 때 Ringing을 보였고, 그 이상 했을 때 발진을 보이는 경우가 있었습니다.

뭐 여튼!

전달 함수는 밑의 자료를 참고해 주세요!

[필터연재] 2차 디지털 저역/고역 통과필터

1차 저역/고역 통과필터를 디지털로 구현하는 것에 대해 지난번[바로가기]에 이야기를 했었습니다. 저는 거의 대부분의 잡음 제거용 필터는 1차만 사용을 하게 되더군요. 그런데 지금은 연재~^^이니 또 다음으로 Band Pass와 Band Stop 필터도 다룰거라~ 의미상 2차 저역/고역 통과필터도 다룰려고 합니다.^^

일단…

Cut-off 차단 주파수를 결정했다고 하면~

각 주파수를 계산하게 되죠^^

2차는 공진(resonant point)점이 있기 때문에 그 부분을 조절하는 Quality Factor라는 것을 사용합니다. 2차 시스템[바로가기]에서 사용하는 zeta의 역수로 되어 있습니다.

위 식이 2차 저역통과필터의 s-domain에서의 함수입니다.

위 식은 고역통과필터이구요. 두 식이 닮았죠^^.

일단 위 그래프는 같은 2차의 저역/고역 통과필터인데 zeta의 변화에 대한 결과를 보여드리는 겁니다. zeta가 낮을 수록 즉, Q가 높을 수록 차단주파수에서 위로 볼록해집니다. 차단 주파수 대역의 신호를 만나면 증폭(공진)될 수 있겠네요. 또 Phase에서는 zeta가 낮을 수록 가파르게 꺾이게 됩니다.

위 그래프를 그린 Python 코드 확인하기

접기 H0 = 1 zeta = 1 Q = 1 / 2 / zeta num_L2 = np.array([H0 * w_cut * * 2 ]) den_L2 = np.array([ 1 , w_cut / Q, w_cut * * 2 ]) s_L2 = sig.lti(num_L2, den_L2) w_L2, m_L2, P_L2 = sig.bode(s_L2) num_H2 = np.array([H0, 0 , 0 ]) den_H2 = np.array([ 1 , w_cut / Q, w_cut * * 2 ]) s_H2 = sig.lti(num_H2, den_H2) w_H2, m_H2, P_H2 = sig.bode(s_H2) zeta = 0. 1 Q = 1 / 2 / zeta den_2 = np.array([ 1 , w_cut / Q, w_cut * * 2 ]) s_L21 = sig.lti(num_L2, den_2) w_L21, m_L21, P_L21 = sig.bode(s_L21) s_H21 = sig.lti(num_H2, den_2) w_H21, m_H21, P_H21 = sig.bode(s_H21) plt.semilogx(toHz(w_L2), m_L2, lw = 2 , label = ‘2nd LPF $\zeta =1$’ ) plt.semilogx(toHz(w_H2), m_H2, lw = 2 , label = ‘2nd HPF $\zeta =1$’ ) plt.semilogx(toHz(w_L21), m_L21, lw = 1 , ls = ‘dashed’ , label = ‘2nd LPF $\zeta =0.1$’ ) plt.semilogx(toHz(w_H21), m_H21, lw = 1 , ls = ‘dashed’ , label = ‘2nd HPF $\zeta =0.1$’ ) plt.axvline(f_cut, color = ‘k’ , lw = 1 ) plt.xlim( 50 , 15000 ) plt.ylim( – 50 , 20 ) plt.ylabel( ‘Amplitude [dB]’ ) plt.xticks([ 100 , 1000 , 10000 ], ( ” , ‘$f_{cut}$[Hz]’ , ” ), fontsize = 20 ) plt.legend() plt.grid() plt.figure( figsize = ( 12 , 5 )) plt.semilogx(toHz(w_L2), P_L2, lw = 2 , label = ‘2nd LPF $\zeta =1$’ ) plt.semilogx(toHz(w_H2), P_H2, lw = 2 , label = ‘2nd HPF $\zeta =1$’ ) plt.semilogx(toHz(w_L21), P_L21, lw = 1 , ls = ‘dashed’ , label = ‘2nd LPF $\zeta =0.1$’ ) plt.semilogx(toHz(w_H21), P_H21, lw = 1 , ls = ‘dashed’ , label = ‘2nd HPF $\zeta =0.1$’ ) plt.axvline(f_cut, color = ‘k’ , lw = 1 ) plt.xlim( 50 , 15000 ) plt.ylabel( ‘Phase [degree]’ ) plt.legend() plt.xticks([ 100 , 1000 , 10000 ], ( ” , ‘$f_{cut}$[Hz]’ , ” ), fontsize = 20 ) plt.grid() plt.show() 접기

위 그림은 zeta를 1로 고정하고, 같은 차단 주파수에서 1차 저역/고역 통과필터와 비교해본 것입니다. 이득에서는 2차계 필터가 좀 더 가파르게 낮아지기 때문에 차단하고자하는 대역의 주파수 성분의 값이 빨리 사라질 것입니다. phase에서는 1차는 0에서 -90 혹은 90에서 0으로 움직인다면, 2차계 필터는 0에서 -180, 혹은 180에서 0으로 움직이게 됩니다.

위 그림을 그린 Python 코드 보기

접기 num_L1 = np.array([w_cut]) den_L1 = np.array([ 1. , w_cut]) s_L1 = sig.lti(num_L1, den_L1) w_L1, m_L1, P_L1 = sig.bode(s_L1) num_H1 = np.array([ 1. , 0. ]) den_H1 = np.array([ 1. , w_cut]) s_H1 = sig.lti(num_H1, den_H1) w_H1, m_H1, P_H1 = sig.bode(s_H1) H0 = 1 zeta = 1 Q = 1 / 2 / zeta num_L2 = np.array([H0 * w_cut * * 2 ]) den_L2 = np.array([ 1 , w_cut / Q, w_cut * * 2 ]) s_L2 = sig.lti(num_L2, den_L2) w_L2, m_L2, P_L2 = sig.bode(s_L2) num_H2 = np.array([H0, 0 , 0 ]) den_H2 = np.array([ 1 , w_cut / Q, w_cut * * 2 ]) s_H2 = sig.lti(num_H2, den_H2) w_H2, m_H2, P_H2 = sig.bode(s_H2) plt.figure( figsize = ( 12 , 5 )) plt.semilogx(toHz(w_L2), m_L2, lw = 2 , label = ‘2nd LPF’ ) plt.semilogx(toHz(w_H2), m_H2, lw = 2 , label = ‘2nd HPF’ ) plt.semilogx(toHz(w_L1), m_L1, lw = 1 , ls = ‘dashed’ , label = ‘1st LPF’ ) plt.semilogx(toHz(w_H1), m_H1, lw = 1 , ls = ‘dashed’ , label = ‘1st HPF’ ) plt.axvline(f_cut, color = ‘k’ , lw = 1 ) plt.xlim( 50 , 15000 ) plt.ylim( – 50 , 20 ) plt.ylabel( ‘Amplitude [dB]’ ) plt.xticks([ 100 , 1000 , 10000 ], ( ” , ‘$f_{cut}$[Hz]’ , ” ), fontsize = 20 ) plt.legend() plt.grid() plt.figure( figsize = ( 12 , 5 )) plt.semilogx(toHz(w_L2), P_L2, lw = 2 , label = ‘2nd LPF’ ) plt.semilogx(toHz(w_H2), P_H2, lw = 2 , label = ‘2nd HPF’ ) plt.semilogx(toHz(w_L1), P_L1, lw = 1 , ls = ‘dashed’ , label = ‘1st LPF’ ) plt.semilogx(toHz(w_H1), P_H1, lw = 1 , ls = ‘dashed’ , label = ‘1st HPF’ ) plt.axvline(f_cut, color = ‘k’ , lw = 1 ) plt.xlim( 50 , 15000 ) plt.ylabel( ‘Phase [degree]’ ) plt.legend() plt.xticks([ 100 , 1000 , 10000 ], ( ” , ‘$f_{cut}$[Hz]’ , ” ), fontsize = 20 ) plt.grid() plt.show() 접기

이제 s-domain에서 알려진 필터를 디지털 영역인 z-domain으로 데리고 오는 것을 고민해야죠… 뭐 그러나~~~ 이미 교과서(^^)에 있습니다.^^.

이름은 Bilinear Transform[바로가기]이라고 하구요. 위 식을 변환식으로 사용하면 됩니다.

그러면 2차 저역통과필터의 z-domain에서의 표현은 위와 같고,

고역통과필터는 위와 같습니다. 좀 복잡한가요?^^

위 그림과 같은 direct2form의 필터에 사용하기 위해

이런 일반화식에 적용할려고 하면 각 계수들만 알면 되겠죠^^

LPF의 경우는 위의 식이 될 것이고~

HPF의 경우는 위의 식이 될 겁니다.^^ 위 두 공식을 이용해서 필터계수를 계산하는 코드는

def get2ndFilterCoeffi ( f_cut , ts , H0 , zeta , isLPF ): from numpy import pi w0 = 2 * pi * f_cut T = ts Q = 1 / 2 / zeta a0_ = 4 / T * * 2 + 2 * w0 / Q / T + w0 * * 2 a1_ = – 8 / T * * 2 + 2 * w0 * * 2 a2_ = 4 / T * * 2 – 2 * w0 / Q / T + w0 * * 2 if isLPF == ‘LPF’ : b0_ = w0 * * 2 * H0 b1_ = 2 * w0 * * 2 * H0 b2_ = H0 * w0 * * 2 if isLPF == ‘HPF’ : b0_ = 4 * H0 / T * * 2 b1_ = – 8 * H0 / T * * 2 b2_ = 4 * H0 / T * * 2 return a1_ / a0_, a2_ / a0_, b0_ / a0_, b1_ / a0_, b2_ / a0_

로 구현할 수 있겠죠… a0는 어차피 1로 만들거라 위와 같이 하면 되겠습니다. 이제 지난번에도 사용했던 시험신호를 가지고 오면~~

요랬습니다.^^ 이 신호는

이런 주파수 특성을 가지게 만들었죠^^

위 시험신호를 만드는 Python 코드 보기

접기 # Create Test Signal Fs = 10 * 10 * * 3 # 10kHz Ts = 1 / Fs # sample Time endTime = 1 t = np.arange( 0.0 , endTime, Ts) inputSig = 3. * np.sin( 2. * np.pi * t) sampleFreq = np.arange( 10 , 500 , 50 ) for freq in sampleFreq: inputSig = inputSig + 2 * np.sin( 2 * np.pi * freq * t) plt.figure( figsize = ( 12 , 5 )) plt.plot(t, inputSig) plt.xlabel( ‘Time(s)’ ) plt.title( ‘Test Signal in Continuous’ ) plt.grid( True ) plt.show() draw_FFT_Graph(inputSig, Fs, title = ‘inputSig’ , xlim = ( 0 , 600 )) 접기

a1, a2, b0, b1, b2 = get2ndFilterCoeffi( 200 , Ts, 1 , 1 , ‘LPF’ ) dataLPF2 = d2f_2nd(inputSig, a1, a2, b0, b1, b2 ) draw_FFT_Graph(dataLPF2, Fs, title = ‘data_2ndLPF’ , xlim = ( 0 , 600 ))

위 코드를 사용해서 2차 저역통과필터를 차단주파수 200Hz에서 설정해서 FFT 결과를 보면

이렇습니다. 이 결과는 아래 1차와 비교하면…

이렇게 됩니다. 1차때와 비교하면 좀 더 가빠르게 신호들을 제거해 갔다는 것을 알 수 있죠….

원신호와 1차 LPF, 2차 LPF를 보면 결과를 비교해볼 수 있습니다. 같은 설정에서 HPF를

a1, a2, b0, b1, b2 = get2ndFilterCoeffi( 200 , Ts, 1 , 1 , ‘HPF’ ) dataHPF2 = d2f_2nd(inputSig, a1, a2, b0, b1, b2 ) draw_FFT_Graph(dataHPF2, Fs, title = ‘data_2ndLPF’ , xlim = ( 0 , 600 ))

설정해서 결과를 보면…

이렇게 만들어지고~~

Time domain에서 보면.. 1차와의 차이가 보이실 겁니다.^^ 오늘 다룬 코드도 Github[바로가기]에 전체 코드가 공개되어 있습니다.

반응형

1,2차 저역고역 통과 필터 레포트

소개글 예비레포트

목차 없음

본문내용 Low-Pass Filter[LPF]-연산 증폭기에 대하여 저항(R)은 직렬로, 커패시터(C)는 병렬로 연결하여 구성.

-가장 간단한 형태로 구현되어 모든 필터의 기본형으로 쓰임.

-주어진 차단 주파수 보다 낮은 주파수 대역은 통과시키고, 이보다 높은 주파수 대역은 감쇠시킴.(고주파 차단 필터, 적분기 역할)

First – order LPF

저주파에서 커패시터는 개방회로로 동작하여 주파수가 증가함에 따라 전압이득이 감소하게 되고, 주파수가 무한대에 다다르게 되면 전압이득은 거의 0이 된다.

즉, 고주파수가 모두 커패시터 쪽으로 빠져나가고 저주파수는 저항 쪽으로 흐르게 된다.

Second – order LPF

2개의 커패시터는 모두 개방되어 전압플로어로 동작한다. 2개의 커패시터 때문에 이득의 감소는 1차필터보다 2배 빠르다.

-입력신호에 섞인 노이즈(리플, 고주파)를 제거하여 출력신호를 평활화하는 용도로 사용.

*회로의 전압이득과 차단 주파수는 1차 회로와 2차 회로에서 모두 같고,

다만 필터회로의 응답이 2차 회로에서 더 빠른 비율로 감소한다. 즉 2차 필터 회로에서 감소율이 더 높다.

High-Pass Filter[HPF]

So you have finished reading the 2 차 저역 통과 필터 topic article, if you find this article useful, please share it. Thank you very much. See more: 2차 저역통과필터 해석, 1차 2차 저역통과필터, 2차 저역통과필터 전압이득, 3차 저역 통과 필터, 2차 저역통과필터 차단주파수, 2차 필터, 2차 저역통과필터 전달함수, 2차 수동 필터

Top 46 2 차 저역 통과 필터 Top Answer Update

Sallen-key 2차 저역 통과 필터 (셀런키 필터) : 네이버 블로그

2 차 저역 통과 필터

2 차 저역 통과 필터

2 차 저역 통과 필터

2 차 저역 통과 필터

2차 저역통과필터 | [전기전자 강의] 연산 증폭기 30. 1차, 2차 저역통과필터( 로우패스필터. Lpf ), 고역통과필터( 하이패스필터. Hpf) 판별및 차단 주파수 암기법 346 개의 새로운 답변이 업데이트되었습니다. – Hu.taphoamini.com

[필터연재] 2차 디지털 저역/고역 통과필터

필터 구분

1,2차 저역고역 통과 필터 레포트

Sallen-key 2차 저역 통과 필터 (셀런키 필터)

[필터연재] 2차 디지털 저역/고역 통과필터

1,2차 저역고역 통과 필터 레포트

Leave a Comment Cancel reply