You are looking for information, articles, knowledge about the topic nail salons open on sunday near me 식 영어 로 on Google, you do not find the information you need! Here are the best content compiled and compiled by the Chewathai27.com/to team, along with other related topics such as: 식 영어 로 식 영어로 수학, 이름 식 영어로, 공식 영어로, 방정식 영어로, 부등식 영어로, 실근 영어로, 계산식 영어로, 다항식 영어로
[어휘] 수학에서 쓰는 용어들을 영어로 바꿔 보았습니다. : 네이버 블로그
- Article author: m.blog.naver.com
- Reviews from users: 41857
Ratings
- Top rated: 4.2
- Lowest rated: 1
- Summary of article content: Articles about [어휘] 수학에서 쓰는 용어들을 영어로 바꿔 보았습니다. : 네이버 블로그 식(式) expression. 신뢰구간 confence interval. 실근(實根) real root. 실수(實數) real number. 십진법(十進法) decimal system. …
- Most searched keywords: Whether you are looking for [어휘] 수학에서 쓰는 용어들을 영어로 바꿔 보았습니다. : 네이버 블로그 식(式) expression. 신뢰구간 confence interval. 실근(實根) real root. 실수(實數) real number. 십진법(十進法) decimal system.
- Table of Contents:
카테고리 이동
가다 보면 길이 생긴다
이 블로그
영어
카테고리 글
카테고리
이 블로그
영어
카테고리 글
![[어휘] 수학에서 쓰는 용어들을 영어로 바꿔 보았습니다. : 네이버 블로그](https://blogimgs.pstatic.net/nblog/mylog/post/og_default_image_160610.png)
식 영어로 – 식 영어 뜻
- Article author: ko.ichacha.net
- Reviews from users: 1277
Ratings
- Top rated: 4.2
- Lowest rated: 1
- Summary of article content: Articles about
식 영어로 – 식 영어 뜻
식 [式]1 [의식] a ceremony; rituals; rites(종교상의); <집합적> rituals; a (ceremonial) functions; a celebration; an observance; <美> exercises. … - Most searched keywords: Whether you are looking for
식 영어로 – 식 영어 뜻
식 [式]1 [의식] a ceremony; rituals; rites(종교상의); <집합적> rituals; a (ceremonial) functions; a celebration; an observance; <美> exercises. 식 영어로: 식 [式]1 [의식] a ceremony; rituals; rites(종…. 자세한 영어 의미 및 예문 보려면 클릭하십시오식 영어로, 식 영어 뜻 - Table of Contents:

수학식 영어로 읽기 – 영어 – 발효 인문학, 읽나바
- Article author: m.cafe.daum.net
- Reviews from users: 39586
Ratings
- Top rated: 4.0
- Lowest rated: 1
- Summary of article content: Articles about 수학식 영어로 읽기 – 영어 – 발효 인문학, 읽나바 수학식 영어로 읽기. X4 + Y3 = Z : X to the fourth plus Y to the third equals Z. 3(X+4Y)/(X+Y) = Z : Three multiplied by X plus four Y … …
- Most searched keywords: Whether you are looking for 수학식 영어로 읽기 – 영어 – 발효 인문학, 읽나바 수학식 영어로 읽기. X4 + Y3 = Z : X to the fourth plus Y to the third equals Z. 3(X+4Y)/(X+Y) = Z : Three multiplied by X plus four Y … 모든 이야기의 시작, Daum 카페
- Table of Contents:
영어
카페 검색
라쿤잉글리시 – 수학식(덧셈, 뺄셈, 나눗셈, 곱셈) 영어로 읽는 방법
- Article author: raccoonenglish.tistory.com
- Reviews from users: 44517
Ratings
- Top rated: 3.2
- Lowest rated: 1
- Summary of article content: Articles about 라쿤잉글리시 – 수학식(덧셈, 뺄셈, 나눗셈, 곱셈) 영어로 읽는 방법 수학식(덧셈, 뺄셈, 나눗셈, 곱셈) 영어로 읽는 방법 ; - : subtract – 빼다 ; ÷ : dive – 나누다 ; × : multiply – 곱하다. …
- Most searched keywords: Whether you are looking for 라쿤잉글리시 – 수학식(덧셈, 뺄셈, 나눗셈, 곱셈) 영어로 읽는 방법 수학식(덧셈, 뺄셈, 나눗셈, 곱셈) 영어로 읽는 방법 ; - : subtract – 빼다 ; ÷ : dive – 나누다 ; × : multiply – 곱하다. 수학식 (덧셈, 뺄셈, 나눗셈, 곱셈) 영어로 읽는 방법 라쿤잉글리시 미친너굴입니다. 오늘은 우리가 대체로 너무 싫어하는 기본적인 수학식 덧셈, 뺄셈, 나눗셈, 곱셉을 읽고 쓰는 법을 알아보겠습니다. Math Mat..
- Table of Contents:

http://Hybridego.net/ :: 수학식 영어로 읽기
- Article author: hybridego.net
- Reviews from users: 20582
Ratings
- Top rated: 3.8
- Lowest rated: 1
- Summary of article content: Articles about http://Hybridego.net/
:: 수학식 영어로 읽기 다음의 식을 영어로. 요렇게 생긴 것들은 어떻게 읽나요? 제일 앞쪽의 사인함수 적분은 어느정도 답이 나온것 같습니다. 사용자 삽입 이미지. … - Most searched keywords: Whether you are looking for http://Hybridego.net/
:: 수학식 영어로 읽기 다음의 식을 영어로. 요렇게 생긴 것들은 어떻게 읽나요? 제일 앞쪽의 사인함수 적분은 어느정도 답이 나온것 같습니다. 사용자 삽입 이미지. 질문 방정식 같은건 어떻게 영어로 읽나요? X4 + Y3 = Z 3(X+4Y)/(X-Y) = Z 이런것을 어떻게 읽죠? 요새 보는 HowToSolveIt에 심심찮게 방정식이 나오는데 영어로 쭉 읽어 가다가 이런 방정식에서 한글로 읽으려니.. - Table of Contents:
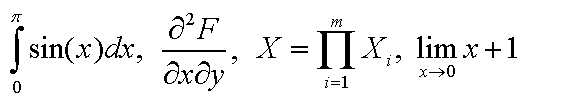 Read More
Read More
식 영어 로
- Article author: www.boardingschool.co.kr
- Reviews from users: 47307
Ratings
- Top rated: 3.5
- Lowest rated: 1
- Summary of article content: Articles about 식 영어 로 Translate [change, convert] each fraction to a decimal : 각각의 분수를 소수로 바꾸시오 – Evaluate each expression : 각각의 식을 계산하시오 …
- Most searched keywords: Whether you are looking for 식 영어 로 Translate [change, convert] each fraction to a decimal : 각각의 분수를 소수로 바꾸시오 – Evaluate each expression : 각각의 식을 계산하시오
- Table of Contents:

영어식 사고 무작정 따라하기 – 박만규 – Google Sách
- Article author: books.google.com.vn
- Reviews from users: 40397
Ratings
- Top rated: 3.4
- Lowest rated: 1
- Summary of article content: Articles about 영어식 사고 무작정 따라하기 – 박만규 – Google Sách Updating …
- Most searched keywords: Whether you are looking for 영어식 사고 무작정 따라하기 – 박만규 – Google Sách Updating 한국인들이여 영어로 말하고 싶다면 단어나 문법 그만 공부하고, ‘영어식 사고법’을 익혀라!우리나라 사람들은 왜 말하기에 취약할까요? 단어나 문법을 몰라서? 아닙니다!영어를 말할 때도 ‘영어식 원리’가 아닌 ‘한국어식 원리’를 적용하기 때문입니다.예를 들어, ‘여기 신용카드 되나요?’를 ‘한국어식 원리’에 그대로 적용해 Is credit card possible?이라고 하면 문법상으로는 맞지만, 네이티브들은 쓰지 않는 표현이 됩니다. 대신 Do you take credit card?라고 물어봐야 합니다. 우리말에는 상대방에게 ‘당신’을 주어로 말하는 게 매우 어색하지만, 영어에서는 상대방에게 ‘you’를 주어로 즐겨 사용하기 때문이죠.그러므로 제대로 된 영어를 말하기 위해서는 더 이상 단어나 문법에 목매지 말고, 발상을 바꿔 ‘영어식 사고법’을 익혀야 합니다! 아래의 딱 6가지 원리만 알면 우리말이 곧바로 쉽고 자연스러운 영어가 됩니다! 당신의 두뇌가 ‘영어식’으로 바뀝니다!원리 1. 사람을 주어로 말하자.원리 2. 동사 have로 말하자.원리 3. 포괄적인 동사로 말하자.원리 4. 전치사로 말하자.원리 5. 최대한 간단하게 말하자.원리 6. 문형을 바꾸어 말하자.‘영어식 사고’가 중독될 때까지 훈련시켜 준다! 자전거 타는 이론만 알면 자전거를 잘 탈 수 있을까요? 이론보다 더 중요한 건, 충분한 훈련입니다. 이론을 바탕으로 열심히 자전거 타는 연습을 해야 비로소 자전거를 탈 수 있습니다!영어도 마찬가지입니다!‘영어식 사고법’이라는 6개의 원리를 머리로 익히고, 문장으로 충분히 훈련해야 영어로 말할 수 있습니다! 이 책은 눈으로 읽는 책이 아닙니다. 연필을 들고 열심히 훈련해야 하는 책입니다. 이 책을 펴는 순간부터 700여 개의 문장이 기다리고 있을 것입니다. 한국인을 위한 본격 ‘스피킹 훈련서’를 만나보세요!
- Table of Contents:
영어로 읽는 세계 롤모델 50인 vol.1: 문학/예술/사회 편 (MP3 무료제공) – 재키 신 – Google Sách
- Article author: books.google.com.vn
- Reviews from users: 31297
Ratings
- Top rated: 4.9
- Lowest rated: 1
- Summary of article content: Articles about 영어로 읽는 세계 롤모델 50인 vol.1: 문학/예술/사회 편 (MP3 무료제공) – 재키 신 – Google Sách Updating …
- Most searched keywords: Whether you are looking for 영어로 읽는 세계 롤모델 50인 vol.1: 문학/예술/사회 편 (MP3 무료제공) – 재키 신 – Google Sách Updating 영어로 읽는『세계 롤모델 50인』제1권 <문학 예술 사회 편>. 이 책은 세계 롤모델 이야기를 영어 원문으로 수록하고 청크(chunk) 영어 학습법과 영어 단어 한글 발음기호를 사용하여 쉽게 공부할 수 있게 만든 자기주도 영어 학습서이다. 청소년들이 미래를 꿈꾸며 장래의 목표를 설정하는 데 바람직한 영향을 줄 수 있는 전 세계 여러 분야에서 두각을 나타낸 롤 모델 50인의 이야기로 구성하였다. 제1권에서는 문학, 예술, 사회에 관련된 인물 25인의 이야기를 다루고 있다.
- Table of Contents:
영어로 읽는 세계 롤모델 50인 vol.2: 정치/과학 기술/스포츠 연예 편 (MP3 무료제공) – 재키 신 – Google Sách
- Article author: books.google.com.vn
- Reviews from users: 27020
Ratings
- Top rated: 3.1
- Lowest rated: 1
- Summary of article content: Articles about 영어로 읽는 세계 롤모델 50인 vol.2: 정치/과학 기술/스포츠 연예 편 (MP3 무료제공) – 재키 신 – Google Sách Updating …
- Most searched keywords: Whether you are looking for 영어로 읽는 세계 롤모델 50인 vol.2: 정치/과학 기술/스포츠 연예 편 (MP3 무료제공) – 재키 신 – Google Sách Updating 국내 최초 세계 롤모델 이야기(영어 원문)를 청크(CHUNK) 영어 학습법과 영어 단어 한글 발음기호를 사용하여 쉽게 공부할 수 있게 만든 자기주도 영어 학습서! 세계 롤모델 50인의 흥미롭고 감동적인 삶과 그들이 이룬 업적에 대해 읽으면서 청소년들이 학습동기와 확실한 비전을 갖게 되고 장래에 대한 목표를 세우는 계기가 됩니다.
- Table of Contents:
네이티브 영어표현력 사전 – 이창수 – Google Sách
- Article author: books.google.com.vn
- Reviews from users: 19613
Ratings
- Top rated: 3.9
- Lowest rated: 1
- Summary of article content: Articles about 네이티브 영어표현력 사전 – 이창수 – Google Sách Updating …
- Most searched keywords: Whether you are looking for 네이티브 영어표현력 사전 – 이창수 – Google Sách Updating 도서에 포함된 MP3(CD) 음원은 다락원 홈페이지(www.darakwon.co.kr)에서 무료 다운로드 가능합니다. 알고 있던 영어 상식이 완전히 뒤집힌다! 콩글리시와 네이티브 표현의 차이를 결정하는 17개 영어 표현법을 체계적으로 정리한 책! 한국외국어대학교 통 · 번역대학원 한영과 이창수 교수가 네이티브 영어의 핵심으로 뽑은 17개 영어식 표현법을 주제로 상세한 설명과 예문을 수록했다. 이 책은 하나의 예문을 콩글리시/직역/네이티브 표현으로 보여 주어 한눈에 비교할 수 있고, 콩글리시와 직역 표현의 틀린 부분을 자세하고 친절하게 설명한다. 또 같은 상황에서 쓸 수 있는 다른 표현도 함께 수록하여 네이티브식 영어 표현을 풍부하게 익힐 수 있다. PART1 기본 단어 네이티브처럼 사용하기 CHAPTER 1 원어민은 기본 동사로 이런 말까지 표현한다 break call carry catch cut do drop fall get go hit hold keep make 39 pull put run see stand CHAPTER 2 전치사는 이렇게 써야 제맛이 난다 above after against at between beyond by from for in into off on out of over through to under with without CHAPTER 3 부사 하나면 어려운 표현이 술술 풀린다 apart around away by down in off out on over through up CHAPTER 4 뭐니 뭐니 해도 구동사가 표현력의 핵심이다 across after along apart around aside away back by down for in into off on out over through to together up PART2 동사,명사와 친해지기 CHAPTER 5 [동사+명사]간 궁합을 모르면 평생 엉터리 영어이다 ⑴ 찰떡궁합 [동사+명사] ⑵ 기본 동사+(동사에서 온) 명사 CHAPTER 6 영어의 길은 동사로 통한다 ⑴ 동사로 부사 표현하기 ⑵ 동사로 비교급 표현하기 ⑶ 동사로 위치 표현하기 CHAPTER 7 이럴 때는 동사보다 명사가 진리다 ⑴ 동사 대신 명사로 표현하기 ⑵ 형용사 대신 명사로 표현하기 CHAPTER 8 여러 품사에서 온 동사는 쓰임새도 화려하다 ⑴ 명사에서 온 동사 ⑵ 형용사/부사에서 온 동사 PART3 주어 선택하기 CHAPTER 9 영어는 주어를 보는 눈이 다르다 CHAPTER 10 무생물 주어를 쓸 수 있어야 콩글리시에서 벗어난다 PART4 영어식으로 생각하기 CHAPTER 11 영어는 영어식 논리로 말해야 빛이 난다 CHAPTER 12 주절주절 긴 표현, 한 단어로 승부하자 CHAPTER 13 수동태는 이렇게 써야 그 진가가 발휘된다 CHAPTER 14 부사를 대신하는 [with+명사]로 영어를 영어답게 말하자 PART5 문장에 화려함 더하기 CHAPTER 15 원어민은 ‘아니다’를 이렇게도 표현한다 ⑴ 부정 접두사, 접미사 ⑵ 부정 의미를 가진 전치사 ⑶ 부정 의미가 담긴 동사 ⑷ last, far, little로 부정 의미를 전달 CHAPTER 16 다양한 강조법으로 문장을 밀고 당겨 보자 ⑴ 긍정 강조 ⑵ 부정 강조 CHAPTER 17 톡 쏘는 비유 표현으로 밋밋한 영어에서 탈출하자 ⑴ a ~ of a … 비유 표현 ⑵ ‘ – ’으로 연결하는 비유 형용사 ⑶ [with+명사+of ] 전치사구
- Table of Contents:
See more articles in the same category here: Chewathai27.com/to/blog.
수학식 영어로 읽기
http://m.blog.naver.com/faithbelief/80012276417
수학식 영어로 읽기
X4 + Y3 = Z : X to the fourth plus Y to the third equals Z.
3(X+4Y)/(X+Y) = Z : Three multiplied by X plus four Y divided by X plus Y equals Z.
X2 : 우리말로 제곱이라고 하고 영어로는 X squared
X3 : 우리말로 세제곱이라고 하는데 입방표시이기도 하므로 X cubed 라는 표현도 가능하고 단순하게 X to the thrid (3rd) 라고도 읽으며
X4 : 네제곱부터는 단순하게 X to the fourth (4th), 5th, 6th, 7th…이런식으로 읽으면 된다고 합니다.
2 x 2 = 4 : two times two equals four / two squared equals four
아인슈타인의 유명한 공식 E=mc2 를 직접 어떻게 읽는지 저자의 육성으로 들어보시지요.
* http://www.aip.org/history/einstein/sound/voice1.wav
“It followed from the special theory of relativity that mass and energy are both but different manifestations of the same thing — a somewhat unfamilar conception for the average mind. Furthermore, the equation E is equal to m c-squared, in which energy is put equal to mass, multiplied by the square of the velocity of light, showed that very small amounts of mass may be converted into a very large amount of energy and vice versa. The mass and energy were in fact equivalent, according to the formula mentioned before. This was demonstrated by Cockcroft and Walton in 1932, experimentally.”
제곱근
√x = square root of x = radical x
3√x = cubic root of x
4√x = fourth root of x
n√x = nth root of x
분수
1/2 = a(one) half, 3/2 = three halves
1/4 = a(one) quarter, 3/4 = three quaters
3/5 = three fifths
m/n = m over n
분모; denominator 분자;numerator
소수
3.14 = three point one four
0.5 = point five
0.05 = point o(zero) five
자주 사용되는 표현
plug in ; 대입하다
substitute
replace
factor out ; 인수분해하다
multiply out ; 전개하다.
use common denominator ; 통분하다.
cancell it out ; 지우다.
take the derivative with respect to x ; x에 관해 미분하다.
differentiate ; 미분하다.
system of linear equations ; 연립방정식
conjugate pair ;
polynomial: 다항식
perimeter: 둘레
수학 용어
자연대수 e(=2.718…)가 들어간 경우, 그냥 발음대로 읽으면 됩니다.
Logarithm이 들어간 경우는, 그냥 우리가 배웠듯이 그냥 log라고 읽으면 됩니다.
허수인 i의 경우도 그냥 발음그대로 읽으면 됩니다.
좀 복잡한 경우를 생각해보면, ei의 경우는 e to the i
벡터의 내적은 inner product 또는 scalar product(ususally Dot product), 벡터의 외적은 outer product, vector product(usually cross product)
삼각함수는 Trigonometric_function
f(x)의 경우는 f of x
수열(Progressionor Sequence)에서 사용하는 등차수열은 Arithmetic Progression, 등비수열은 Geometric Progression, 조화수열은 Harmonic Progression, ∑의 경우는 Summation
급수(수열의 그 항까지의 합)는 Series, 보통 멱급수는 Power Series
소수(2, 3, 5,…): Prime Number, 실수: Real Number, 허수 : Imanginary Number, 자연수 : Natural Number, 유리수 : Rational Number, 무리수 : Irrational Number, 복소수 : Complex Number, 역수 : Reciprocal Number
집합: Set, 교집합: Intersection, 합집합: Union, 차집합 표현 : A – B A Difference B * 방정식 : Equation, 일차방정식 : First Order Equation, 이차방정식 : Second Order Equation, 삼차방정식 : Third Order Equation
무한대: Infinity
무한소: Infinitesimal
대수학: Algebra
선형 대수: Linear Algebra
미적분 : Calculus (미분: differentiation, 적분: integration)
해석학: Analysis
이차방정식은 quadratic equation이라고 보통 쓰던데…
이차방정식에서 X의 0값을 구하는 공식을 quadratic fomula 라고 하고요,
ngative “b” plus minus square root of “b”square minus four “a””c” all over two “b”라고 읽고..
AP Calculus를 배우고 있어서 뭔가 조금 덧붙일 자신있어서 보니까
대부분 다 설명을 해주셨네요… calculus용어를 덧붙이자니 한글로 배운적이 없어서
적당한 용어가 생각이 안나는 “역효과”가… 에구..
상수 e를 특별히 불러 주기 위해서 “constant e”라고도 합니다.
“A이면 B이다.” “B if A.” “If A, then B.”
“A와 B가 동치일 때에는 if 대신 “if and only if”라는 표현을 쓰는데, iff라고도 합니다.
영어 몰입교육이 나라 안을 뒤집어 놓았다. 수학까지 꼭 영어로 배워야 하는지에 대한 답은 저마다 다를 것이다. 아무튼 궁금한 사람들도 많을테니 이것 저것 적어보자.
분수(fraction)를 읽을 때는 분자(numerator)를 기수로 먼저 읽고 분모(denominator)를 서수로 읽는다. 2323는 two third로 읽는다. 그러나 이렇게 읽는 것은 초등학교 산수시간에나 읽는 방법이다. 12131213와 같은 것을 읽는 것은 생각보다 귀찮은 일이다. 그래서 수학에서는 two over three라고 읽는다. 비슷한 모양인데 x+2x−3x+2x−3은 어떻게 읽을까? x plus 2 over x minus 3 으로 읽거나 뜻대로 나누기(divided)를 써서 x plus 2 divided x minus 3으로 읽는다.
limx−>2(x−5)=−3limx−>2(x−5)=−3 을 읽어보자. limit as x goes two x minus five equals negative three로 읽는다. 조심해야할 점은 마이너스 3이 아니라 네가티브 3이라고 읽는 것이다. 빼기와 음수는 다르게 읽는 것이 맞다.
f(x)=x2+3f(x)=x2+3 f of x equals x square plus three
x3+5x−3×3+5x−3 다항식은 polynomial 이다. 지수(exponent)는 서수로 읽어 x to the third plus five x minus three이다.
수학에서 쓰는 말이 일상에서 쓰이기도 하지만 그 뜻이 똑같지는 않다. 또한 영어를 쓰는 사람들 가운데에도 수학 식을 이야기에서 쓰는 일은 거의 없을 것이다. 때문에 수학을 영어로 배운다고 영어를 쓰는 이들과 더 잘 통할 것이라는 생각은 어리석은 것이다. 오히려 더 쉬운 우리말로 풀어내 더 많은 이들이 수학의 나라에 들어설 수 있도록 도와야 할 것이다.
http://Hybridego.net/
* http://www.aip.org/history/einstein/sound/voice1.wav
“It followed from the special theory of relativity that mass and energy are both but different manifestations of the same thing — a somewhat unfamilar conception for the average mind. Furthermore, the equation E is equal to m c-squared , in which energy is put equal to mass, multiplied by the square of the velocity of light, showed that very small amounts of mass may be converted into a very large amount of energy and vice versa. The mass and energy were in fact equivalent, according to the formula mentioned before. This was demonstrated by Cockcroft and Walton in 1932, experimentally.”
· 문제에 잘 나오는 표현들
· 일반적 주요 표현들
· 계산/수/방정식과 부등식/집합과 명제/함수와 그래프/기하/선과 각/다각형/원/입체
· 기타 분야의 용어들
· 수/부호 읽는 법
· 수학에 잘 쓰이는 수 접두사 문제에 잘 나오는 표현들 – What is the value of x? : x의 값은 무엇인가
– Find the shaded area : 빗금친 면적을 구하라
– Solve the equations : 방정식들을 풀어라
– Find the solution : 답을 구하라
– Translate [change, convert] each fraction to a decimal : 각각의 분수를 소수로 바꾸시오
– Evaluate each expression : 각각의 식을 계산하시오
– Simplify : (식을 간단하게 하여)답을 구하라
– Fill in the blank : 빈 칸을 채워라
– Prove [demonstrate] that A=B : A와 B가 같음을 증명하라 일반적 주요 표현들 – X represents [stands for, denotes] the unknown : X는 미지수를 나타낸다
– A corresponds to X : A는 X와 상응한다
– Define : 정의하다 (명: definition)
– Formula : 공식
– Letter : 문자
– Parenthesis : 괄호
– Chart : 도표
– Diagram : 도표, 도형
– Finite : 유한의
– Infinite : 무한의
– Inverse : 반대의, 역의
– Arbitrary : 임의의 (=random)
– Clockwise : 시계 방향으로
– Property : 성질, 속성, 법칙
– Denotation : 표기법
– Approximate : ⓐ대략적인,근사치의 ⓥ근접하다,시키다
– Algebra : 대수
– Geometry : 기하 계산 – Add (명: addition) : 더하다 (명: 덧셈)
– Subtract (명: subtraction) : 빼다 (명: 뺄셈)
– Multiply (명: multiplication) : 곱하다 (명: 곱셈)
– Divide (명: division) : 나누다 (명: 나눗셈)
– x plus y = x increased by y = x added to y : x + y
– x minus y = x decreased by y = y subtracted from x : x – y
– x times y = x multiplied by y : x × y
– Twice (3 times) x : 2(3)x
– X divided by y : x ÷ y
– Bum : 합계
– Product : 곱
– Quotient : (나눗셈의) 몫
– Remainder : (나눗셈의) 나머지
– Fraction : 분수
– Divisor : 나누는 수, 분모: 약수
– Decimal : 소수
– Tenth : 소수 첫째 자리
– Round off : 반올림하다
– Reduce : 약분하다, 떨다
– Reciprocal : 역수(의)
– Mean : 평균 (=average)
– Median : 중위수, 중점, 중선
– Factorize : 인수분해하다
– Prime number : 소수 (약수가 1 혹은 자신 뿐인 수)
– Multiple : 배수
– Greatest common factor : 최대 공약수
– Least common multiple : 최소 공배수
– Exponent : 지수 (x2 에서 2와 같은 것)
– Base : 밑수 (위에서 x와 같은 것)
– Power : 거듭제곱
– Raise : 제곱하다
– x² (읽을 때: x squared) : x 자승 (= x 제곱)
– x³ (읽을 때: x cubed) : x 삼승 (= x 세제곱)
– x⁴(읽을 때: x to the fourth) : x 사승 (= x 사제곱)
– Squared root : 제곱근
– Operation : 계산 수 – Real number : 실수
– Imaginary number : 허수
– Rational number : 유리수
– Irrational number : 무리수
– Integer : 정수
– Even number : 짝수
– Odd number : 홀수
– Positive : 양수의 (반: negative 음수의)
– Nought : 0
– Dozen : 12
– Score : 20
– Binary :2진법의
– Decimal : 10진법의, 소수
– Numeral : 수, 수의 (= numerical) 방정식과 부등식 – Expression : 식
– Term : 식의 항
– Like term : 동류항
– Variable : 변수
– Constant : 상수
– Coefficient : 계수 (3 x² + 5에서 x는 변수, 5는 상수, 3은 계수임)
– Polynomial : 다항식(의)
– Equation : 방정식, 등식
– Simultaneous equations : 연립방정식
– Quadratic equation : 2차 방정식
– Inequality : 부등식
– x is equal to y : x는 y와 같다 (= x equals y = x is y = x is the same as y)
– Equivalent : 동등한
– Add 7 to both sides : 7을 양변에 더하다
– Subtract x from both sides : x를 양변에서 빼다
– Divide both sides by y : y로 양변에서 나누다
– Substitute A for B : B에 A를 대입하다
– Proportion : 비율, 비례
– A is proportional (in proportion) to B : A는 B와 비례한다
– A is inversely proportional to B : A는 B와 반비례한다
– Ratio : 비율
– a is to b as c is to d : a : b = c : d 집합과 명제 – Set : 집합
– Element : 원소
– Intersection : 교집합
– Union : 합집합
– Complement : 여집합
– Subset : 부분집합
– Empty set : 공집합
– Disjoint : 서로 소
– Proposition : 명제
– Statement : 진술
– Theorem : 정리
– False : 그릇된, 허위의 (반: true 참된) 함수와 그래프 – Function : 함수
– Quadrant : 사분면
– Axis : 축
– Coordinates : 좌표
– Ordered pair : 순서쌍
– Intersection : 교점
– Intercept : 절편
– Slope : 기울기
– Liner : 1차의, 직선의
– Horizontal : 수평의
– Vertical : 수직의
– Parallel : 평행의
– Perpendicular : 직각을 이루는
– Convex : 볼록한
– Concave : 오목한
– Parabola : 포물선
– Hyperbola : 쌍곡선 기하 – Plane : 평면
– Figure : 도형, 그림
– Length : 길이
– Width : 너비, 세로
– Height : 높이 (= altitude)
– Side : 변 (비: 삼각형의 옆변은 leg도 됨)
– Base : 밑변
– Area : 면적
– Perimeter : 둘레
– Vertex : 꼭지점
– Solid : 입체
– Edge : 모서리
– Measure : 측정하다
– Bisect : 이등분하다
– Intersect : 교차하다
– Symmetry : 대칭
– Dimension : 차원
– Ruler : 자
– Protractor : 각도기
– Compasses : 콤파스 선과 각 – Line : 선 (특히 끝이 없는 직선)
– Line segment : 선분
– Ray : 반직선 (한쪽만 끝이 있는 직선)
– Oblique : 사선의
– Angle : 각
– Right angle : 직각 (= 900)
– Acute angle : 예각 (900< ) - Obtuse angle : 둔각 (900< x > 1800)
– Vertical angles : 맞꼭지각
– Corresponding angles : 동위각
– Alternate angles : 엇각
– Adjacent angles : 인접각
– Complementary angles : 여각 (인접각의 합이 900인 각)
– Supplementary angles : 보각 (인접각의 합이 1800인 각) 다각형 – Triangle : 삼각형
– Isosceles triangle : 이등변 삼각형
– Equilateral triangle : 정삼각형
– Square : 정사각형
– Rectangle : 직사각형
– Parallelogram : 평행사변형
– Trapezoid : 사다리꼴
– Rhombus : 마름모
– Quadrilateral : (일반) 사각형
– Polygon : 다각형
– Pentagon : 5각형
– Hexagon : 6각형
– Octagon : 8각형
– n-gon : N각형
– Regular polygon : 정다각형
– Diagonal : 대각선
– Interior angle : (다각형의) 내각
– Exterior angle : (다각형의) 외각 원 – Circle : 원
– Diameter : 지름
– Radius : 반지름
– Circumference : 원주
– Chord : 현 (활꼴의 직선부)
– Arc : 호 (활꼴의 곡선부)
– Sector : (원의) 조각, 부채꼴
– Semicircle : 반원
– Tangent : 접하는: 접선
– Secant : 합선
– Ellipse : 타원 입체 – Solid : 입체
– Volume : 부피, 체적
– Capacity : 용량
– Surface : 표면
– Polyhedron : 다면체
– Net : 다면체의 평면도
– Cube : 정육면체
– Rectangular solid : 직육면체
– Pyramid : 사각뿔
– Prism : 삼각기둥
– Cylinder : 원통
– Cone : 원뿔
– Sphere : 구 기타 분야의 용어들 – Calculus : 미적분
– Logarithm : 로그
– Trigonometric function : 삼각함수
– Permutation : 순열
– Combination : 조합
– Probability : 확률
– Statistics : 통계 수/부호 읽는 법 – 1/2 : One half; one over two
– 1/3 : One third; one over three
– 2/3 : Two thirds; tow over three
– 1/4 : One fourth; one over four
– 3/4 : Three fourths; three over four
– 22/3 : Two and two thirds
– 5.164 : Five point one six four
– X : Capital x
– lal : Absolute value of a
– 2a : Two (twice) a
– √a : Square root of a
– 3√a : Cube (cubic) root of a
– n√a : Nth root of a
– a > b : a is greater than b
– a < b : a is less than b - AB∥CD : AB is parallel to CD - AB⊥CD : AB is perpendicular to CD 수학에 잘 쓰이는 수 접두사 어 원 의 미 주요례 hemi, semi 반 (半) hemisphere, semicircle poly 다 (多) polygon deca, deci 10 (1/10) decagon, deciliter (10리터) hect: cent 100 (1/100) centimeter (1/100미터) kilo : mill 1000 (1/1000) millimeter (1/1000미터) mono 1 monomial bi 2 binary tri 3 triple quadr 4 quadrants, quadratic penta 5 pentagon hexa 6 이하 도형 등 hepta 7 이하 도형 등 octa 8 이하 도형 등 ennea 9 이하 도형 등
So you have finished reading the 식 영어 로 topic article, if you find this article useful, please share it. Thank you very much. See more: 식 영어로 수학, 이름 식 영어로, 공식 영어로, 방정식 영어로, 부등식 영어로, 실근 영어로, 계산식 영어로, 다항식 영어로

