You are looking for information, articles, knowledge about the topic nail salons open on sunday near me 산술 기하 평균 증명 on Google, you do not find the information you need! Here are the best content compiled and compiled by the https://chewathai27.com/to team, along with other related topics such as: 산술 기하 평균 증명 산술기하평균 3개, 산술기하평균 조건, 산술기하평균 교육과정, 산술기하 최댓값, 산술기하 부등식, 산술기하평균 활용, 산술기하조화, 산술기하평균 최소값
산술-기하 평균 부등식의 시각적인 증명이다. PR은 중심이 O인 원의 지름이며, 반지름 AO의 길이는 a와 b의 산술 평균이다. 사영 정리를 쓰면, 삼각형 PGR에서 PR을 밑변으로 할 때의 높이 GQ는 기하 평균이다. a:b의 비와 상관 없이, AO ≥ GQ이다.
산술-기하 평균 부등식 – 위키백과, 우리 모두의 백과사전
- Article author: ko.wikipedia.org
- Reviews from users: 48865
Ratings
- Top rated: 4.1
- Lowest rated: 1
- Summary of article content: Articles about 산술-기하 평균 부등식 – 위키백과, 우리 모두의 백과사전 Updating …
- Most searched keywords: Whether you are looking for 산술-기하 평균 부등식 – 위키백과, 우리 모두의 백과사전 Updating
- Table of Contents:
정의[편집]
증명[편집]
관련 정리[편집]
외부 링크[편집]

[기본개념] 산술기하평균 증명과 그 활용
- Article author: bhsmath.tistory.com
- Reviews from users: 21167
Ratings
- Top rated: 4.0
- Lowest rated: 1
- Summary of article content: Articles about [기본개념] 산술기하평균 증명과 그 활용 포스트 내용 산술평균과 기하평균의 관계에 대한 내용입니다. 산술평균과 기하평균의 부등식에 대해서 증명을 그 외 절대부등식과 관련된 내용은 여기 … …
- Most searched keywords: Whether you are looking for [기본개념] 산술기하평균 증명과 그 활용 포스트 내용 산술평균과 기하평균의 관계에 대한 내용입니다. 산술평균과 기하평균의 부등식에 대해서 증명을 그 외 절대부등식과 관련된 내용은 여기 … 포스트 내용 산술평균과 기하평균의 관계에 대한 내용입니다. 산술평균과 기하평균의 부등식에 대해서 증명을 그 외 절대부등식과 관련된 내용은 여기를 클릭 하세요. 산술평균 산술평균이란 그냥 평균이라고..
- Table of Contents:
![[기본개념] 산술기하평균 증명과 그 활용](https://img1.daumcdn.net/thumb/R800x0/?scode=mtistory2&fname=https%3A%2F%2Ft1.daumcdn.net%2Fcfile%2Ftistory%2F261E9A4357EE3CC82F)
절대부등식 증명 – 산술, 기하, 조화평균 – 수학방
- Article author: mathbang.net
- Reviews from users: 4179
Ratings
- Top rated: 4.1
- Lowest rated: 1
- Summary of article content: Articles about 절대부등식 증명 – 산술, 기하, 조화평균 – 수학방 이 절대부등식을 증명할 수 있어야 할 뿐 아니라 공식으로 외워야 합니다. 산술, 기하, 조화평균에 관한 절대부등식이 어떤 것인지, 어떻게 증명하는지, 이 공식을 이용 … …
- Most searched keywords: Whether you are looking for 절대부등식 증명 – 산술, 기하, 조화평균 – 수학방 이 절대부등식을 증명할 수 있어야 할 뿐 아니라 공식으로 외워야 합니다. 산술, 기하, 조화평균에 관한 절대부등식이 어떤 것인지, 어떻게 증명하는지, 이 공식을 이용 … 절대부등식은 항상 성립하는 부등식이라고 했어요. 절대부등식의 종류는 매우 많으니까 굳이 다 알고 있을 필요는 없어요. 하지만 꼭 알고 있어야 하는 절대부등식이 몇 가지 있죠. 바로 산술, 기하, 조화평균에..
- Table of Contents:
절대부등식 증명 – 산술 기하 조화평균
댓글(40개) 펼치기닫기

[부등식] 산술기하평균 부등식 증명, 예제; 산술평균-기하평균 부등식 증명, 예제; 산술기하평균 관계; Arithmetic Mean vs. Geometric Mean : 네이버 블로그
- Article author: m.blog.naver.com
- Reviews from users: 17028
Ratings
- Top rated: 3.4
- Lowest rated: 1
- Summary of article content: Articles about [부등식] 산술기하평균 부등식 증명, 예제; 산술평균-기하평균 부등식 증명, 예제; 산술기하평균 관계; Arithmetic Mean vs. Geometric Mean : 네이버 블로그 [부등식] 산술기하평균 부등식 증명, 예제; 산술평균-기하평균 부등식 증명, 예제; 산술기하평균 관계; Arithmetic Mean vs. Geometric Mean. …
- Most searched keywords: Whether you are looking for [부등식] 산술기하평균 부등식 증명, 예제; 산술평균-기하평균 부등식 증명, 예제; 산술기하평균 관계; Arithmetic Mean vs. Geometric Mean : 네이버 블로그 [부등식] 산술기하평균 부등식 증명, 예제; 산술평균-기하평균 부등식 증명, 예제; 산술기하평균 관계; Arithmetic Mean vs. Geometric Mean.
- Table of Contents:
카테고리 이동
이성근쌤의 메가마인드수학
이 블로그
정의정리공식
카테고리 글
카테고리
이 블로그
정의정리공식
카테고리 글
![[부등식] 산술기하평균 부등식 증명, 예제; 산술평균-기하평균 부등식 증명, 예제; 산술기하평균 관계; Arithmetic Mean vs. Geometric Mean : 네이버 블로그](https://blogthumb.pstatic.net/MjAyMTAyMTdfMiAg/MDAxNjEzNTA2NDgwMDE5.tXQKquzYQY-obQUxNojnwPpSPBIE8H4Lr3oFUukVJDog.VjTbhhYDXAXfhwtHVYR8lQ42NiUK55Y2R-1egU17ro0g.PNG.biomath2k/%B1%D7%B8%B219.png?type=w2)
산술기하 평균(부등식) – 기하적인 방법으로 증명하기
- Article author: ladyang86.tistory.com
- Reviews from users: 17643
Ratings
- Top rated: 4.9
- Lowest rated: 1
- Summary of article content: Articles about 산술기하 평균(부등식) – 기하적인 방법으로 증명하기 절대부등식의 대표적인 예로. 산술기하평균을 이용한 부등식을 배웁니다. 이때, 두 식의 차를 이용하여. 증명하는 것이 가장 일반적이지만,. …
- Most searched keywords: Whether you are looking for 산술기하 평균(부등식) – 기하적인 방법으로 증명하기 절대부등식의 대표적인 예로. 산술기하평균을 이용한 부등식을 배웁니다. 이때, 두 식의 차를 이용하여. 증명하는 것이 가장 일반적이지만,. 절대부등식의 대표적인 예로 산술기하평균을 이용한 부등식을 배웁니다. 이때, 두 식의 차를 이용하여 증명하는 것이 가장 일반적이지만, 기하적인 방법으로도 증명할 수 있습니다. 산술기하 부등식의 조건이 변..30대 수학 강사입니다.
- Table of Contents:
산술기하 평균(부등식) – 기하적인 방법으로 증명하기
티스토리툴바

[수학상 이론 17탄] 산술기하평균의 기하학적 증명 [QR] :: winner
- Article author: j1w2k3.tistory.com
- Reviews from users: 10413
Ratings
- Top rated: 3.3
- Lowest rated: 1
- Summary of article content: Articles about [수학상 이론 17탄] 산술기하평균의 기하학적 증명 [QR] :: winner 산술평균과 기하평균, 조화평균의 대소관계는 일반적인 부등식으로도 증명이 가능하지만, 기하를 이용해서 증명을 하면 기하에서 나오는 여러가지 … …
- Most searched keywords: Whether you are looking for [수학상 이론 17탄] 산술기하평균의 기하학적 증명 [QR] :: winner 산술평균과 기하평균, 조화평균의 대소관계는 일반적인 부등식으로도 증명이 가능하지만, 기하를 이용해서 증명을 하면 기하에서 나오는 여러가지 … 01. 산술평균, 기하평균, 조화평균의 대소관계 증명을 시작하며… 산술평균과 기하평균, 조화평균의 대소관계는 일반적인 부등식으로도 증명이 가능하지만, 기하를 이용해서 증명을 하면 기하에서 나..
- Table of Contents:
티스토리툴바
![[수학상 이론 17탄] 산술기하평균의 기하학적 증명 [QR] :: winner](https://img1.daumcdn.net/thumb/R800x0/?scode=mtistory2&fname=https%3A%2F%2Ft1.daumcdn.net%2Fcfile%2Ftistory%2F1236CD3B50ED914007)
산술 평균, 기하 평균, 조화 평균 – 증명
- Article author: color-change.tistory.com
- Reviews from users: 26099
Ratings
- Top rated: 3.4
- Lowest rated: 1
- Summary of article content: Articles about 산술 평균, 기하 평균, 조화 평균 – 증명 산술 평균, 기하 평균, 조화 평균 – 증명. 들어가며. 산술, 기하, 조화 평균은 절대부등식의 대표적인 예로, 수1 이전 과정뿐만아니라 고2, … …
- Most searched keywords: Whether you are looking for 산술 평균, 기하 평균, 조화 평균 – 증명 산술 평균, 기하 평균, 조화 평균 – 증명. 들어가며. 산술, 기하, 조화 평균은 절대부등식의 대표적인 예로, 수1 이전 과정뿐만아니라 고2, … 산술 평균, 기하 평균, 조화 평균 – 증명 들어가며 산술, 기하, 조화 평균은 절대부등식의 대표적인 예로, 수1 이전 과정뿐만아니라 고2, 고3 수리 영역에서도 단골로 출제되는 소재입니다. (절대부등식이란 특정..
- Table of Contents:
고정 헤더 영역
메뉴 레이어
검색 레이어
상세 컨텐츠
산술 평균 기하 평균 조화 평균 – 증명
정리
추가 정보
페이징

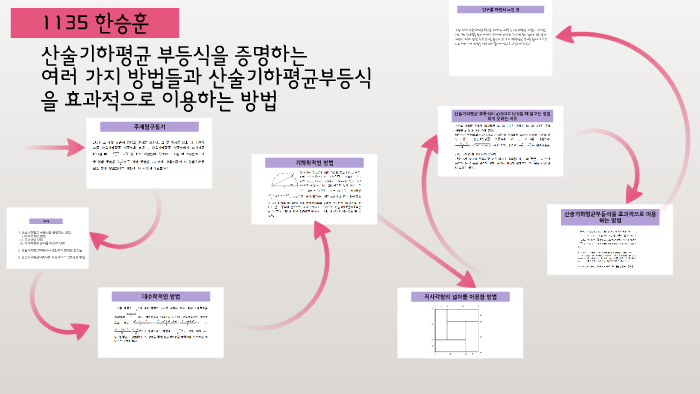
주제: 산술기하평균 부등식을 증명하는 여러 가지 방법들과 산술기하평균부등식을 효과적으로 이용하는 방법 by 승훈 한
- Article author: prezi.com
- Reviews from users: 8783
Ratings
- Top rated: 4.4
- Lowest rated: 1
- Summary of article content: Articles about
주제: 산술기하평균 부등식을 증명하는 여러 가지 방법들과 산술기하평균부등식을 효과적으로 이용하는 방법 by 승훈 한
수업시간에 산술기하평균부등식을 증명하는 방법 중 1번 방법만 배웠다. 하지만, 2번, 3번 증명법을 알아가면서 수학에는 다양한 증명 방법이 있다는 것을 알게 되었다 … … - Most searched keywords: Whether you are looking for
주제: 산술기하평균 부등식을 증명하는 여러 가지 방법들과 산술기하평균부등식을 효과적으로 이용하는 방법 by 승훈 한
수업시간에 산술기하평균부등식을 증명하는 방법 중 1번 방법만 배웠다. 하지만, 2번, 3번 증명법을 알아가면서 수학에는 다양한 증명 방법이 있다는 것을 알게 되었다 … - Table of Contents:
See more articles in the same category here: Top 721 tips update new.
산술-기하 평균 부등식
수학에서, 산술-기하 평균 부등식(算術幾何平均不等式, 영어: arithmetic–geometric mean inequality)은 산술 평균과 기하 평균 사이에 성립하는 부등식이다. 이에 따르면, 임의의 음수가 아닌 실수들에 대하여, 그 산술 평균은 그 기하 평균보다 크거나 같으며, 정확히 모든 실수들이 같은 경우에만 두 평균이 같다.
정의 [ 편집 ]
음이 아닌 실수들 x 1 , x 2 , … , x n ≥ 0 {\displaystyle x_{1},x_{2},\ldots ,x_{n}\geq 0} 이 주어졌다고 하자. 산술-기하 평균 부등식에 따르면, 다음이 성립한다.
x 1 + x 2 + ⋯ + x n n ≥ x 1 x 2 ⋯ x n n {\displaystyle {\frac {x_{1}+x_{2}+\cdots +x_{n}}{n}}\geq {\sqrt[{n}]{x_{1}x_{2}\cdots x_{n}}}}
특히, 등호가 성립할 필요 충분 조건은, 모든 실수들이 같다는 것이다. 즉,
x 1 + x 2 + ⋯ + x n n = x 1 x 2 ⋯ x n n ⟺ x 1 = x 2 = ⋯ = x n {\displaystyle {\frac {x_{1}+x_{2}+\cdots +x_{n}}{n}}={\sqrt[{n}]{x_{1}x_{2}\cdots x_{n}}}\iff x_{1}=x_{2}=\cdots =x_{n}}
증명 [ 편집 ]
귀납적 증명 [ 편집 ]
음이 아닌 실수 x 1 , x 2 , ⋯ , x n ≥ 0 {\displaystyle x_{1},x_{2},\cdots ,x_{n}\geq 0} 및 그 산술 평균
x = x 1 + x 2 + ⋯ + x n n {\displaystyle x={\frac {x_{1}+x_{2}+\cdots +x_{n}}{n}}}
가 주어졌다고 하자. 그렇다면, 산술-기하 평균 부등식은 다음과 같이 쓸 수 있다.
x n ≥ x 1 x 2 ⋯ x n {\displaystyle x^{n}\geq x_{1}x_{2}\cdots x_{n}} x n = x 1 x 2 ⋯ x n ⟺ x 1 = x 2 = ⋯ = x n {\displaystyle x^{n}=x_{1}x_{2}\cdots x_{n}\iff x_{1}=x_{2}=\cdots =x_{n}}
이를 수학적 귀납법으로 증명할 수 있다.
우선, n = 1 {\displaystyle n=1} 인 경우 이는 자명하게 성립한다.
그 다음, n {\displaystyle n} 에 대하여 성립한다는 가정 아래, n + 1 {\displaystyle n+1} 에 대한 산술-기하 평균 부등식
x n + 1 ≥ x 1 x 2 ⋯ x n + 1 {\displaystyle x^{n+1}\geq x_{1}x_{2}\cdots x_{n+1}} x n + 1 = x 1 x 2 ⋯ x n + 1 ⟺ x 1 = x 2 = ⋯ = x n + 1 {\displaystyle x^{n+1}=x_{1}x_{2}\cdots x_{n+1}\iff x_{1}=x_{2}=\cdots =x_{n+1}} x = x 1 + x 2 + ⋯ + x n + 1 n + 1 {\displaystyle x={\frac {x_{1}+x_{2}+\cdots +x_{n+1}}{n+1}}}
을 보이자.
만약 x 1 = x 2 = ⋯ = x n + 1 {\displaystyle x_{1}=x_{2}=\cdots =x_{n+1}} 라면, 자명하게 성립한다. 만약 그렇지 않다면, x {\displaystyle x} 보다 큰 수와 x {\displaystyle x} 보다 작은 수의 쌍이 적어도 하나 존재하며, x n > x > x n + 1 {\displaystyle x_{n}>x>x_{n+1}} 라고 하여도 무방하다. 그렇다면,
( x n − x ) ( x − x n + 1 ) > 0 {\displaystyle (x_{n}-x)(x-x_{n+1})>0}
이다. 또한, 양의 실수
y = x n + x n + 1 − x ≥ x n − x > 0 {\displaystyle y=x_{n}+x_{n+1}-x\geq x_{n}-x>0}
를 정의하면, 다음에 따라, x {\displaystyle x} 는 n {\displaystyle n} 개의 음이 아닌 실수 x 1 , x 2 , … , x n − 1 , y {\displaystyle x_{1},x_{2},\ldots ,x_{n-1},y} 의 산술 평균이기도 하다.
n x = x 1 + x 2 + ⋯ + x n − 1 + x n + x n + 1 − x = x 1 + x 2 + ⋯ + x n − 1 + y {\displaystyle {\begin{aligned}nx&=x_{1}+x_{2}+\cdots +x_{n-1}+x_{n}+x_{n+1}-x\\&=x_{1}+x_{2}+\cdots +x_{n-1}+y\end{aligned}}}
귀납 가정에 따라,
x n + 1 = x n x ≥ x 1 x 2 ⋯ x n − 1 y x {\displaystyle x^{n+1}=x^{n}x\geq x_{1}x_{2}\cdots x_{n-1}yx}
이며, 또한 ①에 따라
y x − x n x n + 1 = ( x n + x n + 1 − x ) x − x n x n + 1 = ( x n − x ) ( x − x n + 1 ) > 0 {\displaystyle yx-x_{n}x_{n+1}=(x_{n}+x_{n+1}-x)x-x_{n}x_{n+1}=(x_{n}-x)(x-x_{n+1})>0}
이므로,
y x > x n x n + 1 {\displaystyle yx>x_{n}x_{n+1}}
이다. ②와 ③에 따라,
x n + 1 = x n x ≥ x 1 x 2 ⋯ x n − 1 y x ≥ x 1 x 2 ⋯ x n − 1 x n x n + 1 {\displaystyle x^{n+1}=x^{n}x\geq x_{1}x_{2}\cdots x_{n-1}yx\geq x_{1}x_{2}\cdots x_{n-1}x_{n}x_{n+1}}
④에서, x > 0 {\displaystyle x>0} 이므로, 만약 x 1 , x 2 , … , x n − 1 {\displaystyle x_{1},x_{2},\ldots ,x_{n-1}} 가운데 0이 있다면, 첫번째 부등호는 등호일 수 없다. 만약에 그들 가운데 0이 없다면, 두번째 부등호는 등호일 수 없다. 이렇게 n + 1 {\displaystyle n+1} 에 대한 산술-기하 평균 부등식이 증명되었다.
코시의 증명 [ 편집 ]
모든 항이 같은 경우 [ 편집 ]
만약
x 1 = x 2 = ⋯ = x n {\displaystyle x_{1}=x_{2}=\cdots =x_{n}}
이라면, 산술 평균과 기하 평균은 x 1 {\displaystyle x_{1}} 로 같다.
모든 항이 같지는 않은 경우 [ 편집 ]
만약 서로 다른 두 항이 존재한다면, 당연히 n > 1 {\displaystyle n>1} 이다.
n = 2 [ 편집 ]
서로 다른 두 항 x 1 , x 2 {\displaystyle x_{1},x_{2}} 가 주어지면,
( x 1 + x 2 2 ) 2 − x 1 x 2 = 1 4 ( x 1 2 + 2 x 1 x 2 + x 2 2 ) − x 1 x 2 = 1 4 ( x 1 2 − 2 x 1 x 2 + x 2 2 ) = ( x 1 − x 2 2 ) 2 > 0 {\displaystyle {\begin{aligned}\left({\frac {x_{1}+x_{2}}{2}}\right)^{2}-x_{1}x_{2}&={\frac {1}{4}}(x_{1}^{2}+2x_{1}x_{2}+x_{2}^{2})-x_{1}x_{2}\\&={\frac {1}{4}}(x_{1}^{2}-2x_{1}x_{2}+x_{2}^{2})\\&=\left({\frac {x_{1}-x_{2}}{2}}\right)^{2}>0\end{aligned}}}
이므로,
x 1 + x 2 2 > x 1 x 2 {\displaystyle {\frac {x_{1}+x_{2}}{2}}>{\sqrt {x_{1}x_{2}}}}
이다.
n = 2k [ 편집 ]
n {\displaystyle n} 이 2의 거듭제곱 꼴인 경우, k {\displaystyle k} 에 대한 수학적 귀납법을 이용하여 증명할 수 있다.
k = 1 {\displaystyle k=1} 인 경우, 즉 n = 2 {\displaystyle n=2} 인 경우는 이미 증명되었다.
k − 1 {\displaystyle k-1} 에 대한 부등식의 가정 아래, k {\displaystyle k} 에 대한 부등식을 보이자.
x 1 + x 2 + ⋯ + x 2 k 2 k = x 1 + x 2 + ⋯ + x 2 k − 1 2 k − 1 + x 2 k − 1 + 1 + x 2 k − 1 + 2 + ⋯ + x 2 k 2 k − 1 2 ≥ x 1 x 2 ⋯ x 2 k − 1 2 k − 1 + x 2 k − 1 + 1 x 2 k − 1 + 2 ⋯ x 2 k 2 k − 1 2 ≥ x 1 x 2 ⋯ x 2 k − 1 2 k − 1 x 2 k − 1 + 1 x 2 k − 1 + 2 ⋯ x 2 k 2 k − 1 = x 1 x 2 ⋯ x 2 k 2 k {\displaystyle {\begin{aligned}{\frac {x_{1}+x_{2}+\cdots +x_{2^{k}}}{2^{k}}}&{}={\frac {{\frac {x_{1}+x_{2}+\cdots +x_{2^{k-1}}}{2^{k-1}}}+{\frac {x_{2^{k-1}+1}+x_{2^{k-1}+2}+\cdots +x_{2^{k}}}{2^{k-1}}}}{2}}\\[7pt]&\geq {\frac {{\sqrt[{2^{k-1}}]{x_{1}x_{2}\cdots x_{2^{k-1}}}}+{\sqrt[{2^{k-1}}]{x_{2^{k-1}+1}x_{2^{k-1}+2}\cdots x_{2^{k}}}}}{2}}\\[7pt]&\geq {\sqrt {{\sqrt[{2^{k-1}}]{x_{1}x_{2}\cdots x_{2^{k-1}}}}{\sqrt[{2^{k-1}}]{x_{2^{k-1}+1}x_{2^{k-1}+2}\cdots x_{2^{k}}}}}}\\[7pt]&={\sqrt[{2^{k}}]{x_{1}x_{2}\cdots x_{2^{k}}}}\end{aligned}}}
여기서 첫번째 부등식에서 등호가 성립하려면, 그 양변에 걸친 두 쌍의 산술 및 기하 평균이 각각 같아야 하므로
x 1 = x 2 = ⋯ = x 2 k − 1 {\displaystyle x_{1}=x_{2}=\cdots =x_{2^{k-1}}} x 2 k + 1 = x 2 k + 2 = ⋯ = x 2 k {\displaystyle x_{2^{k}+1}=x_{2^{k}+2}=\cdots =x_{2^{k}}}
이어야 한다.
두번째 부등식에서 등호가 추가적으로 성립하려면, 그 양변에 걸친 한 쌍의 산술 및 기하 평균이 같아야 한다. 즉, 전반 및 후반 항들의 기하 평균이 서로 같아야 한다. 따라서, 둘 다 등호이려면
x 1 = x 2 = ⋯ = x 2 k {\displaystyle x_{1}=x_{2}=\cdots =x_{2^{k}}}
이어야 한다. 그러나 서로 다른 항이므로, 둘 다 등호일 수 없다. 따라서,
x 1 + x 2 + ⋯ + x 2 k 2 k > x 1 x 2 ⋯ x 2 k 2 k {\displaystyle {\frac {x_{1}+x_{2}+\cdots +x_{2^{k}}}{2^{k}}}>{\sqrt[{2^{k}}]{x_{1}x_{2}\cdots x_{2^{k}}}}}
이다.
n < 2k [ 편집 ] n {\displaystyle n} 이 2의 거듭제곱 꼴이 아닌 경우, n {\displaystyle n} 보다 큰, 2의 거듭제곱 꼴의 수 m {\displaystyle m} 을 취할 수 있다. 음이 아닌 실수 x 1 , x 2 , ⋯ , x n {\displaystyle x_{1},x_{2},\cdots ,x_{n}} 및 그 산술 평균 x {\displaystyle x} 가 주어졌다고 하고, 그 항들을 다음과 같이 m {\displaystyle m} 개로 확장하자. x n + 1 = x n + 2 = ⋯ = x m = x {\displaystyle x_{n+1}=x_{n+2}=\cdots =x_{m}=x} 그렇다면, 이미 증명한 m {\displaystyle m} 에 대한 부등식에 따라, x = x 1 + x 2 + ⋯ + x n n = m n ( x 1 + x 2 + ⋯ + x n ) m = x 1 + x 2 + ⋯ + x n + m − n n ( x 1 + x 2 + ⋯ + x n ) m = x 1 + x 2 + ⋯ + x n + ( m − n ) x m = x 1 + x 2 + ⋯ + x n + x n + 1 + ⋯ + x m m > x 1 x 2 ⋯ x n x n + 1 ⋯ x m m = x 1 x 2 ⋯ x n x m − n m {\displaystyle {\begin{aligned}x&={\frac {x_{1}+x_{2}+\cdots +x_{n}}{n}}\\[6pt]&={\frac {{\frac {m}{n}}(x_{1}+x_{2}+\cdots +x_{n})}{m}}\\[6pt]&={\frac {x_{1}+x_{2}+\cdots +x_{n}+{\frac {m-n}{n}}(x_{1}+x_{2}+\cdots +x_{n})}{m}}\\[6pt]&={\frac {x_{1}+x_{2}+\cdots +x_{n}+(m-n)x}{m}}\\[6pt]&={\frac {x_{1}+x_{2}+\cdots +x_{n}+x_{n+1}+\cdots +x_{m}}{m}}\\[6pt]&>{\sqrt[{m}]{x_{1}x_{2}\cdots x_{n}x_{n+1}\cdots x_{m}}}\\[6pt]&={\sqrt[{m}]{x_{1}x_{2}\cdots x_{n}x^{m-n}}}\end{aligned}}}
따라서,
x m > x 1 x 2 ⋯ x n x m − n {\displaystyle x^{m}>x_{1}x_{2}\cdots x_{n}x^{m-n}}
즉,
x > x 1 x 2 ⋯ x n n {\displaystyle x>{\sqrt[{n}]{x_{1}x_{2}\cdots x_{n}}}}
이다.
미분을 통한 증명 [ 편집 ]
우선, n = 1 , 2 {\displaystyle n=1,2} 인 경우, 산술-기하 평균 부등식은 자명하게 성립한다.
이제, n > 1 {\displaystyle n>1} 에 대하여 성립한다는 가정 아래, n + 1 > 2 {\displaystyle n+1>2} 에 대하여 증명하자. 모든 항이 같은 경우, 산술-기하 평균 부등식은 자명하게 성립한다. 모든 항이 같지는 않을 경우, 당연히 x 1 ≠ x 2 {\displaystyle x_{1}
eq x_{2}} 이라고 전제하여도 무방하다. 이 경우, 다음 식을 증명하여야 한다.
x 1 + ⋯ + x n + x n + 1 n + 1 − ( x 1 ⋯ x n x n + 1 ) 1 n + 1 > 0 {\displaystyle {\frac {x_{1}+\cdots +x_{n}+x_{n+1}}{n+1}}-(x_{1}\cdots x_{n}x_{n+1})^{\frac {1}{n+1}}>0}
이는 음이 아닌 실수 x 1 , … , x n ≥ 0 {\displaystyle x_{1},\dots ,x_{n}\geq 0} 을 고정하고, 함수
f ( t ) = x 1 + ⋯ + x n + t n + 1 − ( x 1 ⋯ x n t ) 1 n + 1 ( t ≥ 0 ) {\displaystyle f(t)={\frac {x_{1}+\cdots +x_{n}+t}{n+1}}-(x_{1}\cdots x_{n}t)^{\frac {1}{n+1}}\qquad (t\geq 0)}
를 정의하였을 때, 다음을 증명하여야 한다는 것과 같다.
f ( x n + 1 ) > 0 {\displaystyle f(x_{n+1})>0}
극값을 구하기 위해, f {\displaystyle f} 의 미분을 취하자.
f ′ ( t ) = 1 n + 1 − 1 n + 1 ( x 1 ⋯ x n ) 1 n + 1 t − n n + 1 {\displaystyle f'(t)={\frac {1}{n+1}}-{\frac {1}{n+1}}(x_{1}\cdots x_{n})^{\frac {1}{n+1}}t^{-{\frac {n}{n+1}}}}
따라서, f {\displaystyle f} 는 다음과 같은 임계점을 갖는다.
f ′ ( t 0 ) = 0 ⟺ t 0 = ( x 1 ⋯ x n ) 1 n {\displaystyle f'(t_{0})=0\iff t_{0}=(x_{1}\cdots x_{n})^{\frac {1}{n}}}
따라서, f {\displaystyle f} 의 가능한 극값은 다음과 같다.
f ( 0 ) = x 1 + ⋯ + x n n + 1 > 0 {\displaystyle f(0)={\frac {x_{1}+\cdots +x_{n}}{n+1}}>0} f ( t 0 ) = x 1 + ⋯ + x n + ( x 1 ⋯ x n ) 1 n n + 1 − ( x 1 ⋯ x n ) 1 n + 1 ( x 1 ⋯ x n ) 1 n ( n + 1 ) = x 1 + ⋯ + x n n + 1 + 1 n + 1 ( x 1 ⋯ x n ) 1 n − ( x 1 ⋯ x n ) 1 n = x 1 + ⋯ + x n n + 1 − n n + 1 ( x 1 ⋯ x n ) 1 n = n n + 1 ( x 1 + ⋯ + x n n − ( x 1 ⋯ x n ) 1 n ) > 0 {\displaystyle {\begin{aligned}f(t_{0})&={\frac {x_{1}+\cdots +x_{n}+({x_{1}\cdots x_{n}})^{\frac {1}{n}}}{n+1}}-({x_{1}\cdots x_{n}})^{\frac {1}{n+1}}(x_{1}\cdots x_{n})^{\frac {1}{n(n+1)}}\\&={\frac {x_{1}+\cdots +x_{n}}{n+1}}+{\frac {1}{n+1}}({x_{1}\cdots x_{n}})^{\frac {1}{n}}-({x_{1}\cdots x_{n}})^{\frac {1}{n}}\\&={\frac {x_{1}+\cdots +x_{n}}{n+1}}-{\frac {n}{n+1}}({x_{1}\cdots x_{n}})^{\frac {1}{n}}\\&={\frac {n}{n+1}}\left({\frac {x_{1}+\cdots +x_{n}}{n}}-({x_{1}\cdots x_{n}})^{\frac {1}{n}}\right)\\&>0\end{aligned}}} lim t → ∞ f ( t ) = ∞ > 0 {\displaystyle \lim _{t\to \infty }f(t)=\infty >0}
여기서, f ( t 0 ) = 0 {\displaystyle f(t_{0})=0} 일 수 없는 이유는, 이미 x 1 ≠ x 2 {\displaystyle x_{1}
eq x_{2}} 이라고 전제하였기 때문이다. 모든 극값이 0보다 크므로, 임의의 t ≥ 0 {\displaystyle t\geq 0} 에 대하여,
f ( t ) > 0 {\displaystyle f(t)>0}
이다. 특히, t = x n + 1 {\displaystyle t=x_{n+1}} 일 경우,
f ( x n + 1 ) > 0 {\displaystyle f(x_{n+1})>0}
이다. 이렇게 n + 1 {\displaystyle n+1} 에 대한 산술-기하 평균 부등식이 증명되었다.
볼록성을 통한 증명 [ 편집 ]
산술-기하 평균 부등식은 양의 실수들 x 1 , x 2 … , x n > 0 {\displaystyle x_{1},x_{2}\dots ,x_{n}>0} 에 대한 다음과 같은 항등식과 동치이다.
ln x 1 + x 2 + ⋯ + x n n > 1 n ( ln x 1 + ln x 2 + ⋯ + ln x n ) ( ¬ x 1 = x 2 = ⋯ = x n ) {\displaystyle \ln {\frac {x_{1}+x_{2}+\cdots +x_{n}}{n}}>{\frac {1}{n}}(\ln x_{1}+\ln x_{2}+\cdots +\ln x_{n})\qquad (\lnot x_{1}=x_{2}=\cdots =x_{n})}
이는 로그 함수의 옌센 부등식이므로, 로그 함수가 엄격 오목 함수임을 보이기만 하면 된다. 이는 이계 도함수 판정법
( ln x ) ″ = ( 1 x ) ′ = − 1 x 2 < 0 ( x > 0 ) {\displaystyle (\ln x)”=\left({\frac {1}{x}}\right)’=-{\frac {1}{x^{2}}}<0\qquad (x>0)}
에 따라 성립한다.
관련 정리 [ 편집 ]
가중 산술-기하 평균 부등식 [ 편집 ]
가중 산술 평균과 가중 기하 평균 사이에도 비슷한 부등식이 성립한다. n개의 음수가 아닌 실수들 x 1 , x 2 , …, x n 과 그에 대응하는 가중치 α 1 , α 2 , …, α n 가 있을 때, 가중치의 합 α = α 1 + α 2 + ⋯ + α n {\displaystyle \alpha =\alpha _{1}+\alpha _{2}+\cdots +\alpha _{n}} 이라 하면 다음이 성립한다.
α 1 x 1 + α 2 x 2 + ⋯ + α n x n α ≥ x 1 α 1 x 2 α 2 ⋯ x n α n α {\displaystyle {\frac {\alpha _{1}x_{1}+\alpha _{2}x_{2}+\cdots +\alpha _{n}x_{n}}{\alpha }}\geq {\sqrt[{\alpha }]{x_{1}^{\alpha _{1}}x_{2}^{\alpha _{2}}\cdots x_{n}^{\alpha _{n}}}}}
마찬가지로 이 부등식은 모든 x k 들이 같을 때 등식이 된다.
가중 산술-기하 평균 부등식의 증명 [ 편집 ]
α k = 0 ( k = 0 , 1 , ⋯ , n ) {\displaystyle \alpha _{k}=0(k=0,1,\cdots ,n)} 를 가중치로 갖는 x k {\displaystyle x_{k}} 은 전체 식에 영향을 주지 않으므로 배제하고 생각하면, 증명에서 다루는 모든 α k {\displaystyle \alpha _{k}} 는 양수라고 가정할 수 있다.
f ( x ) = l n x {\displaystyle f(x)=lnx} 에서 젠센 부등식을 이용하면 쉽게 증명할 수 있다.
x > 0 {\displaystyle x>0} 일 때 f ( x ) = l n x {\displaystyle f(x)=lnx} 는 오목함수, 즉 위로 볼록한 함수이므로
ln ( α 1 x 1 + ⋯ + α n x n α ) > α 1 α ln x 1 + ⋯ + α n α ln x n = ln x 1 α 1 x 2 α 2 ⋯ x n α n α . {\displaystyle {\begin{aligned}\ln {\Bigl (}{\frac {\alpha _{1}x_{1}+\cdots +\alpha _{n}x_{n}}{\alpha }}{\Bigr )}&>{\frac {\alpha _{1}}{\alpha }}\ln x_{1}+\cdots +{\frac {\alpha _{n}}{\alpha }}\ln x_{n}\\&=\ln {\sqrt[{\alpha }]{x_{1}^{\alpha _{1}}x_{2}^{\alpha _{2}}\cdots x_{n}^{\alpha _{n}}}}.\end{aligned}}}
이다. f ( x ) = l n x {\displaystyle f(x)=lnx} 는 단조증가함수이므로
α 1 x 1 + α 2 x 2 + ⋯ + α n x n α ≥ x 1 α 1 x 2 α 2 ⋯ x n α n α {\displaystyle {\frac {\alpha _{1}x_{1}+\alpha _{2}x_{2}+\cdots +\alpha _{n}x_{n}}{\alpha }}\geq {\sqrt[{\alpha }]{x_{1}^{\alpha _{1}}x_{2}^{\alpha _{2}}\cdots x_{n}^{\alpha _{n}}}}}
가 성립함이 증명된다.
제곱-산술-기하-조화 평균 부등식 [ 편집 ]
산술-기하 평균 부등식에 제곱 평균과 조화 평균에 대한 결론을 추가할 수 있다. 음이 아닌 실수 x 1 , x 2 , … , x n ≥ 0 {\displaystyle x_{1},x_{2},\dots ,x_{n}\geq 0} 에 대하여, 다음이 성립한다.
n 1 x 1 + 1 x 2 + ⋯ + 1 x n ≤ x 1 x 2 ⋯ x n n ≤ x 1 + x 2 + ⋯ + x n n ≤ x 1 2 + x 2 2 + ⋯ x n 2 n {\displaystyle {\frac {n}{{\frac {1}{x_{1}}}+{\frac {1}{x_{2}}}+\cdots +{\frac {1}{x_{n}}}}}\leq {\sqrt[{n}]{x_{1}x_{2}\cdots x_{n}}}\leq {\frac {x_{1}+x_{2}+\cdots +x_{n}}{n}}\leq {\sqrt {\frac {x_{1}^{2}+x_{2}^{2}+\cdots x_{n}^{2}}{n}}}}
특히, 각각의 부등호가 등호가 될 성립할 필요 충분 조건은, 모든 실수들이 같다는 것이다. 즉,
n 1 x 1 + 1 x 2 + ⋯ + 1 x n < x 1 x 2 ⋯ x n n < x 1 + x 2 + ⋯ + x n n < x 1 2 + x 2 2 + ⋯ x n 2 n ( ¬ x 1 = x 2 = ⋯ = x n ) {\displaystyle {\frac {n}{{\frac {1}{x_{1}}}+{\frac {1}{x_{2}}}+\cdots +{\frac {1}{x_{n}}}}}<{\sqrt[{n}]{x_{1}x_{2}\cdots x_{n}}}<{\frac {x_{1}+x_{2}+\cdots +x_{n}}{n}}<{\sqrt {\frac {x_{1}^{2}+x_{2}^{2}+\cdots x_{n}^{2}}{n}}}\qquad (\lnot x_{1}=x_{2}=\cdots =x_{n})} n 1 x 1 + 1 x 2 + ⋯ + 1 x n = x 1 x 2 ⋯ x n n = x 1 + x 2 + ⋯ + x n n = x 1 2 + x 2 2 + ⋯ x n 2 n ( x 1 = x 2 = ⋯ = x n ) {\displaystyle {\frac {n}{{\frac {1}{x_{1}}}+{\frac {1}{x_{2}}}+\cdots +{\frac {1}{x_{n}}}}}={\sqrt[{n}]{x_{1}x_{2}\cdots x_{n}}}={\frac {x_{1}+x_{2}+\cdots +x_{n}}{n}}={\sqrt {\frac {x_{1}^{2}+x_{2}^{2}+\cdots x_{n}^{2}}{n}}}\qquad (x_{1}=x_{2}=\cdots =x_{n})} 기타 [ 편집 ] 이 부등식의 다른 일반화된 형태로는 뮤어헤드 부등식과 일반화된 평균 부등식이 있다.
절대부등식 증명 – 산술, 기하, 조화평균
절대부등식은 항상 성립하는 부등식이라고 했어요. 절대부등식의 종류는 매우 많으니까 굳이 다 알고 있을 필요는 없어요.
하지만 꼭 알고 있어야 하는 절대부등식이 몇 가지 있죠. 바로 산술, 기하, 조화평균에 관한 절대부등식이에요. 이 절대부등식을 증명할 수 있어야 할 뿐 아니라 공식으로 외워야 합니다.
산술, 기하, 조화평균에 관한 절대부등식이 어떤 것인지, 어떻게 증명하는지, 이 공식을 이용해서 어떤 문제를 푸는지에 대해서 공부해보죠.
산술, 기하, 조화평균
산술 평균은 시험 점수나 키 평균처럼 우리가 익히 알고 있는 평균을 말해요. 기하평균과 조화평균은 2학년이 되면 공부할 테니까 여기서는 그냥 넘어가고 어떻게 구하는지만 알아봐요.
두 수 a, b의 산술평균 =
두 수 a, b의 기하평균 =
두 수 a, b의 조화평균 =
결론부터 얘기하자면, 이 산술, 기하, 조화평균 사이에는 재미있는 규칙이 있는데, 이 규칙을 부등식으로 나타냈더니 a, b에 상관없이 항상 성립하는 절대부등식이 된 거예요.
a > 0, b > 0일 때
(등호는 a = b일 때 성립)
그리고 중요한 것 한 가지. 이 평균들의 절대부등식을 이용할 때는 숫자들이 모두 양수여야 한다는 거예요.
산술, 기하평균
우선, 산술평균과 기하평균 사이의 관계부터 증명해보죠.
이니까 부등식은 참이 되죠? 그리고 a = b이면 0이 되어 등호가 성립해요.
이 산술, 기하평균을 보면 두 수의 합과 곱으로 되어 있죠? 합이 있는 왼쪽이 더 크거나 같아요. 그래서 이 공식의 특징을 이용해서 합과 곱의 최댓값과 최솟값을 구하는 문제가 많이 나와요.
두 수의 합이 주어졌을 때 곱의 최댓값
두 수의 곱이 주어졌을 때 합의 최솟값
두 분수의 합의 최솟값(두 분수를 곱해서 숫자만 남을 때)
a > 0, b > 0일 때 다음을 구하여라.
(1) a + b = 4일 때 ab의 최댓값
(2) ab = 9일 때 a + b의 최솟값
(3) 의 최솟값
산술, 기하평균 사이의 관계식 의 각 자리에 숫자를 대입하면 돼요. a > 0, b > 0, > 0이에요.
ab는 4보다 작거나 같으므로 두 수의 곱의 최댓값은 4
a + b는 6보다 크거나 같으므로 두 수의 합의 최솟값은 6
(3)번은 두 수의 합의 최솟값을 구하라고 했어요. (2)에서는 합의 최솟값을 구할 때 두 수의 곱을 알려줬는데, 여기서는 알려주지 않았죠? 두 수를 곱하면 문자가 없어지고 숫자만 남아서 곱을 구할 수 있으니까요.
분수면 식이 복잡해지니까 산술, 기하평균의 절대부등식의 모양을 조금 바꿔서 대입해보죠.
위 식에 두 분수를 대입해보죠.
두 분수의 합의 최솟값은
기하, 조화평균
이번에는 기하평균과 조화평균의 관계를 증명해보죠.
a > 0, b> 0일 때 > 0이고 이니까 부등식은 참이죠? 그리고 a = b이면 0이 되어 등호가 성립해요.
기하, 조화평균을 이용한 문제는 별로 나오지 않지만 위 과정을 통해서 증명할 수 있어야 해요.
함께 보면 좋은 글
절대부등식, 부등식의 증명에 이용되는 실수의 성질
코시 슈바르츠 부등식 증명
이차부등식이 항상 성립할 조건
[중등수학/중3 수학] – 대푯값과 평균, 중앙값, 최빈값정리해볼까요 산술, 기하, 조화평균 a > 0, b > 0일 때
(등호는 a = b일 때 성립) 산술, 기하평균을 이용하는 문제 두 수의 합이 주어졌을 때 곱의 최댓값
두 수의 곱이 주어졌을 때 합의 최솟값
두 분수의 합의 최솟값(두 분수를 곱해서 숫자만 남을 때)
그리드형(광고전용)
기하적인 방법으로 증명하기
반응형
절대부등식의 대표적인 예로
산술기하평균을 이용한 부등식을 배웁니다.
이때, 두 식의 차를 이용하여
증명하는 것이 가장 일반적이지만,
기하적인 방법으로도 증명할 수 있습니다.
산술기하 부등식 기하적 증명
산술기하 부등식의 조건이
변수가 모두 양수일 때이므로,
도형에서 변의 길이로 생각하면,
직관적으로 이해가 됩니다.
산술기하 부등식 증명 첫번째
위 그림과 같이 중심이 O이고,
AB를 지름으로 하는 반원을 봅시다.
호 위의 한 점 C를 잡아
수선의 발을 내려줍니다.
양끝으로부터의 길이 중 짧은 것을 a
긴 부분을 b라고 두겠습니다.
그림에서 보면 아시겠지만,
당연히 DO가 CM보다 깁니다.
언제 같을까요?
a=b일때 성립하겠죠.
DO는 원의 반지름이므로 산술평균이고,
CM은 직각삼각형의 높이이므로
기하평균이 나옵니다.
(혹시 이 부분이 바로 나오지 않는다면,
아래 직각삼각형 포스팅을 참고해주세요.
3번째 닮음을 사용하는 부분입니다.)
https://ladyang86.tistory.com/64
아래는 위의 기하적인 증명을 이용한,
교육청 기출문제입니다.
한 번 가볍게 풀어보세요 🙂
정답은 (가) DC (나)EO입니다.
산술기하 부등식 증명 두번째
이번엔 사각형의 넓이를 이용한
보다 직관적인 방법입니다.
도형의 기하적 성질을 이용하면
절대부등식의 증명을 쉽게 할 수 있습니다.
a,b는 둘 다 직사각형의 변의 길이이므로,
자연스럽게 a>0, b>0인 조건이 설정됩니다.
ⓐ 전체 큰 정사각형의 넓이는
ⓑ 안쪽의 붉은색 작은 정사각형의 넓이는
ⓒ 바깥쪽 파란 직사각형 4개의 넓이는
ⓐ=ⓑ+ⓒ입니다.
이 때,
가 성립하므로
임을 알 수 있습니다.
그리고 a>0, b>0이므로 양변에 루트를 씌워도 부등식은 성립합니다.
즉 이런 형태가 되죠. 양변을 2로 나눠서 정리하면 됩니다.
산술평균, 기하평균 외에도
조화평균이 있습니다.
학습량 경감을 이유로
교육과정에서 빠졌죠.
(더불어서 수1의 조화수열도 같이 빠집니다.)
하늘색 부분이 조화평균입니다.
역수가 산술평균을 이루는 수..인데,
교육과정에서 빠졌으니 그냥
저런게 있구나-정도로만 알아도 됩니다.
아니면, 산술평균 부등식을 배운 다음
이걸 위와 같이 기하적으로 증명하고,
심화주제로 조화평균을 같이 다루면
보고서 쓰기에 매우 좋을 거 같긴 하네요.
수학 보고서 주제,
혹은 수학 발표 주제로 추천합니다.
ㅎㅎ
그럼 저는 오늘도 여러분을 응원하며
이만 포스팅을 마치겠습니다.
반응형
So you have finished reading the 산술 기하 평균 증명 topic article, if you find this article useful, please share it. Thank you very much. See more: 산술기하평균 3개, 산술기하평균 조건, 산술기하평균 교육과정, 산술기하 최댓값, 산술기하 부등식, 산술기하평균 활용, 산술기하조화, 산술기하평균 최소값

