Top 32 피어슨 상관계수 공식 22766 Votes This Answer

You are looking for information, articles, knowledge about the topic nail salons open on sunday near me 피어슨 상관계수 공식 on Google, you do not find the information you need! Here are the best content compiled and compiled by the https://chewathai27.com/to team, along with other related topics such as: 피어슨 상관계수 공식 피어슨 상관계수 해석, 피어슨 상관계수 예시, 상관계수 계산기, 상관계수 해석 기준, correlation 상관계수, 상관계수 p값 계산, 피어슨 상관관계 분석, 스피어만 상관계수 공식

Pearson 상관 계수의 경우: H ₀: ρ = 0 대 H ₁: ρ ≠ 0, 여기서 ρ는 변수 쌍 사이의 상관 계수입니다. 작은 p-값은 귀무 가설이 거짓임을 나타냅니다. 상관 계수가 0이 아니고 선형 관계가 존재한다는 결론을 내릴 수 있습니다.

논문통계분석 기초와 논문 작성법 (5) 상관관계분석

ìê´ì ëí ë°©ë² ë° ê³µì – Minitab

Article author: support.minitab.com
Reviews from users: 3115 Ratings
Top rated: 4.3
Lowest rated: 1
Summary of article content: Articles about ìê´ì ëí ë°©ë² ë° ê³µì – Minitab Updating …
Most searched keywords: Whether you are looking for ìê´ì ëí ë°©ë² ë° ê³µì – Minitab Updating ìíë ë°©ë² ëë ê³µìì ì ííììì¤.
Table of Contents:

Pearsonì ìê´ ê³ì

Spearmanì ìê´ ê³ì

P-ê°

ìê´ì ëí ë°©ë² ë° ê³µì – Minitab

Article author: ko.wikipedia.org
Reviews from users: 25489 Ratings
Top rated: 4.7
Lowest rated: 1
Summary of article content: Articles about 피어슨 상관 계수 – 위키백과, 우리 모두의 백과사전 통계학에서 , 피어슨 상관 계수(Pearson Correlation Coefficient ,PCC)란 두 변수 X 와 Y 간의 선형 상관 관계를 계량화한 수치다. 피어슨 상관 계수는 코시-슈바르츠 … …
Most searched keywords: Whether you are looking for 피어슨 상관 계수 – 위키백과, 우리 모두의 백과사전 통계학에서 , 피어슨 상관 계수(Pearson Correlation Coefficient ,PCC)란 두 변수 X 와 Y 간의 선형 상관 관계를 계량화한 수치다. 피어슨 상관 계수는 코시-슈바르츠 …
Table of Contents:

정의[편집]

모집단의 경우[편집]

결정계수[편집]

컴퓨팅 계산[편집]

같이 보기[편집]

참고[편집]

피어슨 상관 계수 - 위키백과, 우리 모두의 백과사전 — 피어슨 상관 계수 – 위키백과, 우리 모두의 백과사전

Article author: codingfarm.tistory.com
Reviews from users: 5955 Ratings
Top rated: 4.0
Lowest rated: 1
Summary of article content: Articles about 피어슨 상관 계수(Pearson Correlation Coefficient) bullet$ (피어슨)상관 계수는 두 변수가 서로 (선형)상관관계를 가지는지 확인하는 척도이다. $\bullet$ 1이나 -1에 가까우면 상관관계가 있다 보고 0 … …
Most searched keywords: Whether you are looking for 피어슨 상관 계수(Pearson Correlation Coefficient) bullet$ (피어슨)상관 계수는 두 변수가 서로 (선형)상관관계를 가지는지 확인하는 척도이다. $\bullet$ 1이나 -1에 가까우면 상관관계가 있다 보고 0 … $\bullet$ (피어슨)상관 계수는 두 변수가 서로 (선형)상관관계를 가지는지 확인하는 척도이다. $\bullet$ 1이나 -1에 가까우면 상관관계가 있다 보고 0이면 없다고 본다. $\bullet$ $[-1,1]$을 벗어나지 않는다…
Table of Contents:

codingfarm

피어슨 상관 계수(Pearson Correlation Coefficient) 본문

Article author: nittaku.tistory.com
Reviews from users: 37595 Ratings
Top rated: 3.8
Lowest rated: 1
Summary of article content: Articles about 4. 상관계수 정리 상관계수(r) 공식 (피어슨 상관계수 – Pearson’s correlation coefficent). 공분산(Covariance) : 두 숫자형 변수가 같은 방향으로 움직이는 정도, … …
Most searched keywords: Whether you are looking for 4. 상관계수 정리 상관계수(r) 공식 (피어슨 상관계수 – Pearson’s correlation coefficent). 공분산(Covariance) : 두 숫자형 변수가 같은 방향으로 움직이는 정도, … 상관계수 정의 숫자형-숫자형 변수의 관계를 파악할 때 : 산점도(그래프) , 상관계수(수치) 숫자형-숫자형 변수간의 강도를 수치로 표현하는 방법 상관계수는 인과성이 아닌 연관성 만 확인가능하다. ( 연관성 안..IT에 관심이 많은 동신대 한의대생의 개발일지
Table of Contents:

Article author: umbum.dev
Reviews from users: 34359 Ratings
Top rated: 3.4
Lowest rated: 1
Summary of article content: Articles about 피어슨 상관 계수 (Pearson Correlation Coefficient) 추천 시스템에서 collaborative filtering 방식을 사용할 때는 User-user 간, 또는 Item-item 간 similarity를 계산해야 한다. 이 때 피어슨 상관 계수를 … …
Most searched keywords: Whether you are looking for 피어슨 상관 계수 (Pearson Correlation Coefficient) 추천 시스템에서 collaborative filtering 방식을 사용할 때는 User-user 간, 또는 Item-item 간 similarity를 계산해야 한다. 이 때 피어슨 상관 계수를 … 상관계수(correlation coefficient)란 두 변수가 어떤 상관 관계를 가지는가?를 의미하는 수치다. +1은 완벽한 양의 선형 상관 관계, 0은 선형 상관 관계 없음, -1은 완벽한 음의 선형 상관 관계를 의미한다. X와..
Table of Contents:

이 글 공유하기

다른 글

Website for public datasets

민감도와 특이도 (sensitivity specificity)

재표본추출 방법 Resampling Methods

분류 Classification

티스토리툴바

Article author: m.blog.naver.com
Reviews from users: 11517 Ratings
Top rated: 3.7
Lowest rated: 1
Summary of article content: Articles about SPSS 피어슨 상관 계수 Pearson Correlation Coefficient, PCC : 네이버 블로그 피어슨 상관계수 계산해서 표로 만들어드립니다. 통계논문 도와드립니다. . 서울대 학사/석사. 미국 주립대 박사. . …
Most searched keywords: Whether you are looking for SPSS 피어슨 상관 계수 Pearson Correlation Coefficient, PCC : 네이버 블로그 피어슨 상관계수 계산해서 표로 만들어드립니다. 통계논문 도와드립니다. . 서울대 학사/석사. 미국 주립대 박사. .
Table of Contents:

카테고리 이동

맛있는 여행

이 블로그
통계학
카테고리 글

카테고리

이 블로그
통계학
카테고리 글

SPSS 피어슨 상관 계수 Pearson Correlation Coefficient, PCC : 네이버 블로그

Article author: kb.tableau.com
Reviews from users: 46481 Ratings
Top rated: 3.1
Lowest rated: 1
Summary of article content: Articles about 피어슨 상관 관계 찾기 | Tableau Software 이 수식은 두 식의 피어슨 상관 계수를 반환합니다. 피어슨 상관 계수는 두 변수 간의 선형 관계를 측정합니다. 결과는 -1에서 +1(포함) 사이이며, 1은 정확한 양의 … …
Most searched keywords: Whether you are looking for 피어슨 상관 관계 찾기 | Tableau Software 이 수식은 두 식의 피어슨 상관 계수를 반환합니다. 피어슨 상관 계수는 두 변수 간의 선형 관계를 측정합니다. 결과는 -1에서 +1(포함) 사이이며, 1은 정확한 양의 …
Table of Contents:

피어슨 상관 관계 찾기

모든 지원

피어슨 상관 관계 찾기 | Tableau Software

Article author: ko.wukihow.com
Reviews from users: 40592 Ratings
Top rated: 3.0
Lowest rated: 1
Summary of article content: Articles about Pearson 상관 계수를 계산하는 방법 Pearson Correlation Coefficient (Pearson Product-Moment Correlation Coefficient)는 1900 년대 초 Karl Pearson에 의해 설정되었습니다. …
Most searched keywords: Whether you are looking for Pearson 상관 계수를 계산하는 방법 Pearson Correlation Coefficient (Pearson Product-Moment Correlation Coefficient)는 1900 년대 초 Karl Pearson에 의해 설정되었습니다. Pearson Correlation Coefficient (Pearson Product-Moment Correlation Coefficient)는 1900 년대 초 Karl Pearson에 의해 설정되었습니다. 사물이 서로 얼마나 밀접하게 관련되어 있는지, 그리고 관계가 어떤 방향으로 가고 있는지 알려줍니다! 공식은 다음과 같습니다. r = Σ (X-Mx) (Y-My) / (N-1) SxSy [1] 엑스 연구 출처
단순화하고 싶습니까? 우리의 가설은 초콜릿의 소비가 증가함에 따라 개인의 행복도도 1 (불행)에서 7 (행복)까지의 척도로 증가한다는 것입니다. 초콜렛을 먹으면 더 행복 해지는 건 다들 아시죠? 시작하기 전에 두 변수 (X 및 Y)를 식별하십시오. 한 사람이 하루에 먹는 초콜릿의 수 (X)와 그들의 행복 수준 (Y)에 대한 정보가 있다고 가정 해 보겠습니다.
Table of Contents:

피어슨 상관 계수

통계학에서 , 피어슨 상관 계수(Pearson Correlation Coefficient ,PCC)란 두 변수 X 와 Y 간의 선형 상관 관계를 계량화한 수치다. 피어슨 상관 계수는 코시-슈바르츠 부등식에 의해 +1과 -1 사이의 값을 가지며, +1은 완벽한 양의 선형 상관 관계, 0은 선형 상관 관계 없음, -1은 완벽한 음의 선형 상관 관계를 의미한다. 일반적으로 상관관계는 피어슨 상관관계를 의미하는 상관계수이다.

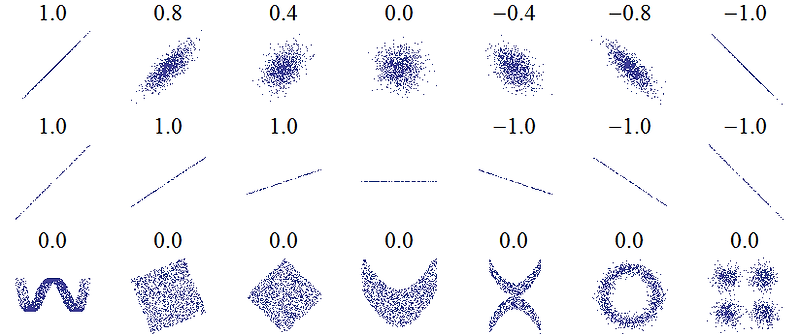
서로 다른 상관 계수 값 (ρ)을 갖는 산포도 다이어그램의 예

x 와 y 의 상관 계수. 상관 관계는 선형 관계의 비선형성 및 방향을 반영하지만 그 관계의 기울기 또는 비선형 관계의 여러 측면을 반영하지 않는다. NB : 중앙의 그림은 기울기가 0이지만이 경우 Y 의 분산이 0이므로 상관 계수가 정의되지 않는다. 여러 데이터셋와 각 셋의의 상관 계수. 상관 관계는 선형 관계의 비선형성 및 방향을 반영하지만 그 관계의 기울기 또는 비선형 관계의 여러 측면을 반영하지 않는다. NB : 중앙의 그림은 기울기가 0이지만이 경우의 분산이 0이므로 상관 계수가 정의되지 않는다.

정의 [ 편집 ]
표본(sample) 피어슨 상관 계수는 등간척도(간격척도)나 비례척도(비율척도)의 데이타에서 두 변수의 공분산(covariance) 을 각각의 표준 편차의 곱으로 나눈 값이다.

피 어 슨 상 관 계 수 = 공 분 산 표 준 편 차 ⋅ 표 준 편 차 {\displaystyle {\text{피 어 슨 상 관 계 수 }}={{\text{공 분 산 }} \over {{\text{표 준 편 차 }}\cdot {\text{표 준 편 차 }}}}} r X Y = ∑ i n ( X i − X ¯ ) ( Y i − Y ¯ ) n − 1 ∑ i n ( X i − X ¯ ) 2 n − 1 ∑ i n ( Y i − Y ¯ ) 2 n − 1 {\displaystyle r_{XY}={{{\sum _{i}^{n}\left(X_{i}-{\overline {X}}\right)\left(Y_{i}-{\overline {Y}}\right)} \over {n-1}} \over {{\sqrt {{\sum _{i}^{n}\left(X_{i}-{\overline {X}}\right)^{2}} \over {n-1}}}{\sqrt {{\sum _{i}^{n}\left(Y_{i}-{\overline {Y}}\right)^{2}} \over {n-1}}}}}}

따라서

r X Y = ∑ i n ( X i − X ¯ ) ( Y i − Y ¯ ) ∑ i n ( X i − X ¯ ) 2 ∑ i n ( Y i − Y ¯ ) 2 {\displaystyle r_{XY}={{\sum _{i}^{n}\left(X_{i}-{\overline {X}}\right)\left(Y_{i}-{\overline {Y}}\right)} \over {{\sqrt {\sum _{i}^{n}\left(X_{i}-{\overline {X}}\right)^{2}}}{\sqrt {\sum _{i}^{n}\left(Y_{i}-{\overline {Y}}\right)^{2}}}}}}

모집단의 경우 [ 편집 ]
피어슨의 상관 계수는 모집단에 적용될 때 일반적으로 ρ (그리스문자,로)로 표시되며 모집단 상관 계수 또는 모집단 피어슨 상관 계수라고 할 수 있다.

결정계수 [ 편집 ]
피어슨의 상관 계수를 제곱해줌으로써 결정계수를 얻을수있다.

표본 피어슨의 상관 계수 r {\displaystyle r} r 2 {\displaystyle r^{2}} 모집단 피어슨의 상관 계수 ρ {\displaystyle \rho } ρ 2 {\displaystyle \rho ^{2}}

컴퓨팅 계산 [ 편집 ]
컴퓨팅 프로그램에서 일반적인 상관관계 분석 함수로서 피어슨 상관계수가 사용되며 스프레드 시트에서는 Correl()함수를 사용할 수 있다.[1] SPSS 및 PSPP에서는 이변량 상관분석(bivariate analysis 또는 bivariate correlation analysis)등에서 보편적으로 이용된다.

같이 보기 [ 편집 ]

피어슨 상관 계수(Pearson Correlation Coefficient)

$\bullet$ (피어슨)상관 계수는 두 변수가 서로 (선형)상관관계를 가지는지 확인하는 척도이다.

$\bullet$ 1이나 -1에 가까우면 상관관계가 있다 보고 0이면 없다고 본다.

$\bullet$ $[-1,1]$을 벗어나지 않는다.

다음과 같이 정의된 $\rho = \rho (X,Y)$ 를 피어스 상관계수(pearson correlation coefficient)라고 한다.

$$\rho = \dfrac{Cov(X,Y)}{\sigma_X \sigma_Y}=\dfrac{\sigma_{XY}}{\sigma_X\sigma_Y},\;\;\;\;\; -1 \leq \rho \leq 1$$

$Cov(X,Y)$를 $X$와 $Y$의 공분산(covariance)라 한다.

$Cov(X,Y) = E[(X-\mu_X)(Y-\mu_Y)]=E(XY)-\mu_X \mu_Y$

$E(XY) = \mu_X \mu_Y + \rho \sigma_X \sigma_Y$

$X$와 $Y$가 독립이면 상관계수는 0이된다.

하지만 상관계수가 0이라고 $X$와 $Y$가 독립인것은 아니다.

$\rho$를 정의한 식에 대해 알아보자

$\mu_X = E(X),\;\; =\mu_Y=E(Y),\;\;\; \sigma_X^2=E[(X-\mu_X)^2],\;\;\;\sigma_Y^2=E[(Y-\mu_Y)^2]$

(a) $u(X,Y) = (X-\mu_X)(Y-\mu_Y)$ 라 두면

$$E[u(X,Y)]=E[(X-\mu_X)(Y-\mu_Y)]=\sigma_{XY}=Cov(X,Y)$$

를 $X$와 $Y$의 공분산(covariance)라 한다.

(b) 표준편차 $\sigma_X, \sigma_Y>0$이라면

$$\rho = \dfrac{Cov(X,Y)}{\sigma_X \sigma_Y}=\dfrac{\sigma_{XY}}{\sigma_X \sigma_Y}$$

를 $X$와 $Y$의 상관계수라 한다.

$X$의 평균(mean)과 분산(variance)는 결합 pmf(or pdf) 혹은 주변 pmf(or pdf)를 이용해서 푼다.

ex) 이산형의 경우

$$\begin{align*}

\mu_X = E(X) & = \sum_X \sum_Y x f(x,y)\\

&=\sum_x x \left[ \sum_y f(x,y) \right] = \sum_x x f_X(x)

\end{align*}$$

공분산(Covariance)의 계산에는 joint pmf(or pdf)가 필요하다

공분산 $E[u(x,y)]$와 상관계수 $\rho = \dfrac{Cov(X,Y)}{\sigma_X \sigma_Y}$의 의미를 살펴보기전 2가지 유용한 식을 유도한다.

1)

$$\begin{align*}

Cov(X,Y) = E[(X-\mu_X)(Y-\mu_Y)]&=E(XY – \mu_X Y -\mu_Y X + \mu_X \mu_Y)\\

&=E(XY)-\mu_XE(Y)-\mu_YE(X)+\mu_X \mu_Y\\

&=E(XY) – \mu_X \mu_Y – \mu_X \mu_Y + \mu_X \mu_Y \\

&= E(XY) – \mu_X \mu_Y

\end{align*}$$

2)

$$\rho = \dfrac{Cov(X,Y)}{\sigma_X \sigma_Y} = \dfrac{E(XY) – \mu_X \mu_Y}{\sigma_X \sigma_Y}$$

$$E(XY) = \mu_X \mu_Y + \rho \sigma_X \sigma_Y$$

즉, 두 확률변수의 곱의 기댓값은 각 확률변수들의 평균(mean)과 편차(deviation)를 통해서 구할 수 있다.

예제 4.2-1 펼치기 예제 4.2-1 접기 예제 4.2-1 접기

두 확률변수 $X$와 $Y$의 상관계수(Correlation Coefficient)$\rho$에 대해 알아보자.

1) $\rho$의 부호

$$\rho = \dfrac{\sum_X\sum_Y(x-\mu_X)(y-\mu_Y)f(x,y)}{\sigma_X \sigma_Y}$$

$\bullet$ 분모는 항상 양수이다.

$\bullet$ $0 \leq f(x,y)\leq 1$ 이다.

$\therefore$ $\rho$의 부호를 결정하는 것은 $x$와 $y$, $\mu_X$, $\mu_Y$이다.

$\rho>0$ $\rho <0$ $\rho=0$ $x$가 $\mu_X$보다 크고 $y$가 $\mu_Y$보다 큰 혹은 $x$가 $\mu_X$보다 작고 $y$가 $\mu_Y$보다 작은 $(x,y)$쌍이 아주 많을 경우 $x$가 $\mu_X$보다 크고 $y$가 $\mu_Y$보다 작은 혹은 $x$가 $\mu_X$보다 작고 $y$가 $\mu_Y$보다 큰 $(x,y)$쌍이 아주 많을 경우 모든 $(x,y)$쌍에 대해 $x= \mu_X$그리고 $y=\mu_Y$일 경우 혹은 모든 항의 합이 0이 될 경우 2) $-1 \leq \rho \leq 1$ 우선 임의의 $(x,y)$쌍들을 그래프 위에 그려보겠다. 수많은 점들의 분포를 일반식으로 간단하게 표현할수는 없다 그렇기에 모든 점들을 근사적으로 표현할 수 있는 직선방정식을 찾도록 한다. 이 방정식을 만드는 기준은 i) $(\mu_X \mu_Y)$를 지난다. ii) 모든 점으로부터의 거리의 평균값이 최소가 되는 기울기 $b$를 가진다. 위 조건을 만족하는 직선 방정식을 적으면 $y=\mu_Y + b(x-\mu_X)$ 이제 ii) 조건에 맞는 $b$를 구하면 된다. 임의의 점 $(x_0,y_0)$에서 직선 방정식 까지의 거리는 $|y_0 - \mu_Y - b(x_0 - \mu_X)|$이다. 이 거리를 제곱한 값들의 평균을 취한 식을 $K(b)$로 지칭한다. $$E\{[(Y - \mu_Y)-b(X - \mu_X)]^2\}=k(b)$$ 최소제곱원리로 $K(b)$를 최소로 하는 $b$값을 찾는다. $$\begin{align*} K(b) &=E[(Y-\mu_Y)^2-2b(X-\mu_X)(Y-\mu_Y)+b^2(X-\mu_X)^2]\\ &=\sigma_Y^2 - 2b \rho \sigma_X \sigma_Y + b^2 \sigma_X^2 \end{align*}$$ 를 $b$로 편미분하여 $0$으로 놓고 $b$를 구한다 $$K'(b) = -2 \rho \sigma_X \sigma_Y + 2b \sigma_X^2=0\\ b = \rho \dfrac{\sigma_Y}{\sigma_X}$$ $K(b)$는 최고차항의 계수가 양수인 $b$에 관한 2차식인데다가 $K''(b) = 2\sigma_X^2 > 0$이므로 위의 $b$는 $K(b)$를 최소로 만드는 식임을 알 수 있다.

따라서 최량 적합 직선(the line of best fit)의 형태인 최소 제곱 회귀 직선(least squares regression line)은

$Y = \mu_Y = \rho \dfrac{\sigma_Y}{\sigma_X}(X – \mu_X)$

가 된다.

여기서 $\rho$의 값에 따라 기울기가 결정된다.

또한 $K(b)$는 제곱의 기댓값이므로 모든 $b$에 대해서 음수가 아니어야 한다. 따라서 최소값도 양수이므로

$$\begin{align*}

K \left( \rho \dfrac{\sigma_Y}{\sigma_X} \right) &= \sigma_Y^2 – 2\rho \dfrac{\sigma_Y}{\sigma_X}\rho \sigma_X \sigma_Y + \left( \rho \dfrac{\sigma_Y}{\sigma_X}\right)^2 \sigma_X^2\\

&=\sigma_Y^2 -2\rho^2\sigma_Y^2 + \rho^2 \sigma_Y^2 = \sigma_Y^2(1 – \rho^2) \geq 0

\end{align*} $$

그러므로 $-1 \leq \rho \leq 1$이 된다.

예제 4.2.2 펼치기

예제 4.2.2 접기 예제 4.2.2 접기

$X$와 $Y$가 독립이면 상관계수는 0이된다.

하지만 상관계수가 0이라고 $X$와 $Y$가 독립인것은 아니다.

아래 예로 확인해보자

예제 4.2.3 펼치기

예제 4.2.3 접기 예제 4.2.3 접기

연습문제 펼치기

연습문제 접기 연습문제 접기

피어슨 상관 계수 (Pearson Correlation Coefficient)

상관계수(correlation coefficient)란 두 변수가 어떤 상관 관계를 가지는가?를 의미하는 수치다.

+1은 완벽한 양의 선형 상관 관계, 0은 선형 상관 관계 없음, -1은 완벽한 음의 선형 상관 관계를 의미한다.

https://otexts.com/fppkr/graphics-scatterplots.html

X와 Y 사이의 피어슨 상관 계수를 구하는 식은 다음과 같다

\\[r_{XY} = \frac{ \sum^n_i (X_i – \bar{X})(Y_i – \bar{Y}) }{ \sqrt{\sum^n_i (X_i – \bar{X})^2} \sqrt{\sum^n_i (Y_i – \bar{Y})^2} } \\]
여기서 X, Y는 vector인데

식을 조금 들여다보면 결국 다음과 같은 과정이다.

1. 각 vector의 표본평균\$\bar{A}\$를 구해서 A의 0이 아닌 각 원소에 빼주어 normalization하고,

2. normalized 된 vector들 사이의 cosine similarity를 계산한다.

피어슨 상관 계수는 다양한 상황에서 쓰이지만,

normalized된 cosine similarity를 계산하는 것이기 때문에 피어슨 상관 계수를 similarity로도 해석할 수 있다.

피어슨 상관 계수가 similarity로 쓰이는 예로는 추천 시스템이 있다.

추천 시스템에서 collaborative filtering 방식을 사용할 때는 User-user 간, 또는 Item-item 간 similarity를 계산해야 한다.

이 때 피어슨 상관 계수를 similarity로 사용하게 된다.

유저 A와 비슷하게 영화를 평가한 유저를 찾기 위해서 user A와 나머지 유저들의 similarity를 계산하려고 한다.

movie 1 m2 m3 m4 m5 m6 m7 user A 4 5 1 user B 5 5 4 …

( 평가하지 않은 항목은 0으로 집계되기 때문에 cosine similarity를 사용하게 되면 미평가 항목이 곧 안좋게 평가한 항목과 동일하게 간주된다는 문제가 있어 피어슨 상관 계수를 사용한다.)

피어슨 상관 계수를 계산해보면

\$\bar{A} = \frac{4+5+1}{3} = \frac{10}{3} \$ \$\bar{B} = \frac{14}{3} \$

\$A – \bar{A} = [\frac{2}{3}, 0, 0, \frac{5}{3}, -\frac{7}{3}, 0, 0]\$

\$B – \bar{B} = [\frac{1}{3}, \frac{1}{3}, -\frac{2}{3}, 0, 0, 0, 0]\$

이제 이 둘의 cosine similarity를 계산하면 피어슨 상관 계수가 되고, 이는 곧 sim(A, B)가 된다.

\$sim(A, B) = 0.092\$

상관계수를 구할 때 주의할 점

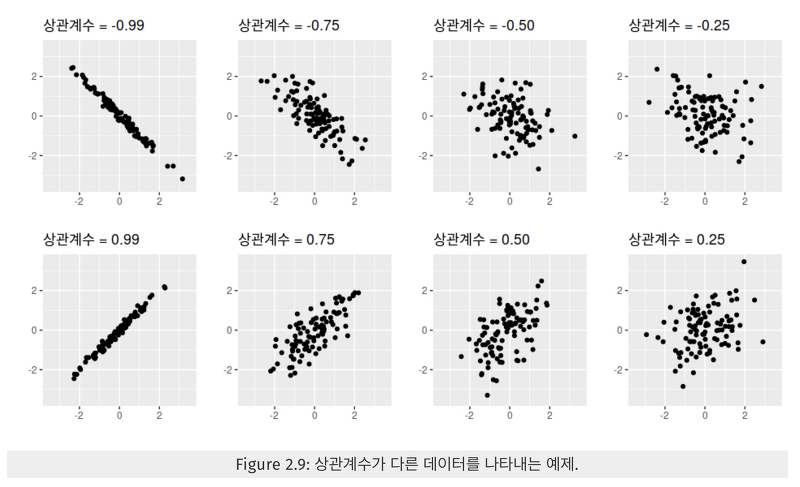
상관계수(correlation coefficient)는 선형관계의 강도만 측정하기에, 종종 오해로 이어질 수 있습니다.

아래 그래프는 모두 0.82의 상관계수를 갖습니다만, 나타나는 관계는 아주 다릅니다. 이를 통해 상관계수값에만 의존하지 말고 데이터를 그려서 살펴보는 것이 얼마나 중요한지 알 수 있습니다.

https://otexts.com/fppkr/graphics-scatterplots.html

So you have finished reading the 피어슨 상관계수 공식 topic article, if you find this article useful, please share it. Thank you very much. See more: 피어슨 상관계수 해석, 피어슨 상관계수 예시, 상관계수 계산기, 상관계수 해석 기준, correlation 상관계수, 상관계수 p값 계산, 피어슨 상관관계 분석, 스피어만 상관계수 공식

Top 32 피어슨 상관계수 공식 22766 Votes This Answer

ìê´ì ëí ë°©ë² ë° ê³µì – Minitab

피어슨 상관 계수 – 위키백과, 우리 모두의 백과사전

피어슨 상관 계수(Pearson Correlation Coefficient)

4. 상관계수 정리

피어슨 상관 계수 (Pearson Correlation Coefficient)

SPSS 피어슨 상관 계수 Pearson Correlation Coefficient, PCC : 네이버 블로그

피어슨 상관 관계 찾기 | Tableau Software

Pearson 상관 계수를 계산하는 방법

Pearson 상관계수, Spearman 상관계수, Kendall 상관계수란?

피어슨 상관 계수

피어슨 상관 계수(Pearson Correlation Coefficient)

피어슨 상관 계수 (Pearson Correlation Coefficient)

Leave a Comment Cancel reply

ìê´ì ëí ë°©ë² ë° ê³µì – Minitab

피어슨 상관 계수 – 위키백과, 우리 모두의 백과사전

피어슨 상관 계수(Pearson Correlation Coefficient)

4. 상관계수 정리

피어슨 상관 계수 (Pearson Correlation Coefficient)

SPSS 피어슨 상관 계수 Pearson Correlation Coefficient, PCC : 네이버 블로그

피어슨 상관 관계 찾기 | Tableau Software

Pearson 상관 계수를 계산하는 방법

Pearson 상관계수, Spearman 상관계수, Kendall 상관계수란?

피어슨 상관 계수

피어슨 상관 계수(Pearson Correlation Coefficient)

피어슨 상관 계수 (Pearson Correlation Coefficient)

Leave a Comment Cancel reply

ìê´ì ëí ë°©ë² ë° ê³µì – Minitab