You are looking for information, articles, knowledge about the topic nail salons open on sunday near me 법선 벡터 구하기 on Google, you do not find the information you need! Here are the best content compiled and compiled by the Chewathai27.com/to team, along with other related topics such as: 법선 벡터 구하기 방향벡터로 법선벡터 구하기, 평면에 수직인 벡터 구하기, 단위법선벡터 구하기, 법선벡터 내적, 법선벡터 직선의 방정식, 평면의 법선벡터, Normal vector 구하기, 평면의 방정식 법선벡터 구하기
세점으로 만들어지는 평면에 법선벡터 구하기(외적 구하기)
- Article author: secrys.tistory.com
- Reviews from users: 16216
Ratings
- Top rated: 4.6
- Lowest rated: 1
- Summary of article content: Articles about 세점으로 만들어지는 평면에 법선벡터 구하기(외적 구하기) 세점으로 만들어지는 평면에 법선벡터 구하기(외적 구하기). 모리노아 2009. 3. 17. 01:48 … 벡터 PQ 와 벡터 PR 에 공통으로 수직한 벡터입니다. …
- Most searched keywords: Whether you are looking for 세점으로 만들어지는 평면에 법선벡터 구하기(외적 구하기) 세점으로 만들어지는 평면에 법선벡터 구하기(외적 구하기). 모리노아 2009. 3. 17. 01:48 … 벡터 PQ 와 벡터 PR 에 공통으로 수직한 벡터입니다. p(0,0,0), Q(2,4,6), R(-1,2,7) 이 세점으로 만들어지는 평면에 법선벡터 구하기. P(0,0,0), Q(2,4,6), R(-1,2,7)에서 평면 PQR 의 법선벡터는 벡터 PQ 와 벡터 PR 에 공통으로 수직한 벡터입니다. 따라서 벡터 PQ..
- Table of Contents:
‘ETC’ Related Articles
티스토리툴바
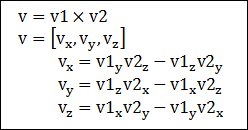
벡터 외적(Cross product)::::수학과 사는 이야기
- Article author: suhak.tistory.com
- Reviews from users: 24946
Ratings
- Top rated: 4.2
- Lowest rated: 1
- Summary of article content: Articles about 벡터 외적(Cross product)::::수학과 사는 이야기 법선벡터를 구하는 과정을 공식으로 만들어 보자. 벡터 →n … …
- Most searched keywords: Whether you are looking for 벡터 외적(Cross product)::::수학과 사는 이야기 법선벡터를 구하는 과정을 공식으로 만들어 보자. 벡터 →n … 공간도형에서 평면 방정식은 법선벡터를 구해야 알 수 있다. 다르게 표현하면 평면 위에 있는 두 벡터에 동시에 수직인 벡터를 구해야 한다. 공간에 있는 세 점 $A(1,2,-1), B(-2,1,3), C(-1,0,1)$을 지나는 평면..고등학교 수학, 미적분학, calculus, 면접, HTML, CSS, tistoryskin, Mathmatics, 여행, 사진, 야생화, 수학, 스킨
- Table of Contents:
벡터 외적(Cross product)
티스토리툴바
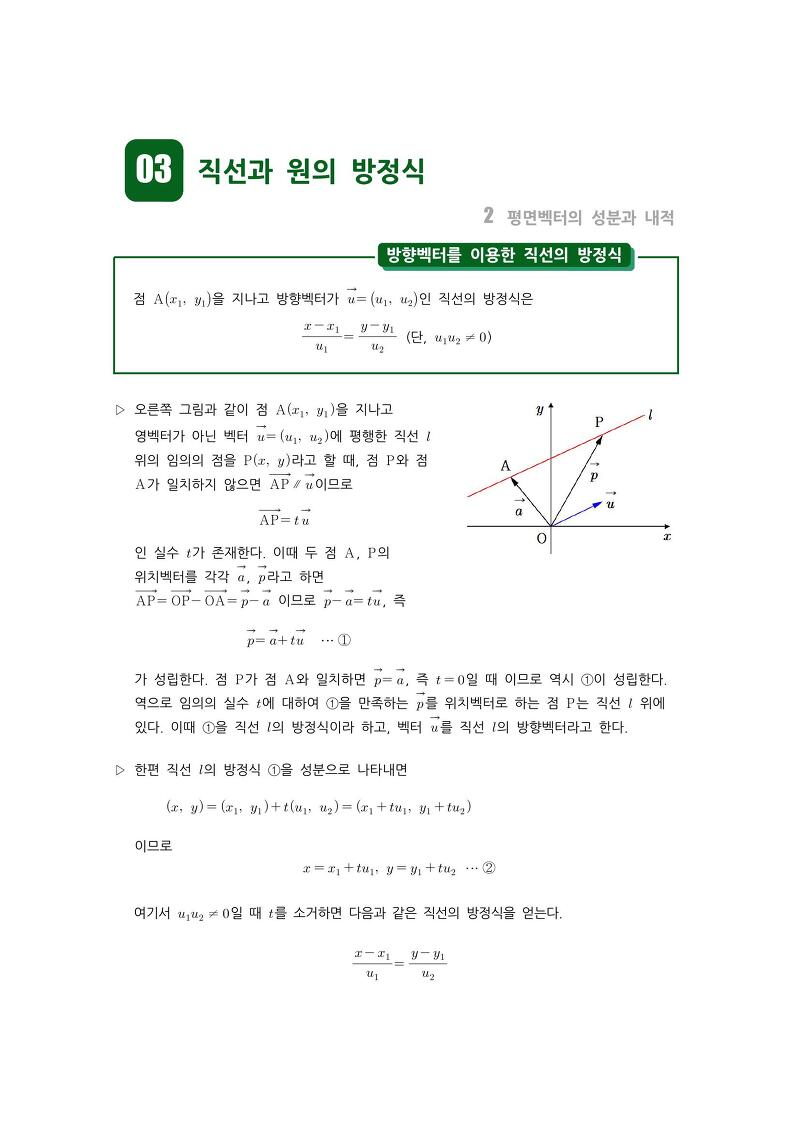
수학 개념 정리/공식 : 방향벡터를 이용한 직선의 방정식, 법선벡터를 이용한 직선의 방정식, 두 직선이 이루는 각의 크기, 벡터를 이용한 원의 방정식
- Article author: koreanfoodie.me
- Reviews from users: 41144
Ratings
- Top rated: 4.7
- Lowest rated: 1
- Summary of article content: Articles about 수학 개념 정리/공식 : 방향벡터를 이용한 직선의 방정식, 법선벡터를 이용한 직선의 방정식, 두 직선이 이루는 각의 크기, 벡터를 이용한 원의 방정식 수학 개념 정리/공식 : 방향벡터를 이용한 직선의 방정식, 법선벡터를 이용한 직선의 방정식, 두 직선이 이루는 각의 크기, 벡터를 이용한 원의 … …
- Most searched keywords: Whether you are looking for 수학 개념 정리/공식 : 방향벡터를 이용한 직선의 방정식, 법선벡터를 이용한 직선의 방정식, 두 직선이 이루는 각의 크기, 벡터를 이용한 원의 방정식 수학 개념 정리/공식 : 방향벡터를 이용한 직선의 방정식, 법선벡터를 이용한 직선의 방정식, 두 직선이 이루는 각의 크기, 벡터를 이용한 원의 …
- Table of Contents:
KoreanFoodie’s Study
수학 개념 정리공식 방향벡터를 이용한 직선의 방정식 법선벡터를 이용한 직선의 방정식 두 직선이 이루는 각의 크기 벡터를 이용한 원의 방정식 본문
http://Hybridego.net/ :: 법선 벡터 구하기
- Article author: hybridego.net
- Reviews from users: 28314
Ratings
- Top rated: 4.7
- Lowest rated: 1
- Summary of article content: Articles about http://Hybridego.net/
:: 법선 벡터 구하기 이 세점으로 만들어지는 평면에 법선벡터 구하기. P(0,0,0), Q(2,4,6), R(-1,2,7)에서 평면 PQR 의 법선벡터는 벡터 PQ 와 벡터 PR 에 공통으로 수직 … … - Most searched keywords: Whether you are looking for http://Hybridego.net/
:: 법선 벡터 구하기 이 세점으로 만들어지는 평면에 법선벡터 구하기. P(0,0,0), Q(2,4,6), R(-1,2,7)에서 평면 PQR 의 법선벡터는 벡터 PQ 와 벡터 PR 에 공통으로 수직 … 참고자료 1) p(0,0,0), Q(2,4,6), R(-1,2,7) 이 세점으로 만들어지는 평면에 법선벡터 구하기. P(0,0,0), Q(2,4,6), R(-1,2,7)에서 평면 PQR 의 법선벡터는 벡터 PQ 와 벡터 PR 에 공통으로 수직한 벡터입니다. 따.. - Table of Contents:
 Read More
Read More
[miniRT] #6 법선 구현
- Article author: velog.io
- Reviews from users: 4772
Ratings
- Top rated: 3.2
- Lowest rated: 1
- Summary of article content: Articles about [miniRT] #6 법선 구현 원점에 대해 알고 있지만 단위 백터와 길이에 대해서는 우린 알지 못한다. 단위 벡터 구하기. 단위 백터를 구하는 수식은 다음과 같다. U … …
- Most searched keywords: Whether you are looking for [miniRT] #6 법선 구현 원점에 대해 알고 있지만 단위 백터와 길이에 대해서는 우린 알지 못한다. 단위 벡터 구하기. 단위 백터를 구하는 수식은 다음과 같다. U … [miniRT] #6 법선 구현
- Table of Contents:
백터의 크기
코드로 구현한 벡터 정규화
내적(난반사) 구하기
외적(정반사) 구하기
![[miniRT] #6 법선 구현](https://velog.velcdn.com/images/sham/post/ddab629d-bfb7-44bf-af02-f8c2e4295d5c/2.png)
See more articles in the same category here: Top 423 tips update new.
세점으로 만들어지는 평면에 법선벡터 구하기(외적 구하기)
p(0,0,0), Q(2,4,6), R(-1,2,7)
이 세점으로 만들어지는 평면에 법선벡터 구하기.
P(0,0,0), Q(2,4,6), R(-1,2,7)에서 평면 PQR 의 법선벡터는
벡터 PQ 와 벡터 PR 에 공통으로 수직한 벡터입니다.
따라서 벡터 PQ와 벡터 PR 의 외적(크로스곱)을 구하면 됩니다.
벡터 PQ = Q – P = (2,4,6) – (0,0,0) = (2,4,6)
벡터 PR = R – P = (-1,2,7) – (0,0,0) = (-1,2,7)
(벡터 PQ) × (벡터 PR)
= (2,4,6) × (-1,2,7)
= (4 * 7 – 6 * 2)i – {2 * 7 – 6 * (-1)}j + {2 * 2 – 4 * (-1)}k
= 16i – 20j + 8k
= (16, -20, 8)
따라서 주어진 평면에 법선벡터는 (16, -20, 8) 입니다. 간단히 나타내려면 4를 나누어
(4, -5, 2) 라고 해도 무방합니다. (벡터의 실수배는 평행한 벡터이므로)
외적 구하는 법
반응형
벡터 외적(Cross product)
반응형
공간도형에서 평면 방정식은 법선벡터를 구해야 알 수 있다. 다르게 표현하면 평면 위에 있는 두 벡터에 동시에 수직인 벡터를 구해야 한다. 공간에 있는 세 점 $A(1,2,-1), B(-2,1,3), C(-1,0,1)$을 지나는 평면 방정식을 구해 보자.
법선벡터를 $\vec{n}=(a,b,c)$라고 하자. $\overrightarrow{AB}=(-3,-1,4),\;\;\overrightarrow{AC}=(-2,-2,2)$이고
$$\vec{n}\bot\overrightarrow{AB},\;\;\vec{n}\bot\overrightarrow{AC}$$
이므로 $$-3a-b+4c=0,\;\;-a-b+c=0$$
$2a-3c=0$에서 $\displaystyle{\frac{a}{3}=-\frac{c}{2}}$이므로 $a=5t,\;\;c=-t$이다. $b=-t$이므로 $\vec{n}=(3,-1,2)t$이다.
그러므로 평면 위의 점을 $X(x,y,z)$라고 하면 $\vec{n}\cdot\overrightarrow{AX}=0$에서
$$(3,-1,2)\cdot(x-1,y-2,z+1)=0$$
$$3x-y+2z+1=0$$
법선벡터를 구하는 과정을 공식으로 만들어 보자.
벡터 $\vec{n}=(x,y,z)$가 두 벡터 $\vec{a}=(a_1,a_2,a_3),\;\;\vec{b}=(b_1,b_2,b_3)$와 동시에 수직이라고 하자.
$$a_1x+a_2y+a_3z=0\;\;b_1x+b_2y+b_3z=0$$
$$x=(a_2 b_3-a_1 b_2)t,\;\;y=-(a_1 b_3-a_3 b_1)t,\;\;z=(a_1 b_2-a_2 b_1)t$$
임을 쉽게 확인할 수 있다. $(x,y,z)=(a_2 b_3-a_1 b_2, -a_1 b_3+a_3 b_1,a_1 b_2-a_2 b_1)$라고 할 수 있다. 이것을 외우기 쉽게 행렬식으로 정리하면 다음과 같다.
$$\Bigg(\begin{vmatrix}a_2 & a_3\\ b_2 & b_3\end{vmatrix},\;\;-\begin{vmatrix} a_1 & a_3 \\ b_1 & b_3\end{vmatrix},\;\;\begin{vmatrix}a_1 & a_2 \\ b_1 & b_2\end{vmatrix}\Bigg)$$
고등학교 교육과정엔 없지만 과학고 심화수학 책에는 나오는 벡터 외적에 대해 정리해 둔다. 위에서 적은 벡터를 기본벡터를 써서 표현하면 아래와 같다.
$$\begin{vmatrix}a_2 & a_3\\ b_2 & b_3\end{vmatrix}\vec{e_1}-\begin{vmatrix} a_1 & a_3 \\ b_1 & b_3\end{vmatrix}\vec{e_2}+\begin{vmatrix}a_1 & a_2 \\ b_1 & b_2\end{vmatrix}\vec{e_3}=\begin{vmatrix}\vec{e_1}&\vec{e_2}&\vec{e_3}\\a_1&a_2&a_3\\b_1&b_2&b_3\end{vmatrix}$$
참고 3차 행렬의 행렬식
이 벡터를 $\vec{a},\vec{b}$의 외적(cross product)이라 하고 기호로 $$\vec{a}\times\vec{b}$$로 쓴다. 두 벡터가 이루는 각을 $\theta$라고 하면 외적벡터 크기는
$$|\vec{a}\times\vec{b}|=|\vec{a}||\vec{b}|\sin\theta$$
이고 방향은 오른손 법칙을 따른다. 정리하면 두 벡터 $\vec{a},\vec{b}$에 수직인 단위벡터를 $\vec{n}$이라고 할 때,
$$\vec{a}\times\vec{b}=(|\vec{a}||\vec{b}|\sin\theta)\vec{n}$$
이다. 외적은 3차원 공간벡터에서만 정의되는 특별한 연산이다. 외적벡터는 두 벡터에 수직이고 두 벡터로 결정되는 평행사변형 넓이가 크기인 벡터이다.
외적의 성질 1) $\vec{a}\times\vec{b}=-\vec{b}\times\vec{a}$ 2) $\big(k\vec{a}\big)\times\vec{b}=k\big(\vec{a}\times\vec{b}\big)=\vec{a}\times\big(k\vec{b}\big)$ 3) $\vec{a}\times\big(\vec{b}+\vec{c}\big)=\vec{a}\times\vec{b}+\vec{a}\times\vec{c}$ 4) $\big(\vec{a}+\vec{b}\big)\times\vec{a}=\vec{b}\times\vec{a}+\vec{c}\times\vec{a}$
기본벡터를 $\vec{i},\vec{j},\vec{k}$로 표현한다면 $$\vec{ i}\times \vec{i}=\vec{ j}\times \vec{j}=\vec{ k}\times \vec{k}=\vec{0}$$와 $$\vec{i}\times \vec{j}=-\vec{j}\times\vec{ i}=\vec{k},\;\;\; \vec{j}\times \vec{k}=-\vec{k}\times \vec{j}=\vec{i},\;\;\; \vec{k}\times \vec{i}=-\vec{i}\times \vec{k}=\vec{j}$$임을 활용하여 쉽게 계산할 수 있다.
한편 세 점을 꼭짓점으로 하는 삼각형 $ABC$의 넓이 $S$는
$$S=\frac{1}{2}|\overrightarrow{AB}\times\overrightarrow{AC}|$$와 같이 쉽게 구할 수 있다.
문제 세 점 $A(1,2,-1), B(-2,1,3), C(-1,0,1)$이 주어졌을 때 삼각형 $ABC$의 넓이를 구하여라.
학원에서 아주 흔하게 가르치는 이른바 사선공식도 쉽게 보일 수 있다.
세 점 $A(a_1,a_2,0), B(b_1,b_2,0), C(c_1,c_2,0)$를 꼭짓점으로 하는 삼각형의 넓이 $S$는
$$S=\frac{1}{2}|\overrightarrow{AB}\times\overrightarrow{AC}|=\frac{1}{2}| (b_1-a_1,b_2-a_2,0)\times(c_1-a_1,c_2-a_2,0) |$$
$$=\frac{1}{2}|(b_1-a_1)(c_2-a_2)- (b_2-a_2)(c_1-a_1) |$$
$$=\frac{1}{2}|b_1a_2+c_1b_2+a_1c_2-(a_1b_2+b_1c_2+c_1a_2) |$$
외우기 쉽게 그림처럼 곱해서 차를 구한다고 가르친다. 그림을 보고 신발끈 공식으로 부르기도 한다. 모르는 이에게 신기해 보이는 공식이지만 알고 보면 별 것이 없다. 이런 걸 외우기 보다 차근차근 계산하는 것이 훨씬 좋다고 생각한다. 차라리 개념 정리를 하나 더 하는 것이 수학 공부에 도움이 될 것이다.
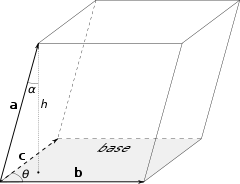
아래 그림에서 $\vec{a},\vec{b},\vec{c}$을 세 모서리로 하는 부피를 $V$라고 하자.
$$V=h |\vec{b} \times \vec{c}|=|\vec{a}| \cos \alpha | \vec{b} \times \vec{c} |= \vec{a}\cdot(\vec{b}\times \vec{c})$$
반응형
http://Hybridego.net/
분류 전체보기 (2146) SeeFar (74) 世上事 (41) Books (3) 외국어 (45) 영어 (43) 일어 (1) 영상편집 (13) 사진기술 (4) 서버관련지식 (2) 삶의 지혜 (46) 컴, 하드웨어, IT (143) Wireless Tech. (41) 잡것들 (42) 취업 (5) 경제관련 (40) 디스플레이 (9) Tip & Tech. (70) 자료구조 & 알고리즘 (15) C & C++ 관련 (111) Computer_Graphics (35) .Net (28) SilverLight (4) Windows CE & Mobile (6) Linux (373) Linux 일반 (140) Linux 명령어 (40) Linux Kernel (78) Shell Script (11) GamePrograming (22) NDSL (6) Panda3D (3) DirectX (1) DB (26) My SQL (10) Oracle (2) CUBRID (0) JDBC (6) GamePlatform관련 (3) git (10) Python (75) JAVA (34) WIPI (1) Ruby on Rails (2) D 언어 (1) JSP (5) Android (428) NDK (14) Embeded (159) ROS (13) WindowsPrograming (32) 멀티미디어 (77) Network (32) WebPrograming관련 (51) Adobe Flex (8) Programing 미분류 (39) golang (1) 안드로이드의 모든 것 NDK (2)
So you have finished reading the 법선 벡터 구하기 topic article, if you find this article useful, please share it. Thank you very much. See more: 방향벡터로 법선벡터 구하기, 평면에 수직인 벡터 구하기, 단위법선벡터 구하기, 법선벡터 내적, 법선벡터 직선의 방정식, 평면의 법선벡터, Normal vector 구하기, 평면의 방정식 법선벡터 구하기

