You are looking for information, articles, knowledge about the topic nail salons open on sunday near me 마르코프 연쇄 몬테카를로 방법 on Google, you do not find the information you need! Here are the best content compiled and compiled by the Chewathai27.com/to team, along with other related topics such as: 마르코프 연쇄 몬테카를로 방법 마르코프 연쇄 설명, 마르코프 체인, MCMC 알고리즘, 쉽게 쓰여진 MCMC, 몬테카를로 시뮬레이션 확률분포, 마르코프 가정, Metropolis-Hastings 알고리즘, MCMC 수렴
마르코프 연쇄 몬테카를로 방법(무작위 행보 몬테 카를로 방법 포함)은 마르코프 연쇄의 구성에 기반한 확률 분포로부터 원하는 분포의 정적 분포를 갖는 표본을 추출하는 알고리즘의 한 부류이다.
마르코프 연쇄 몬테카를로 – 위키백과, 우리 모두의 백과사전
- Article author: ko.wikipedia.org
- Reviews from users: 35089
Ratings
- Top rated: 4.2
- Lowest rated: 1
- Summary of article content: Articles about 마르코프 연쇄 몬테카를로 – 위키백과, 우리 모두의 백과사전 Updating …
- Most searched keywords: Whether you are looking for 마르코프 연쇄 몬테카를로 – 위키백과, 우리 모두의 백과사전 Updating
- Table of Contents:
무작위 행보 알고리즘 (Random walk algorithm)[편집]
무작위 행보를 피하기[편집]
같이 보기[편집]
출처참고[편집]

Markov Chain Monte Carlo – 공돌이의 수학정리노트
- Article author: angeloyeo.github.io
- Reviews from users: 29430
Ratings
- Top rated: 4.9
- Lowest rated: 1
- Summary of article content: Articles about Markov Chain Monte Carlo – 공돌이의 수학정리노트 위키피디아에 따르면 마르코프 연쇄 몬테카를로 방법(Markov Chain Monte Carlo, MCMC)은 “마르코프 연쇄의 구성에 기반한 확률 분포로부터 원하는 … …
- Most searched keywords: Whether you are looking for Markov Chain Monte Carlo – 공돌이의 수학정리노트 위키피디아에 따르면 마르코프 연쇄 몬테카를로 방법(Markov Chain Monte Carlo, MCMC)은 “마르코프 연쇄의 구성에 기반한 확률 분포로부터 원하는 … Interactive MCMC JS Applet by Chi-Feng, 소스코드 prerequisites이 포스팅에 대해 잘 이해하기 위해선 다음의 내용에 대해 알고 오시는 것이 좋습니다. Rejection Sampling likelihood의 의미MCMC의 정의위키피디아에 따…
- Table of Contents:
샘플링 과정 (Metropolis 알고리즘)
알고리즘의 pseudo-code
제안 분포가 symmetric 하지 않은 경우는
샘플링 결과
prerequisites
주어진 것은 무엇인가
추정 과정
추정의 결과

마르코프 연쇄 몬테카를로 방법
- Article author: bryan7.tistory.com
- Reviews from users: 39484
Ratings
- Top rated: 5.0
- Lowest rated: 1
- Summary of article content: Articles about 마르코프 연쇄 몬테카를로 방법 MCMC 방법이란 다변량 분포에서 표본을 근사적으로 추출하는 여러 가지. 반복적인 방법들을 통틀어 일컫는 말이다. 그러면, 이러한 몇 가지 방법론. 과 그 기본 성질들을 … …
- Most searched keywords: Whether you are looking for 마르코프 연쇄 몬테카를로 방법 MCMC 방법이란 다변량 분포에서 표본을 근사적으로 추출하는 여러 가지. 반복적인 방법들을 통틀어 일컫는 말이다. 그러면, 이러한 몇 가지 방법론. 과 그 기본 성질들을 …
- Table of Contents:

마르코프 연쇄 몬테카를로 방법
- Article author: www.koreascience.or.kr
- Reviews from users: 15420
Ratings
- Top rated: 4.3
- Lowest rated: 1
- Summary of article content: Articles about 마르코프 연쇄 몬테카를로 방법 특히 확률변수의 샘플. 링에 있어서 마르코프 연쇄 몬테 카를로(Markov chain. Monte Carlo, MCMC) 방법을 이용하여 효율성을 높일. 수 있도록 한다. 개발한 해석 모델을 … …
- Most searched keywords: Whether you are looking for 마르코프 연쇄 몬테카를로 방법 특히 확률변수의 샘플. 링에 있어서 마르코프 연쇄 몬테 카를로(Markov chain. Monte Carlo, MCMC) 방법을 이용하여 효율성을 높일. 수 있도록 한다. 개발한 해석 모델을 …
- Table of Contents:

24. Markov chain Monte Carlo (MCMC) inference – Knowledge Dictionary
- Article author: frozenca.wordpress.com
- Reviews from users: 44871
Ratings
- Top rated: 3.2
- Lowest rated: 1
- Summary of article content: Articles about 24. Markov chain Monte Carlo (MCMC) inference – Knowledge Dictionary 마르코프 연쇄 몬테 카를로(MCMC) : 고차원 분포에서 샘플링하는 가장 널리 쓰이는 방법으로, 목표하는 확률분포를 정지 분포로 갖는 마르코프 연쇄를 … …
- Most searched keywords: Whether you are looking for 24. Markov chain Monte Carlo (MCMC) inference – Knowledge Dictionary 마르코프 연쇄 몬테 카를로(MCMC) : 고차원 분포에서 샘플링하는 가장 널리 쓰이는 방법으로, 목표하는 확률분포를 정지 분포로 갖는 마르코프 연쇄를 … 24.1. Introduction 앞 장에서 배웠던 몬테 카를로 법은 고차원에 대해 잘 작동하지 않는다는 점이었다. 고차원 분포에서 샘플링하는 가장 널리 쓰이는 방법은 마르코프 연쇄 몬테 카를로(MCMC)이다. MCMC의 기본 아이디어는 목표하는 확률분포를 정지 분포로 갖는 마르코프 연쇄를 만든 뒤 상태 공간에서 무작위 걸음을 해서 각 상태 $latex \mathbf{x}$에서 소비하는 시간이 $latex p^{\ast}(\mathbf{x})&s=1$에 비례하도록 하는 것이다. 이 연쇄로부터…
- Table of Contents:
검색
사이드바 텍스트 위젯
글 네비게이션
마르코프 연쇄 몬테카를로 방법 – 수학노트
- Article author: wiki.mathnt.net
- Reviews from users: 46055
Ratings
- Top rated: 3.7
- Lowest rated: 1
- Summary of article content: Articles about 마르코프 연쇄 몬테카를로 방법 – 수학노트 마르코프 연쇄 몬테카를로 방법 … Strict detailed balance is not necessary for Markov chain Monte Carlo simulations to converge to the correct equilibrium … …
- Most searched keywords: Whether you are looking for 마르코프 연쇄 몬테카를로 방법 – 수학노트 마르코프 연쇄 몬테카를로 방법 … Strict detailed balance is not necessary for Markov chain Monte Carlo simulations to converge to the correct equilibrium …
- Table of Contents:
목차
노트
메타데이터
둘러보기 메뉴

마르코프 연쇄 몬테카를로 방법
- Article author: ko.dbpedia.org
- Reviews from users: 33061
Ratings
- Top rated: 3.9
- Lowest rated: 1
- Summary of article content: Articles about 마르코프 연쇄 몬테카를로 방법 마르코프 연쇄 몬테카를로 방법(무작위 행보 몬테 카를로 방법 포함)은 마르코프 연쇄의 구성에 기반한 확률 분포로부터 원하는 분포의 정적 분포를 갖는 표본을 추출 … …
- Most searched keywords: Whether you are looking for 마르코프 연쇄 몬테카를로 방법 마르코프 연쇄 몬테카를로 방법(무작위 행보 몬테 카를로 방법 포함)은 마르코프 연쇄의 구성에 기반한 확률 분포로부터 원하는 분포의 정적 분포를 갖는 표본을 추출 …
- Table of Contents:

See more articles in the same category here: Top 423 tips update new.
마르코프 연쇄 몬테카를로
마르코프 연쇄 몬테카를로 방법(무작위 행보 몬테 카를로 방법 포함)은 마르코프 연쇄의 구성에 기반한 확률 분포로부터 원하는 분포의 정적 분포를 갖는 표본을 추출하는 알고리즘의 한 부류이다. 큰 수의 단계(step) 이후에 연쇄의 상태는 목표로 하는 분포로부터 추출된 표본처럼 사용될 수 있다. 표본의 품질은 단계 수의 함수로 개선된다. 일반적으로 원하는 특성을 갖는 마르코프 연쇄를 구성하는 것은 어렵지 않다. 보다 어려운 문제는 수용할 만한 오차 범위의 정적 분포로 수렴하는데까지 얼마나 많은 단계가 필요한지를 결정하는 것이다. 좋은 연쇄는 임의의 위치에서부터 시작하여 정적 분포에 빠르게 도달하는 빠른 혼합(mixing)을 가질 것이며, 이에 대해서는 마르코프 연쇄 혼합 시간에서 상세히 설명된다.
MCMC의 전형적인 사용은 목표 분포를 근사하는 것이며, 여기에는 항상 시작 위치로부터의 약간의 잔여 효과(residual effect)가 존재한다.
이 알고리즘의 가장 일반적인 적용 예는 다차원 적분을 수치적으로 계산하는 것이다.
무작위 행보 알고리즘 (Random walk algorithm) [ 편집 ]
많은 MCMC 방법은 평형 분포(equilibrium distribution) 주위에서 비교적 작은 보폭으로 움직이며, 이 보폭은 동일한 방향으로 진행하려는 경향을 갖지 않는다. 이 방법은 구현하기로 쉽고 분석하기도 쉽지만, 보행자(walker)가 모든 공간을 탐색하는데에는 오랜 시간이 걸린다. 보행자는 종종 왔다갔다 하기도 하고 갔던 곳을 다시 가기도 한다. 다음은 몇가지 무작위 행보 MCMC 방법들이다.
메트로폴리스 해스팅스 알고리즘: 제안된 밀도와 제안된 이동을 거부하는 방법을 이용하여 무작위 행보를 생성한다.
깁스 표집: 목표 분포의 모든 조건 분포가 정확하게 추출되는 것을 필요로 한다. 이 방법은 어떠한 튜닝도 필요하지 않다는 점 때문에 인기가 있다.
무작위 행보를 피하기 [ 편집 ]
좀 더 복잡한 알고리즘은 보행자가 왔다 갔다 하는 것을 방지하기 위해 몇가지 방법을 사용한다. 이러한 알고리즘은 구현하기가 더 어려울 수 있지만, 보다 빠른 수렴을 보여주기도 한다.
Successive over-relaxation : 이 방법은 깁스 샘플링(Gibbs sampling)의 변형이며, 종종 무작위 행보를 피한다.
하이브리드 몬테 카를로 (HMC) (‘해밀토니언 몬테 카를로’라고 불림) : 부가적인 모멘텀 벡터를 도입하고 목표 밀도의 포텐션 함수를 갖는 해밀토니언 역학을 구현하여 무작위 행보를 피하려고 한다.
같이 보기 [ 편집 ]
Markov Chain Monte Carlo
Interactive MCMC JS Applet by Chi-Feng, 소스코드
prerequisites
이 포스팅에 대해 잘 이해하기 위해선 다음의 내용에 대해 알고 오시는 것이 좋습니다.
MCMC의 정의
위키피디아에 따르면 마르코프 연쇄 몬테카를로 방법(Markov Chain Monte Carlo, MCMC)은 “마르코프 연쇄의 구성에 기반한 확률 분포로부터 원하는 분포의 정적 분포를 갖는 표본을 추출하는 알고리즘의 한 분류이다.”라고 나와있다.
복잡해보이지만 우선 MCMC는 샘플링 방법 중 하나인 것이라는 것만 알고있도록 하자. 언제나 그렇듯 정의만 보면 처음 볼 때는 이해할 수 있는 것이 거의 없기에 하나 하나 뜯어서 살펴볼 것이다.
이번 포스팅에서는 복잡한 수학적 내용을 전달하는 것 보다는 MCMC의 의미를 이해할 수 있도록하는데 초점을 맞추고자 한다.
Monte Carlo
Monte Carlo는 쉽게 말해 통계적인 수치를 얻기 위해 수행하는 ‘시뮬레이션’ 같은 것이다.
굳이 이런 시뮬레이션을 하는 이유는 통계학의 특성 상 무한히 많은 시도를 거쳐야만 진짜 정답이 뭔지 알 수 있지만, 그렇게 하기가 현실적으로 어렵기 때문에 유한한 시도만으로 정답을 추정하자는 데 의미가 있다.
Monte Carlo 방식의 시뮬레이션 중 가장 유명한 것 중 하나가 원의 넓이를 계산하는 시뮬레이션이다.
아래의 그림과 같이 가로, 세로의 길이가 2인 정사각형 안에 점을 무수히 많이 찍으면서, 중심으로부터의 거리가 1이하면 빨간색으로 칠하고, 그렇지 않으면 파란색으로 칠해준다.
전체적으로 찍은 점의 개수와 빨간색으로 찍힌 점의 개수의 비율을 계산하여 원래의 사각형의 면적인 4를 곱해주면 반지름이 1인 원의 넓이를 대략적으로 추정할 수 있다.
그림 1. 반지름이 1인 원의 넓이를 근사적으로 계산하는 Monte Carlo 시뮬레이션
MCMC에서는 “통계적인 특성을 이용해 무수히 뭔가를 많이 시도해본다”는 의미에서 Monte Carlo라는 이름을 붙였다고 보면 좋을 것 같다.
Markov Chain
Markov Chain은 어떤 상태에서 다른 상태로 넘어갈 때, 바로 전 단계의 상태에만 영향을 받는 확률 과정을 의미한다.
이렇게 들으면 어렵게 들릴 수도 있겠지만, 다음과 같은 비유를 생각해보자.
보통 사람들은 전날 먹은 식사와 유사한 식사를 하지 않으려는 경향이 있다. 가령, 어제 짜장면을 먹었다면 오늘은 면종류의 음식을 먹으려고 하지 않는다.
이렇듯 음식 선택이라는 확률과정에 대해 오늘의 음식 선택이라는 과정은 어제의 음식 선택에만 영향을 받고, 그저께의 음식 선택에는 영향을 받지 않는다면
이 과정은 마르코프 성질(Markov property)을 가진다고 할 수 있으며, 이 확률 과정은 Markov chain이라고 할 수 있다.
앞서 MCMC는 샘플링 방법 중 하나라고 하였는데, “가장 마지막에 뽑힌 샘플이 다음번 샘플을 추천해준다”는 의미에서 Markov Chain이라는 단어가 들어갔다고 보면 좋을 것 같다.
MCMC를 이용한 샘플링
MCMC는 Monte Carlo와 Markov Chain의 개념을 합친 것이다.
다시 말해 MCMC를 수행한다는 것은 첫 샘플을 랜덤하게 선정한 뒤, 첫 샘플에 의해 그 다음번 샘플이 추천되는 방식의 시도를 무수하게 해본다는 의미를 갖고 있다.
위의 문장에서 가장 수학적이지 않은 단어는 뭘까? 바로 “추천”이다.
또, 추천 다음에는 “승낙/거절”의 단계까지도 포함되는데, 이 과정에 대해 알아보도록 하자.
참고로 이 post에서 주요하게 소개하는 MCMC 샘플링 알고리즘은 Metropolis 알고리즘이다.
샘플링 과정 (Metropolis 알고리즘)
우선은 Rejection Sampling을 할 때와 마찬가지로 샘플을 추출하고자 하는 target 분포가 하나 있어야 한다.
이 타겟 분포는 정확히는 확률밀도 함수가 아니어도 괜찮다. 대략적으로 확률밀도 함수의 크기에 비례하는 함수를 이용하면 충분하다.
가령 아래와 같은 함수를 타겟 분포로 사용할 수 있다.
\[f(x) = 0.3\exp\left(-0.2x^2\right) + 0.7\exp\left(-0.2(x-10)^2\right)\]
이 함수는 $-\infty$부터 $\infty$까지의 전체 면적이 1이 아니기 때문에 확률밀도 함수라고 할수는 없다. 하지만, 만약 우리가 실험적인 결과로 확률밀도함수가 대략적으로 타겟 함수 $f(x)$와 비슷한 형태를 띄고 있다는 것을 알고 있다면 우리는 이러한 타겟 함수로부터 실제 확률밀도함수를 근사하기 위해 샘플링이 필요할 수 있다.
1. random initialization
MCMC의 샘플링 과정에서 가장 먼저 수행해줄 것은 random initialization이다.
쉽게 말해 샘플 공간에서 아무런 입력값이나 하나를 선택해 주는 것이다.
가령 아래의 그림과 같이 $x_0$를 임의로 선택할 수 있다.
아래 그림에서는 $x_0 = 7$로 설정해보았다.
그림 2. target 분포와는 크게 관계없이 임의의 시작 포인트를 선택하여 MCMC 알고리즘을 시작한다.
2. 제안 분포로부터 다음 포인트를 추천받기
MCMC의 그 다음번 스텝은 제안 분포로부터 다음번으로 추출해볼 샘플을 추천받는 것이다.
제안분포는 어떤 확률분포를 이용해도 상관없으나, Metropolis는 symmetric한 확률분포를 사용하는 경우에 대한 알고리즘을 제안했고, Hastings는 일반적인 확률 분포에 대한 경우까지 어떻게 수학적으로 계산할 수 있는지에 관해 Metropolis가 제안한 알고리즘을 확장하였다.
우리는 논의를 쉽게 하기 위해서 symmetric한 확률분포를 제안분포로 사용해보도록 하자.
여기서 제안분포는 $g(x)$라고 부르도록 하자.
보통 symmetric한 제안분포로 많이 사용되는 확률분포는 예상했겠지만 정규분포이다.
그러면, 처음 시작으로 잡은 $x_0$를 중심으로 정규분포를 하나 그려본다.
이 때, 정규분포의 너비(즉, 표준 편차)는 연구자의 선택에 따라 임의로 설정하면 된다.
이번 그림에서는 표준편차를 2로 설정해보았다.
그림 3. 시작점에서 제안 분포를 형성하자.
잘 생각해보면 우리의 제안 분포는 정규분포인데 평균이 7이고 표준편차가 2이다.
이런 정규분포에서는 샘플을 추출하기가 쉽다. MATLAB에서는 randn()함수를 이용해서 쉽게 표본을 추출할 수 있다.
아래와 같이 제안 분포로부터 다음 포인트를 추천받아보자.
그림 4. 제안분포로부터 다음 포인트를 추천 받았을 때 어떤 경우는 추천을 거절하고, 어떤 경우는 추천을 수용한다.
그림 4를 보면 파란색 점으로 표시한 것들이 새롭게 제안된 샘플 포인트와 그 포인트에서의 타겟 분포의 값을 표현하였다.
또, 그림 4를 잘 보면 왼쪽 그림에서 제안된 새로운 샘플 포인트는 거절됐고, 오른쪽 그림에서 제안된 새로운 샘플 포인트는 수용되었다.
거절의 이유는 타겟 분포에서의 높이가 원래의 $x_0$에서의 높이보다 제안된 샘플 포인트의 타겟 분포의 높이보다 낮아서이고,
수용의 이유는 반대로 타겟 분포에서의 높이가 원래의 $x_0$에서의 높이보다 제안된 샘플 포인트의 타겟 분포에서의 높이보다 높아서이다.
즉, 다음의 기준에 따라 수용 여부를 결정한다.
\[\frac{f(x_1)}{f(x_0)}>1\]
만약, 제안이 수용되었다면 수용된 샘플 포인트를 중심으로 제안 분포를 그리고 이를 통해 샘플을 또 추천받아본다.
그런데, 제안이 수용되지 않았다면 통계적으로 수용하게끔 MCMC는 패자부활전을 마련해놓았다.
3. 패자부활전
앞서 2번 단계에서 거절된 샘플들은 무조건 이용하지 않는 것은 아니고 통계적으로 수용할 수 있게 만들어놓았다.
원래의 샘플의 위치를 $x_0$라고 하고 제안 분포를 통해 새로 제안 받은 샘플의 위치를 $x_1$이라고 하자.
이 때, target 분포를 지금까지 처럼 $f(x)$라고 하면 다음에 대해 확인해본다.
uniform distribution $U_{(0,1)}$에서 부터 추출한 임의의 샘플 $u$에 대해서,
\[\frac{f(x_1)}{f(x_0)}>u\]
만약 수식 (3)이 만족되면, 이 샘플은 비록 타겟 분포에서 새로운 샘플에 대한 높이가 더 높지는 않았지만 수용하게 된다.
만약 여기서도 수식 (3)을 만족하지 못하면 그 때는 새로운 샘플 $x_1$을 샘플링하기를 수용하지 않고, $x_1$을 $x_0$으로 설정한 뒤 다음 샘플($x_2$)을 추천 받는다.
이와 같은 2~3의 단계를 계속 수행해나가면 된다.
알고리즘의 pseudo-code
여기까지가 MCMC 알고리즘의 끝이다. 정말 간단하다.
이 내용을 pseudo-code로 작성하면 다음과 같다.
Initialize $x_0$ For $i=0$ to $N-1$ Sample $u\sim U_{[0,1])}$ Sample $x_{new}~g(x_{new}|x_i))$ If $u\lt A(x_i, x_{new}) = min\left\lbrace 1, f(x_{new})/f(x_i)\right\rbrace$ $\quad x_{i+1} = x_{new}$ else $\quad x_{i+1} = x_i$
제안 분포가 symmetric 하지 않은 경우는?
위의 샘플링 과정 전체를 통틀어 제안 분포가 symmetric 하지 않은 경우에 관한 알고리즘이 Metropolis 알고리즘을 업그레이드한 Metropolis-Hastings 알고리즘이다.
Metropolis-Hastings 알고리즘에서는 수식 (2)에서 보였던 타겟 분포의 likelihood 비교 시에 제안 분포의 높이도 함께 이용해 그 값을 보정해주어야 한다.
즉, 수식 (2)의 기준은 다음과 같이 보정될 수 있다.
제안 분포를 $g(x)$라고 할 때,
\[수식(2) \Rightarrow \frac{f(x_1)/g(x_1|x_0)} {f(x_0)/g(x_0|x_1)}\]
다시 말해 수식 (4)의 분자를 보면 새로운 포인트 $x_1$에 대해서는 $x_0$를 기준으로 뽑은 $g(x_1|x_0)$ 값을 이용해 정규화 해주고,
또, 이전의 포인트 $x_0$에 대해서는 새로운 $x_1$을 기준으로 $g(x_0|x_1)$의 값을 이용해 정규화 해주었다고 볼 수 있다.
샘플링 결과
위에서 설명한 Metropolis 알고리즘을 이용해 샘플링을 하면 아래와 같은 결과를 얻을 수 있다.
그림 5. MCMC 알고리즘을 이용해 샘플링한 결과
이 결과를 얻기 위한 MATLAB 코드는 아래와 같다.
clear; close all; clc; % 참고문헌: https://www.cs.ubc.ca/~arnaud/andrieu_defreitas_doucet_jordan_intromontecarlomachinelearning.pdf % % rng(1) n_iter = 5000; target = @(x) 0.3*exp(-0.2 * x.^2) + 0.7 * exp(-0.2 * (x – 10).^2); xx = linspace(-10,20, 1000); %% Metropolis Hastings % initialize x_0 x = []; x = [x, (rand(1, 1) – 0.5) * 30 + 5]; % -10에서 20사이의 범위에서 random uniform proposal = @(x, mu, s) 1/(s*sqrt(2*pi))*exp(-(x-mu)^2/(2*s^2)); % 정규분포 my_std = 10; for i = 1 : n_iter u = rand(1); % sample u x_old = x(i); % 제안 분포 q(x_new | x_old) = N(x_old, sigma)로부터 샘플 추출 x_new = randn(1) * my_std + x_old; % A(x_old, x_new) 계산 A = min(1, … (target(x_new) * proposal(x_old, x_new, my_std)) / … (target(x_old) * proposal(x_new, x_old, my_std))… ); if u < A x = [x x_new]; else x = [x x_old]; end end %% 결과 plot figure; h = histogram(x,'BinWidth',0.5, 'Normalization','probability'); hold on; plot(xx, target(xx)/max(target(xx))*max(h.Values),'linewidth',2) grid on; xlabel('x'); MCMC를 이용한 Bayesian estimation 샘플링 뿐만 아니라 MCMC는 파라미터 추정에도 사용될 수 있다. prerequisites 이 내용에 대해 잘 이해하시려면 다음의 내용에 대해 알고 오시는 것을 추천드립니다. 주어진 것은 무엇인가? 이번에는 MCMC를 이용해 파라미터 추정을 수행해보도록 하자. 가령, 다음과 같이 평균이 10, 표준편차가 3인 정규분포를 따르는 30,000 개의 원소들로 구성된 모집단에서 1,000개의 표본을 추출할 수 있었다고 해보자. 그림 6. Bayesian estimation을 위해 준비된 1,000개의 샘플 우리가 알고싶은 것은 이 1,000개의 샘플만을 이용해서 30,000개의 전체 모집단의 평균 값을 더 잘 추정해보는 것이다. 추정 과정 1. random initialization 기본적으로 MCMC의 샘플링 과정과 동일하게 파라미터 추정 시에도 random initialization으로 MCMC 알고리즘이 시작된다. 우리가 추정하고자 하는 모집단의 확률밀도함수는 정규분포를 따른다고 알고있다고 하면, 우리는 평균과 표준편차 두 가지 파라미터에 대해 추정해볼 수 있겠다. 하지만, 여기서는 설명의 편의를 위해 평균 값에 대해서만 추정하고 표준편차는 표본 표준편차를 그대로 사용하도록 하자. 먼저, random하게 initialize하는 것이 원칙이나 평균값 1로부터 시작해서 실제로 추정값이 참값인 10에 가까워지는지 확인해보자. 위 1,000개의 샘플의 표본 표준편차는 3.1591이라고 계산할 수 있었다. 따라서 우리의 타겟분포는 가우시안 분포이며, 그 표준편차는 3.1591로 계속 고정된 채로 움직일 것이다. 2. 제안 분포를 이용해 mean 값을 제안 받기 샘플링 과정과 동일한 방식으로 MCMC에서 이용되는 알고리즘을 이용해 제안 분포를 통해 새로운 mean 값을 추천 받도록 하자. 그러기 위해 initialize 된 평균값 1을 중심으로 제안 분포를 하나 그리자. 제안 분포는 어떤 것을 사용하여도 좋지만 논의의 편의성을 위해 symmetric한 확률분포 중 하나인 정규분포를 이용하자. 제안 분포로 사용되는 정규분포는 표준편차가 0.5인 것을 이용할 것이다. 그러면 이 제안분포에서 샘플링을 통해 새로운 mean 값을 추천받을 수 있다. 그림 7. $\mu=\mu_{old}$가 중심인 제안 분포로부터 새로운 샘플을 추출해 새로운 $\mu$를 추천받을 수 있다. 3. 추천 받은 제안에 대한 수락 혹은 거절 ※ 여기서부터는 베이즈 정리가 나오고 수식이 복잡해지만, 마지막 식 (13)의 결과만 알고있어도 MCMC를 이해하는데에는 큰 무리가 없음. ※ 그럼 이제는 추천 받은 mean 값을 accept하거나 reject해야한다. accept 혹은 reject의 기준은 이전의 sampling method에서와 마찬가지로 타겟 함수의 높이 비교를 통해 이루어질 수 있다. 하지만, 약간 다른 것은 이번에는 타겟 함수의 파라미터가 변경된 두 경우를 비교하는 것이라는 점이다. 왜 파라미터가 변경된 두 경우에 대한 비교를 수행하는 것일까? 그것은 지금하고자 하는 일이 파라미터 추정이며 파라미터 추정에서는 이전 파라미터(여기서는 평균)에 비해 지금 파라미터가 더 좋은가를 확인해야하기 때문이다. 다시 말해, 아래와 같은 수식을 기준으로 비교가 이루어진다고 할 수 있다. 이 비교 기준을 만족하면 제안을 수락하고 그렇지 못하면 거절하게 된다. \[기준: \frac{f_{new}(x)}{f_{old}(x)} > 1\]
식 (5)를 다시 쓰면 다음과 같이도 쓸 수 있다.
\[\frac{P(\theta = \theta_{new}|Data)}{P(\theta = \theta_{old}|Data)}>1\]
식 (6)에서 $Data$는 그림 6에서 본 1,000개의 샘플이라고 할 수 있다.
여기서, 베이즈 정리에 따라 식 (6)을 변형시키면 다음과 같다.
\[\frac{f(D|\theta=\theta_{new})P(\theta=\theta_{new})/f(D)} {f(D|\theta=\theta_{old})P(\theta=\theta_{old})/f(D)}>1\]
식 (7)에서 $f(D)$는 분자 분모에서 동일하므로 제거하면 아래와 같다.
\[식(7) \Rightarrow \frac{f(D|\theta=\theta_{new})P(\theta=\theta_{new})} {f(D|\theta=\theta_{old})P(\theta=\theta_{old})}>1\]
분자나 분모에서 $f(D|\theta)$와 관련된 항은 모두 전체 데이터의 likelihood를 의미하는데 모든 데이터가 독립적으로 얻어졌다고 가정하면 다음과 같이 각각의 데이터에 대해 풀어쓸 수 있게 된다.
\[f(D|\theta) = \prod_{i=1}^N f(d_i|\theta)\]
여기서 전체 데이터의 개수가 $N$개이고 각각의 데이터들은 $d_i$로 표현했다.
여기서 우리의 target 분포는 정규분포이므로,
\[식(9)\Rightarrow \prod_{i=1}^{N}\frac{1}{\sigma\sqrt{2\pi}}\exp\left(-\frac{(d_i-\mu)^2}{2\sigma^2}\right)\]
계산의 편의를 위해 식 (10)에 자연로그를 취하도록 하자.
\[\Rightarrow \sum_{i=1}^{N}\left\lbrace\log\left(\frac{1}{\sigma\sqrt{2\pi}}\right)-\frac{(d_i-\mu)^2}{2\sigma^2}\right\rbrace\] \[=\sum_{i=1}^{N}\left\lbrace-\log(\sigma\sqrt{2\pi})-\frac{(d_i-\mu)^2}{2\sigma^2}\right\rbrace\]
이제 원래의 식 (8)도 마찬가지로 자연로그를 취해주고, 식 (12)를 대입해주면 아래와 같다.
\[식(8)\Rightarrow \frac{\sum_{i=1}^{N}\left\lbrace-\log(\sigma\sqrt{2\pi})-\frac{(d_i-\mu_{new})^2}{2\sigma^2}\right\rbrace + \log(P(\mu = \mu_{new}))} {\sum_{i=1}^{N}\left\lbrace-\log(\sigma\sqrt{2\pi})-\frac{(d_i-\mu_{old})^2}{2\sigma^2}\right\rbrace + \log(P(\mu = \mu_{old}))} > 1\]
그럼 식 (13)이 의미하는 바는 무엇일까?
이것은 주어진 데이터에 대해 $\mu=\mu_{old}$인 경우와 $\mu=\mu_{new}$인 경우의 likelihood $\times$ prior를 비교한 것과 같다는 것을 알 수 있다.
아래의 그림 8에서는 기존의 $\mu = \mu_{old}$인 경우와 $\mu=\mu_{new}$인 경우의 target 분포에 대해 모든 데이터로부터 likelihood 값을 얻는 과정을 보여주고 있다.
그림 8. $\mu=\mu_{old}$인 경우와 $\mu=\mu_{new}$ 인 경우에 대해 모든 데이터의 likelihood들을 곱해주는 과정
비록 그림 8에서는 5개의 데이터만 보여주었지만, $\mu=\mu_{old}$인 경우에 비해 $\mu=\mu_{new}$인 경우가 실제 모평균 값(10)과 더 가깝기 때문에 더 likelihood(확률밀도함수의 높이)가 큰 데이터들이 많고 실제로 likelihood를 모두 곱해준 뒤 prior와 곱해 비교해주면 $\mu=\mu_{new}$로 추천한 것이 채택될 수 있을 것이다.
이제, 식 (13)을 보면 $\sigma$와 $\mu_{new}$, $\mu_{old}$는 모두 주어져 있기 때문에 계산을 하는데 아무런 문제가 없지만 $P(\mu=\mu_{new})$나 $P(\mu=\mu_{old})$와 같은 prior는 어떻게 계산 해주어야 할까?
베이즈 정리의 의미편이나 Naive Bayes 분류기 편에서 보았던 것 처럼 Prior는 일종의 사전지식으로, 여기서는 굉장히 사소하더라도 $\mu$ 값에 대한 정보를 입력해주면 된다.
여기서는 그림 6을 봤을 때 대략적으로나마 알 수 있는 것 처럼 추정하고자 하는 $\mu$값은 최소한 0보다는 클것이라는 사전 지식을 이용해주자. 즉, 여기서는 prior를 아래와 같이 설정할 수 있다.
\[P(\mu) = \begin{cases}1 && \text{if }\mu\gt 0 \\ 0 && \text{otherwise}\end{cases}\]
만약 더 확신이 있다면 0보다 크다는 조건 보다는 더 좋은 조건을 사용할 수도 있을 것이다. (가령 3보다는 크다 같은…)
어찌되었든 우리는 식 (13)을 만족할 때 새로 추천 받은 $\mu_{new}$를 수용할 것이고 그렇지 못한 경우는 reject 할 것이다.
하지만, MCMC를 이용한 Bayesian Estimation에서도 Sampling method 때와 마찬가지로 패자부활전을 거칠 수 있다.
4. 패자부활전
만약 식 (13)을 만족하지 못한 경우에는 샘플링 method때와 마찬가지로 패자부활전을 거칠 수 있다.
이 때, $[0,1]$의 interval을 가지는 uniform distribution $U_{[0, 1]}$으로부터 추출한 $u$에 대해서 다음을 만족할 경우 $\mu_{new}$로 수용할 수 있다.
추정의 결과
\[\frac{\sum_{i=1}^{N}\left\lbrace-\log(\sigma\sqrt{2\pi})-\frac{(d_i-\mu_{new})^2}{2\sigma^2}\right\rbrace + \log(P(\mu = \mu_{new}))} {\sum_{i=1}^{N}\left\lbrace-\log(\sigma\sqrt{2\pi})-\frac{(d_i-\mu_{old})^2}{2\sigma^2}\right\rbrace + \log(P(\mu = \mu_{old}))} > u
otag\] \[\text{where } u \sim U_{[0, 1]}\]
그림 9를 보면 처음에 $\mu$ 값을 1부터 시작해 서서히 추정해나가면서 모평균인 10에 가까워져 가는 것을 알 수 있다. 약 20 iteration 이후부터 실제 모평균에 가까운 값에서 진동하는 것을 볼 수 있기도 하다.
우리는 보통 이렇게 초기의 iteration 동안 실제 모평균에 수렴하기 위해 거치는 단계를 burn-in period라고 부른다.
그림 9. 처음 50 iteration 동안의 수용되거나 거절된 $\mu$ 값들
그림 10에서는 12,000 iteration 동안 수용되거나 거절된 $\mu$값을 표현하였다.
그림 10을 보면 모평균인 10에서 멀어진 경우가 추천되면 거절되지만 모평균인 10에 가까운 경우가 추천되면 수용된 것을 볼 수 있다.
그림 10. 전체 12,000 iteration 동안의 수용되거나 거절된 $\mu$ 값들
처음의 25% iteration 구간을 burn-in period로 잡고 나머지 75%의 iteration 동안 수용된 $\mu$값을 모두 평균 해 보면 그 값이 9.99 임을 알 수 있었고, 이는 모평균인 10에 매우 가까운 것임을 알 수 있었다.
이렇게 구한 모평균인 9.99를 이용해 모집단의 분포를 추정하면 아래의 그림 11과 같이 원래의 모집단과 매우 유사한 분포를 가진다는 것을 알 수 있을 것이다.
그림 11. 원래의 모집단의 분포와 추정된 $\mu$ 값을 이용해 추정한 모집단의 분포
※ MCMC를 이용한 Bayesian Estimation의 MATLAB 코드는 아래의 위치에서 받아가실 수 있습니다.
https://github.com/angeloyeo/gongdols/tree/master/%ED%86%B5%EA%B3%84%ED%95%99/MCMC/metropolis_hastings/Bayesian_estimation_with_MCMC
참고자료
24. Markov chain Monte Carlo (MCMC) inference
24.1. Introduction
앞 장에서 배웠던 몬테 카를로 법은 고차원에 대해 잘 작동하지 않는다는 점이었다. 고차원 분포에서 샘플링하는 가장 널리 쓰이는 방법은 마르코프 연쇄 몬테 카를로(MCMC)이다. MCMC의 기본 아이디어는 목표하는 확률분포를 정지 분포로 갖는 마르코프 연쇄를 만든 뒤 상태 공간에서 무작위 걸음을 해서 각 상태 에서 소비하는 시간이 에 비례하도록 하는 것이다. 이 연쇄로부터 (상호 연관된) 표본들을 추출함으로써, 에 대한 몬테 카를로 적분을 수행할 수 있게 된다.
변분 추론과 비교하자면, 변분 추론의 이점들은 작은 문제에 대해 더 빠르다는 것, 결정론적이라는 것, 멈출 지점을 판단하기 쉽다는 것, 로그 가능도에 대한 하한을 제공한다는 것이 있다. 마르코프 연쇄 몬테 카를로 샘플링의 이점들은 구현하기 쉽다는 것, 더 넓은 범위의 모델에 적용가능하다는 것, 큰 모델이나 데이터셋에 대해 더 빠르다는 것 등이 있다.
24.2. Gibbs sampling
유명한 마르코프 연쇄 몬테 카를로법으로 깁스 샘플링(깁스 동역학, 열 목욕)이 있다. 이는 좌표 하강법의 마르코프 연쇄 몬테 카를로 버전이다.
24.2.1. Basic idea
기본 아이디어는 각 단계마다 하나의 변수를 다른 변수들은 분포에 존재한다는 조건하에 샘플링을 하는 것이다. 관측가능한 변수면 샘플링하지 않는다.
이 때 은 변수 i에 대한 전체 조건부함수라 불린다. 일반적으로 는 변수들 중 일부에만 의존할 수 있는데, 를 그래프 모델로 나타낸다면 i의 마르코프 담요들을 살펴봄으로써 의존성을 추론할 수 있다. 즉, 를 알기 위해서는 그의 근방만 알면 충분하다. 이런 관점에서 깁스 샘플링은 분산 알고리즘이라 할 수 있다. 하지만 병렬 알고리즘은 아닌데, 샘플들이 순차적으로 추출되어야 하기 때문이다.
그러므로 마르코프 연쇄가 발화되기 전까지는, 즉 정지 분포에 도달하기 전까지는 초기 표본들을 버리는 것이 필요하다.
24.2.2. Example: Gibbs sampling for the Ising model
쌍별 마르코프 무작위 장/조건부 무작위 장은 다음의 형태를 갖는다.
간선 잠재 함수가 인 경우에는 전체 조건부함수를 구하면 이 된다. ( , 즉 근방 노드 중 부호가 같은 노드의 수에서 부호가 다른 노드의 수를 뺀 것에 현재 부호를 곱한 것)
이는 국소적 증거 항 와 결합 가능하다. 예를 들어, 가우시안 관측 모델로 인 경우에는 전체 조건부함수는 이 된다. 즉, 가 각 상태에 진입할 확률은 그 근방과의 유사도와 데이터에 대한 유사도를 모두 고려하게 되는 것이다.
24.2.3. Example: Gibbs sampling for inferring the parameters of a GMM
가우시안 혼합 모델의 매개변수를 깁스 샘플링을 이용해 추론해 보자. 반켤레사전분포를 사용할 때 전체 결합분포는 다음과 같다.
혼합 분포 각각에 대한 사전분포는 통일시킨다. 이 때 전체 조건부 분포는 다음과 같다.
24.2.3.1. Label switching
혼합 모델에서의 깁스 샘플링은 근본적 약점이 있다. 모델의 매개변수 와 지시함수 를 특정할 수 없다는 것이다. 같은 가능도를 도출하는 서로 다른 여러 은닉 라벨의 순열이 존재하기 때문이다. 즉, 표본들의 몬테 카를로 평균을 취하는 것만으로는 사후평균을 계산할 수 없다. 그 대신 모든 최빈값에 대해 평균을 내서 이 모든 k에 대해 같아지는 값을 찾아야 한다. 이를 라벨 변환 문제라 한다.
이 문제는 기대값 최대화나 변분 기대값 최대화 문제에서는 등장하지 않는다. 단일 최빈값에 분포를 가두기 때문이다. 하지만 최빈값이 여러 개인 분포에서는 항상 등장할 수 있는 문제이다. 1차원 문제에서는 매개변수에 대해 조건을 걸어서 특정을 할 수 있다. 하지만 가능도가 사전분포를 압도하게 될 수 있으므로 항상 활용가능한 방법은 아니다. 또한, 고차원으로 확장가능한 방법도 아니다. 다른 방법은 표본들을 후처리해 손실 함수를 최소화하는 순열을 찾는 것이다. 그러나 이 방법은 느리다.
아마도 최선의 방법은 유일하게 결정 가능하지 않은 해답을 갖는 질문을 아예 하지 않는 것이다. 예를 들면 데이터 i가 클러스터 k에 속하는지가 아니라 데이터 i와 데이터 j가 같은 클러스터에 속하는지를 알아보는 방법이 있다. 후자의 문제는 라벨링에 불변이고, 관측가능한 통계량에만 의존한다. 이는 혼합 모델에 대해 확장가능하다는 이점도 있다. 이 경우 은닉 클러스터는 잘 정의되지 않지만 분할은 잘 정의되기 때문이다.
24.2.4. Collapsed Gibbs sampling
일부 경우에 대해서는 미지 변수 중 일부를 적분해 빼내고 나머지만 샘플링하는 방법도 있다. 이를 붕괴 깁스 샘플링이라 한다. 이는 더 저차원에서 샘플링을 하므로 훨씬 더 효과적이다.
정확하게는, 를 샘플링하고 를 적분해 빼낸다고 하자. 는 마르코프 연쇄에 참가하지 않는다. 그러므로 조건부 독립인 표본 들을 추출할 수 있다. 이는 단순 결합분포에서 추출한 샘플들에 비해 훨씬 더 낮은 분산을 갖는다. 이를 라오-블랙웰화라 하며, 다음 정리와 연관이 있다.
Theorem. (Rao-Blackwell) 와 가 연관 확률변수고 가 스칼라 함수라 하자. 그러면 이 성립한다.
이 정리는 를 적분해 빼낸 추정으로부터의 분산이 항상 직접 몬테 카를로 추정을 한 분산 이하임을 보증한다.
24.2.4.1. Example: collapsed Gibbs for fitting a GMM
완전 켤레사전분포를 사용하는 가우시안 혼합 모델을 고려해 보자. 이 경우 를 적분해 빼낼 수 있고, 만 샘플링하면 충분하다. 이 때 전체 조건부함수는 다음과 같아진다.
( 은 클래스 조건분포의 초매개변수)
첫 번째 항은 다음과 같다.
( )
두 번째 항은 다음과 같다.
( )
이 때 에 대한 켤레사전분포를 사용한다면 위의 항을 닫힌 형태로 계산할 수가 있다. 또한, 각 클러스터에 대한 충족 통계량을 구함으로써 예측가능도도 업데이트할 수 있다. 현재 클러스터 에서 의 통계량을 제거한 뒤 각 클러스터의 사후예측분포에서 을 계산하면 된다. 그 방법으로 새 클러스터를 계산한 뒤에, 그 새 클러스터에 의 통계량을 추가하면 된다. 순차적으로 을 샘플링함으로써 샘플을 초기화할 수 있다. 가우시안 혼합 모델의 경우에는 단계마다 시간이 걸린다.
붕괴 깁스 샘플링과 일반 깁스 샘플링을 비교하면 붕괴 샘플링이 일반적으로 더 잘 동작함을 알 수 있다. 하지만, 둘 다 국소적 해에 갇힐 수 있다.
24.2.5. Gibbs sampling for hierarchical GLMs
데이터가 상호 연관된 복수의 소스를 가지고 어떤 소스의 신뢰도가 다른 것들보다 높다면 모든 데이터를 동시에 모델링해서 통계적 세기를 빌려오는 것이 좋을 것이다. 이러한 문제를 푸는 자연스러운 방법은 계층적 베이지안 모델링, 다단계 모델링을 사용하는 것이다. 이에 깁스 샘플링을 사용해 보자.
의 형태를 가질 때, 깁스 샘플링의 전체 조건부 함수는 다음과 같다.
(
이 방법은 정규화를 잘 수행한다.
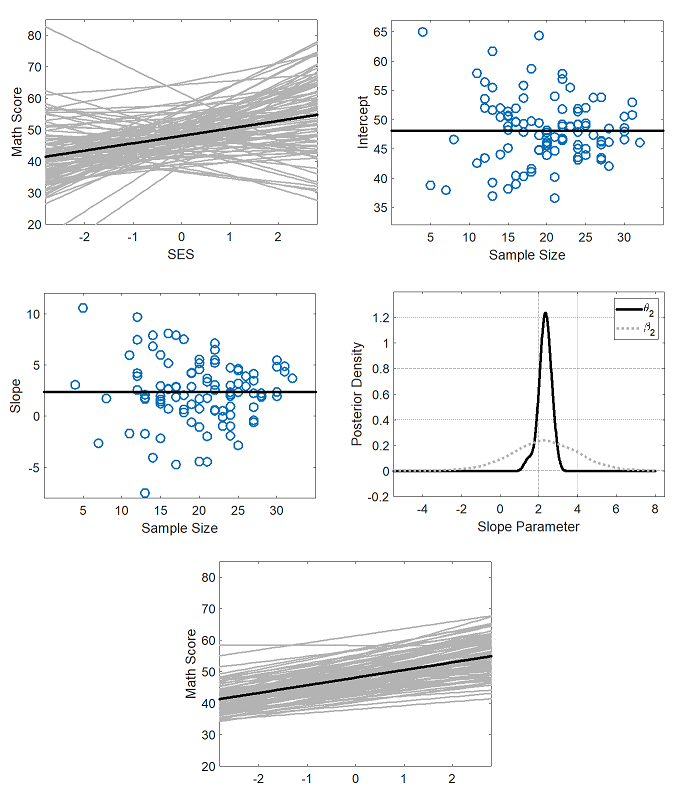
다층 선형 회귀 데모.
24.2.6. BUGS and JAGS
깁스 샘플링의 장점 중 하나는 거의 모든 모델에 적용할 수 있는 소프트웨어를 설계할 수 있다는 것이다. 모델 특정 (그래프 형태)와 전체 조건부함수로부터 샘플링하는 라이브러리만 있으면 된다. 이러한 패키지의 예제는 깁스 샘플링을 사용한 베이지안 업데이트 (BUGS), 또 다른 깁스 샘플러(JAGS) 등이 있다. 그러나 수작업으로 최적화한 코드보다 느리다는 단점이 있다.
24.2.7. The Imputation Posterior (IP) algorithm
전가 사후분포(IP) 알고리즘은 깁스 샘플링의 특수한 경우로, 변수를 두 클래스로 나눈다. 은닉 변수 와 매개변수 . 이는 기대값 최대화의 마르코프 연쇄 몬테 카를로 버전으로, E 단계가 I 단계로, M 단계가 P 단계로 대체된 것이다. 이를 일반화한 것이 데이터 증강이다.
24.2.8. Blocking Gibbs sampling
깁스 샘플링은 한 번에 하나의 변수만 업데이트하므로 (단일 사이트 업데이트) 느릴 수 있다. 변수들의 상호 연관성이 크다면, 현 상태로부터 이동하는 데 오랜 시간이 걸린다. 이동의 크기는 조건부 분포의 분산에 의존한다. 방향의 분산이 l이고 지지집합의 크기가 L이면 독립적인 표본을 얻는 데 단계가 걸린다.
일부 경우에 대해서는 변수의 그룹을 한 번에 업데이트할 수 있다. 이를 블록화 깁스 샘플링 또는 블록 깁스 샘플링이라 불린다.
쏠린 2D 가우시안에 대해 깁스 샘플링의 속도 예제.
24.3. Metropolis Hastings algorithm
깁스 샘플링은 간단하지만 적용가능한 모델이 제한되어 있으며 느리다는 단점이 있다. 그래서 이를 일반화한 메트로폴리스 헤이스팅스(MH) 알고리즘이 있다.
24.3.1. Basic idea
메트로폴리스 헤이스팅스의 기본 발상은 각 단계에서 제안 분포 의 확률로 현 상태 에서 다음 상태 으로 이동하는 것이다. 제안 분포는 특정 조건만 만족한다면 어떻게 골라도 상관없다. 널리 사용되는 분포는 가 있다. 이를 무작위 걸음 메트로폴리스 알고리즘이라 한다. 으로 이전 상태에 의존하지 않는 제안 분포를 만든다면 이를 독립 추출기라 한다. 이는 중요성 추출과 비슷하다.
으로의 이동이 제안된 상태에서, 각 상태에서 보내는 시간의 비율이 에 비례하는지를 체크해서 이 제안을 채택할지 결정할 수 있다. 제안 분포가 대칭적( )이면, 채택 확률은 다음과 같다.
이는 탐욕적 이동뿐만 아니라 하향 이동도 가능하게 한다. 제안 분포가 대칭적이지 않으면 채택 확률은 다음의 헤이스팅스 보정으로 주어진다.
메트로폴리스 헤이스팅스 알고리즘을 유용하게 만드는 중요한 이유 중 하나는 를 계산할 때 그저 대상 분포만 알면 된다는 것이다. 즉 표준화 상수를 알지 못해도 로부터 표본을 추출할 수 있다. 를 점별로 계산하는 것으로 충분하다.
24.3.2. Gibbs sampling is a special case of MH
깁스 샘플링은 메트로폴리스 헤이스팅스의 특수 케이스이다. 정확히는, 의 제안 분포를 사용할 때의 메트로폴리스 헤이스팅스가 바로 깁스 샘플링이다. 이 때 채택 확률은 100%가 되지만 그것이 깁스 샘플링의 수렴성을 보장하는 것은 아니다. 한 번에 하나의 좌표만 업데이트하기 때문이다. 그래서 다른 제안 분포들이 존재한다.
24.3.3. Proposal distribution
대상 분포 에 대해, 제안 분포 가 허용 가능하거나 적절하려면 지지집합이 대상 분포보다 커야 한다. 물론, 제안 분포의 모양도 매우 중요하다. 제안 분포로 가우시안 혼합 모델을 사용하는 경우 분산이 너무 작다면 연쇄는 하나의 최빈값에 갇힌다. 분산이 너무 크다면 대부분의 이동이 기각되고 연쇄는 초기값에 매우 달라붙을 것이다.
깁스 샘플링의 큰 이점은 제안 분포를 따로 고를 필요가 없다는 것이다. 채택률 자체는 크게 중요하지는 않다. 최빈값을 평균으로 갖고 분산이 0인 분포도 채택률은 100%지만 쓸모가 없기 때문이다. 가우시안 커널의 분산을 증가시킴으로써 적절한 채택률을 고를 수가 있는데, 가우시안 대상 분포에 대해서는 25%-40%가 최적인 것으로 알려져 있다. 이렇게 제안 분포를 튜닝하기 위한 짧은 최초의 샘플링들을 파일럿 수행이라 한다.
가우시안 혼합 모델에 대한 마르코프 연쇄 몬테 카를로 vs 메트로폴리스 헤이스팅스.
24.3.3.1. Gaussian proposals
상태 공간이 연속이라면 가우시안 제안 분포의 공분산에는 헤시안 를 국소적 최빈값 에서 구한 값을 쓴다. 이는 헤시안이 국소적 곡률과 각 차원의 길이 스케일을 모델링한다는 점을 이용해서 깁스 샘플링의 느리다는 단점을 보완한다.
두 가지 자연스러운 접근법이 있다. 독립적 제안 을 사용하는 것과 무작위 걸음 제안 을 사용하는 것. 이 때 가 점근적으로 최적임이 알려져 있다. 이 때 채택률은 0.234가 된다.
1D 로지스틱 회귀에 대한 메트로폴리스 헤이스팅스.
24.3.3.2. Mixture proposals
여러 제안 분포를 혼합한 혼합 제안도 있다. 의 형태를 갖는다. ( , 는 올바른 제안 분포)
24.3.3.3. Data-driven MCMC
최적의 제안 분포는 단지 이전 은닉 상태뿐만 아니라 관측 가능한 데이터에도 의존하는 의 형태를 가진다. 이를 데이터 기반 마르코프 연쇄 몬테 카를로라 한다. 이러한 제안 분포를 만들기 위해서는 전방 모델로부터 쌍을 샘플링하고 구별적 분류기를 학습해 을 예측하는 것이다. ( 는 관측 가능한 데이터에서 추출한 특성)
보통 는 고차원이기 때문에 전체 상태 벡터 를 예측하기는 어렵다. 그 대신에 각 상태에 대한 벡터 을 학습한다. 이후 의 제안을 이용한다. 여기서 은 데이터에 독립적인 제안 분포이고 (ex. 무작위 걸음) 는 상태 공간의 k번째 부분을 업데이트한다. 복수 변수에 대한 결합 변화를 제안할 수도 있지만 이는 쉽지 않다.
이 과정은 생성 후 테스트의 형태를 가진다. 구별적 제안 분포 는 새 가설들을 생성하고, 이는 사후분포 비율 을 계산함으로써 테스트된다. 담금질 단계를 추가함으로써, 이 알고리즘은 사후 최빈값을 찾는 데 쓰일 수 있다. 이를 시뮬레이션화된 담금질이라 한다. 이는 제안 분포가 가역적일 필요가 없다는 장점이 있다.
24.3.4. Adaptive MCMC
알고리즘이 진행되는 도중 제안 분포의 매개변수를 변화시킬 수 있다. 이를 적응적 마르코프 연쇄 몬테 카를로라 한다. 이는 처음에는 넓은 공분산으로 시작한 뒤 최빈값을 찾고 나면 공분산을 줄이는 식의 알고리즘을 가능케 한다. 하지만, 마르코프 특성을 깨면 안 된다는 것에 주의할 필요가 있다. 즉, 제안 분포의 매개변수가 연쇄의 전체 기록에 의존하면 안 된다. 이를 보장하는 방법은 매개변수의 적응을 시간에 따라 흐릿하게 하는 것이다.
24.3.5. Initialization and mode hopping
마르코프 연쇄 몬테 카를로를 초기화할 때에는 0이 아닌 확률에서 초기화할 필요가 있다. 모델이 결정론적 제한 조건을 갖고 있다면 이는 어렵기 때문에, 초기화할 때는 대개 국소적 최빈값에서 초기값을 갖도록 하고는 한다. 상태 공간이 이산적이라면 최적화를 여러 번 돌려서 여러 최빈값에서 평균을 내는 것이 효율적이고, 상태 공간이 연속적이라면 최빈값의 확률밀도가 낮으므로 각 최빈값에서 국소적으로 탐색을 하는 것이 필요하다.
24.3.6. Why MH works
메트로폴리스 헤이스팅스 알고리즘은 왜 로부터 표본을 추출하는가? 이 알고리즘은 다음의 전이 행렬에 대한 마르코프 연쇄를 정의한다.
if , 이외엔
이를 분석해 보자. 먼저 연쇄가 을 만족할 경우 세부 균형을 만족한다고 한다. 이 경우 는 그 자체의 저이 분포가 된다. 그리고 다음의 정리에 의해 메트로폴리스 헤이스팅스 알고리즘의 정당성이 보장된다.
Theorem. 메트로폴리스 헤이스팅스 알고리즘에 의해 정의된 전이 행렬이 에르고딕이고 기약이면 는 그 자신의 유일한 제한 분포이다.
24.3.7. Reversible jump (trans-dimensional) MCMC
매개변수의 수가 서로 다른 모델들이 있다고 하다. 모델을 m, 미지수를 이라 하자. 서로 다른 차원을 갖는 공간에서의 샘플링을 차원 변화 마르코프 연쇄 몬테 카를로라 한다. 먼저 모델 지시자 을 샘플링한다. 그 뒤 모든 매개변수를 로부터 추출할 수도 있지만 이는 매우 비효율적이고, 로부터 샘플링하는 것이 효율적이다.
이 접근법의 난점은 서로 다른 차원에서 모델을 이동할 때 발생한다. 메트로폴리스 헤이스팅스 채택율을 계산할 때 서로 다른 공간에서의 확률분포를 비교하게 되므로 의미가 없어지기 때문이다. 그래서 저차원 공간을 추가 확률변수로 증강해 차원을 맞추는 가역 점프 마르코프 연쇄 몬테 카를로(RJMCMC) 등의 방법이 있다. 이는 실제로는 상당히 어렵지만 연속적 매개변수를 적분해 빼낼 수 있다면 이산적 상태 공간만 남기 때문에 훨씬 더 쉬워진다. 이를 붕괴 가역 점프 마르코프 연쇄 몬테 카를로라 한다. 이를 이용해 연관 벡터 기계나 보조 벡터 기계에 대한 베이지안적 대안을 제공하는 것도 가능하다.
24.4. Speed and accuracy of MCMC
마르코프 연쇄 몬테 카를로와 관련된 이론적, 실제적 이슈를 알아보자.
24.4.1. The burn-in phase
정지 분포에 도달하기 이전 추출된 표본들은 버려진다. 이를 발화 단계라 한다. 이 단계를 결정하는 것은 어려운데, 이것은 마르코프 연쇄 몬테 카를로법의 약점이기도 하다.
무작위 걸음의 예제.
24.4.2. Mixing rates of Markov chains
마르코프 연쇄가 수렴하는 데 걸리는 시간을 혼합 시간이라 부른다. 즉, 상태 으로부터 혼합 시간은 모든 에 대해 이 되는 최소 시간이다. (T는 전이 행렬) 이 때 혼합 시간은 으로 정의된다. 를 전이 행렬의 첫 번째 고유값과 두 번째 고유값의 차라고 할 때, 임이 알려져 있다.
다른 접근법은 상태 공간의 모양을 조사해 보는 것이다. 연쇄의 전도도를 로 정의할 때, 즉 해당 집합에서 다른 집합으로 전이할 확률의 최소치로 정의할 때 임이 알려져 있다. 즉, 전도도가 낮을 수록 혼합 시간은 길어진다. 최빈값이 잘 분리된 분포라면 전도도가 낮고 혼합 시간은 길어질 것이다.
24.4.3. Practical converge diagnostics
연쇄의 혼합 시간을 계산하는 것은 일반적으로 매우 어렵다. 전이 행렬의 계산이 어렵기 때문이다. 실제로는 수렴을 진단하는 휴리스틱이 많이 쓰이는데, 실제로 수렴성을 정확히 판단해 주지는 못한다. 간단한 방법 중 하나는 과분산된 시작점으로부터 여러 연쇄를 시작시킨 뒤 추적 플롯을 찍어봐서 같은 지점으로 수렴했는지 알아보는 것이다.
24.4.3.1. Estimated potential scale reduction (EPSR)
수렴의 정도를 정량적으로 알아볼 수 있는 방법은 다음과 같다. 기본 발상은 각각 연쇄에서의 분산과 연쇄들간의 분산을 비교하는 것이다. 발화 이후 D개의 변수를 가진 C개의 연쇄로부터 각각 S개의 샘플 를 추출하고 를 로부터 유도되는 관심 있는 스칼라값이라 하면 수열 평균과 전체 평균을 , 로 정의하자. 수열간 분산과 수열 내 분산을 , 로 정의하면, 이라 할 때 W와 는 를 각각 과소추정, 과대추정한다. 이로부터, 추정 잠재 크기 감소량(EPSR) 로 정의하면 계속 샘플링을 했을 때 사후분산이 감소할지 아닐지를 판단할 수 있다. 이라면 이 추정은 신뢰할만 하다고 할 수 있다.
24.4.4. Accuracy of MCMC
마르코프 연쇄 몬테 카를로로부터 추출되는 표본들은 자동으로 상호 연관되므로 독립적인 표본들이 가지는 정보량을 감소시킨다. 이를 정량화하면 다음과 같다. 어떤 함수 에 대해 일 때 의 평균을 구하고 싶다고 하자. 평균의 참값을 이라고 하고 이에 대한 몬테 카를로 추정을 이라 하자. 이 추정의 분산에 대한 마르코프 연쇄 몬테 카를로 추정은 다음과 같다.
이는 자동 상호 연관 함수(ACF) 을 정의해 측정할 수 있다. 이는 n번째마다 샘플을 보존하는 솎아내기로 계산을 쉽게 할 수 있다. 유효 표본수(ESS) 을 정의하면 표본의 집합의 정보량을 이로부터 추정할 수 있다.
24.4.5. How many chains?
그래서 몇 개의 연쇄를 수행해야 할까? 보통은 3개 정도의 연쇄를 각각 길이 100000 정도로 수행하고 표본의 첫 절반을 버린 뒤 표본을 취한다. 국소적 최빈값으로 초기값을 잡으면 발화를 기다리느라 표본의 첫 절반을 버리지 않아도 될 것이다.
24.5. Auxiliary variable MCMC
가끔 더미 보조 변수를 써서 원본 변수들 사이의 상호 연관을 줄여 샘플링의 효율성을 비약적으로 높일 수 있다. 원본 변수를 , 보조 변수를 라고 할 때 여야 하고 가 보다 더 샘플링하기 쉬울 수 있기 때문이다. 이후에는 그냥 를 버리면 된다.
24.5.1. Auxillary variable sampling for logistic regression
프로빗 회귀의 잠재 변수 표현은 다음과 같다.
이는 보조 변수 깁스 샘플링으로 치환하기 쉽다.
로지스틱 회귀에 대해서는 어떻게 할까? 가 로지스틱 분포 를 따른다고 하면 이 된다. 이 때 , 로부터 샘플링을 함으로써 보조 변수 깁스 샘플링을 할 수 있다. 로부터 직접 샘플링하는 것은 불가능하기 때문에, 한 가지 방법은 , 에 대해 (KS는 콜모고로프 스미르노프 분포), 를 샘플링하는 것이다. 더 간단한 방법은 로지스틱 분포를 스튜던트 분포로 근사하는 것이다. , 로 근사를 한 뒤 스튜던트 분포의 가우시안 혼합 표현으로 추론을 간략화하는 것이다. 즉, 다음이 성립한다.
이 때 로 두면 이 되어 프로빗 회귀와 동치가 된다. 프로빗 회귀냐 로짓 회귀냐를 선택하는 대신에 를 추정할 수 있다. 적합한 켤레사전분포는 없지만 유한한 범위의 가능한 값들을 고려한 뒤 사후분포를 로 구하면 된다. 로 놓으면 도 샘플링할 수 있다.
24.5.2. Slice sampling
일변수 다최빈값 분포 를 생각해 보자. 보조 변수 u를 더해 이동의 크기를 크게 할 수 있다. 결합분포를 if , ( ) 이외 0으로 정의하면 x에서의 주변분포는 이 된다. 그러므로 로부터 샘플링한 뒤 u를 무시하면 로부터 샘플링할 수 있다. 전체 조건부분포는 다음과 같다.
( )
이를 절단 샘플링이라 한다. 실제로는 집합 A를 구하기 어렵다. 그래서 적당한 점 근처의 구간 를 잡은 뒤 각 끝점이 절단부에 위치하는지 본다. 위치할 경우에는 절단면 밖으로 빠져나올 때까지 그 끝점을 확장시킨다 (스텝 아웃). 이후 후보 값 이 그 지역으로부터 균일하게 선택된다. 그 변수가 절단면 내에 있으면 으로 유지시킨다. 그렇지 않으면 영역을 축소해 이 끝점 중 하나가 되면서 을 포함하도록 한다. 이후 표본을 하나 더 추출한다. 이를 표본이 채택될 때까지 반복한다.
이를 다변수 분포로 확장하려면 각 변수마다 보조 변수를 써야 한다. 이 접근법이 깁스 샘플링에 비해 갖는 이점은 전체 조건부를 알아야 할 필요가 없으며 비표준화 결합분포만 알면 충분하다는 점이다. 메트로폴리스 헤이스팅스 알고리즘에 비해 갖는 이점은 제안 분포를 특정해 줘야 할 필요가 없다는 점이다.
1D 절단 샘플링.
2D 절단 샘플링.
24.5.3. Swendsen Wang
, (e는 간선) 꼴의 아이싱 모델을 생각해 보자. 간선 세기 J가 클 때 인접한 노드끼리의 상호 연관성이 클 수 있기 때문에 깁스 샘플링은 느릴 수 있다. 스웬젠 왕 알고리즘은 이에 보조 변수를 도입해서 훨씬 속도를 빠르게 하는 마르코프 연쇄 몬테 카를로 법이다.
각 간선마다 이진 보조 변수 (결합 변수) 를 도입한 뒤 확장 모델 , 가 되도록 잡으면 이 된다. 즉 이 확장 모델에서 샘플링을 한 뒤 를 버리면 된다. 이 모델에 대해서는 깁스 샘플링을 적용하기 쉽다. 각각의 결합 변수가 정점 변수에 대해 조건부독립이므로 전체 조건부 함수가 간선에 대해 인수분해되기 때문이다. 전체 조건부함수 의 계산도 쉽다. 간선의 양 끝 정점의 상태가 같다면 을 의 확률로 놓는다. 아니면 으로 놓는다.
을 샘플링하려면 가동된 결합변수들로부터 정의되는 그래프의 연결요소를 찾은 뒤 그 중 하나를 고르고 그 연결 요소 전체를 무작위 상태로 바꿔버린다.
직관적으로 스웬젠 왕 알고리즘은 깁스 샘플링보다 상태 공간에서 갖는 이동의 크기가 크다. 간선 세기가 온도 T에 대해 일 때 온도가 크면 깁스 샘플링이나 스웬젠 왕 알고리즘이나 똑같이 잘 동작하지만, 온도가 임계 온도 에 도달할 때에는 상호 연관 길이가 대단히 길어지고 깁스 샘플링이 독립적인 표본을 추출하는 데 매우 오래 걸리게 된다. 반면, 스웬젠 왕 알고리즘은 모든 온도에서 상태를 빠르게 혼합한다.
단, 간선 세기 중 단 하나라도 음수이면 이 계는 좌절계가 되어 스웬젠 왕 알고리즘이 잘 작동하지 못한다. 인접한 변수들끼리 같은 변수를 갖도록 강요하는데, 이것이 자연스럽지 않기 때문이다.
24.5.4. Hybrid/Hamiltonian MCMC
연속된 상태 공간에서 로그 사후분포의 경사를 구함으로써 마르코프 연쇄 몬테 카를로 샘플링을 하는 방법이 있다. 기본 발상은 매개변수를 공간 내 입자로 보고 보조 변수를 이 입자의 모멘텀으로 정의하는 것이다. 그리고 이 매개변수-모멘텀 쌍을 특정한 규칙에 따라 업데이트하는 것이다. 이를 혼성 마르코프 연쇄 몬테 카를로 또는 해밀토니언 마르코프 연쇄 몬테 카를로법이라 한다. 이 때 사용자는 업데이트를 할 널뛰기 횟수와 그 크기를 지정해 줘야 한다. 이는 추계적 경사 하강법과 혼합되어 큰 데이터셋을 다룰 수도 있다.
24.6. Annealing methods
많은 분포는 최빈값이 여러 개여서 샘플링하기 쉽지 않다. 하지만, 계산적 온도 변수를 통해 분포를 다듬질하는 방법이 있다.
24.6.1. Simulated annealing
모의 담금질법은 모르는 함수 의 전역 최적해를 찾는 추계적 알고리즘이다. 이는 메트로폴리스-헤이스팅스 알고리즘과 연관이 있으며, 이산적/연속적 최적화에 모두 쓰일 수 있다.
이는 통계물리학에서 비롯되었다. 핵심 통계량은 상태 에 존재할 확률을 특정하는 볼츠만 분포 인데 ( 은 계의 에너지, T는 온도) 온도가 0에 접근할 수록 계는 최소 에너지 상태에 머무르게 된다. 높은 온도에서는 표면이 평면에 가까워지므로 이동을 하기 쉬워진다. 이후 온도를 식힘으로써 작은 고점들을 사라지게 하고 큰 고점들을 돌출시킨다. 이를 통해 가장 큰 고점을 추적함으로써 전역 최적해를 찾을 수 있다. 이를 연속화법이라 한다.
이를 서술하면 다음과 같다. 각 단계마다, 적절한 제안 분포 에서 새 상태를 샘플링한다. 이후, 을 정의한 뒤, 새 상태를 확률로 채택하고 이외 확률로 기각한다 (현상태 유지)
시간에 따라 온도를 변화시키는 냉각 계획을 정확히 정하기는 쉽지 않은데 (이것이 담금질 법의 중요한 단점 중 하나다), 대개 지수적 냉각 계획 을 사용한다. 대개 , 이다.
모의 담금질법 예제.
24.6.2. Annealed importance sampling
모의 담금질 법과 중요도 샘플링을 혼합해 어려운 분포로부터 독립적 표본들을 추출하는 법을 담금질된 중요도 샘플링이라 한다. 이 샘플링하기 어려운 함수이고 은 샘플링하기 쉬운 함수라고 가정하자. 이 때, 온도의 역수 에 대해 중간 분포 , 를 만들어 으로부터 에 접근하는 수열들을 만드는 것이다. 거기다 각각에 불변한 마르코프 연쇄 들을 가진다고 하자. 이 때, 으로부터 을 샘플링하는 것은 다음과 같이 수행할 수 있다.
먼저 을 다음과 같이 샘플링한다. 을 샘플링하고, 을 샘플링하고, 이를 반복해 을 샘플링한다. 마지막으로 으로 두고 가중치 을 부여하면 된다.
24.6.3. Parallel tempering
마르코프 연쇄 몬테 카를로와 담금질을 결합하는 다른 방법은 여러 연쇄를 서로 다른 온도에서 병렬로 수행한 뒤 한 연쇄에서 인접한 연쇄로부터 샘플링을 하는 것이다. 이 방법에서는 고온을 가진 연쇄는 저온을 가진 연쇄에 영향을 줄 수 있게 된다. 이를 병렬 템퍼링이라 한다.
24.7. Approximating the marginal likelihood
주변가능도 를 어떻게 근사할까?
24.7.1. The candidate method
간단한 방법은 후보 방법으로 의 특성을 이용하는 것이다. 이는 임의의 에 대해 성립하기 때문에 적절한 값을 선택해 와 을 쉽게 계산할 수 있다. 근처에서 사후분포 추정을 한다면 분모도 계산할 수 있다. 이는 대개 마르코프 연쇄 몬테 카를로로 근사된다.
이 방법의 단점은 이 사후분포의 모든 최빈값에 대해 주변화된다는 불확실한 가정을 하고 있다는 점인데, 그래서 실 성능은 그다지 좋지 못하다.
24.7.2. Harmonic mean estimate
다음과 같이 근사하는 방법이 있다.
그러나 이 방법도 사후분포로부터 추출된 표본에만 의존한다는 단점이 있다. 사후분포는 사전분포에 민감하지 않지만 가능도는 사전분포에 민감하기 때문에 이도 실 성능은 매우 떨어진다.
24.7.3. Annealed importance sampling
중요도 샘플링을 통해 분할 함수의 비율을 구할 수 있다.
( )
을 사후분포, 을 사전분포로 넣으면 사전분포의 표준화 상수 을 알 때 을 추정할 수 있다.
요점 정리
마르코프 연쇄 몬테 카를로(MCMC) : 고차원 분포에서 샘플링하는 가장 널리 쓰이는 방법으로, 목표하는 확률분포를 정지 분포로 갖는 마르코프 연쇄를 만든 뒤 상태 공간에서 무작위 걸음을 해서 각 상태에서 소비하는 시간이 목표 분포에 비례하도록 하고 이 연쇄로부터 표본을 추출한다.
깁스 샘플링 : 각 단계마다 하나의 변수를 다른 변수들은 분포에 존재한다는 조건하에 샘플링을 하는 것이다. 관측가능한 변수면 샘플링하지 않는다.
메트로폴리스 헤이스팅스 알고리즘 : 각 단계에서 제안 분포의 확률로 현 상태에서 다음 상태 로 이동하는 것
마르코프 연쇄 몬테 카를로 법의 속도와 정확성을 측정하는 여러 지표가 있다.
더미 변수를 추가해 샘플링하는 보조 변수 마르코프 연쇄 몬테 카를로 법이 존재한다.
계를 고온으로 만들어 표면을 평평하게 한 뒤 저온으로 식혀 전역 해를 찾는 담금질 법이 존재한다.
마르코프 연쇄 몬테 카를로법에서 여러 방법으로 주변가능도를 근사할 수 있다.
So you have finished reading the 마르코프 연쇄 몬테카를로 방법 topic article, if you find this article useful, please share it. Thank you very much. See more: 마르코프 연쇄 설명, 마르코프 체인, MCMC 알고리즘, 쉽게 쓰여진 MCMC, 몬테카를로 시뮬레이션 확률분포, 마르코프 가정, Metropolis-Hastings 알고리즘, MCMC 수렴

