Top 27 삼각 함수 각 의 변환 The 117 Correct Answer

You are looking for information, articles, knowledge about the topic nail salons open on sunday near me 삼각 함수 각 의 변환 on Google, you do not find the information you need! Here are the best content compiled and compiled by the Chewathai27.com/to team, along with other related topics such as: 삼각 함수 각 의 변환 삼각함수 각변환 암기, 삼각함수 각변환 증명, 삼각함수 각변환 예각, 삼각함수 각변환 공식, Cos sin 변환, 삼각함수 각변환 둔각, 삼각함수 90도 공식, Sin, cos 변환 공식

삼각함수 각의 변환

나오는 각을 + θ 또는 90°n + θ로 바꾼다. 이때, n은 정수, 0 < θ <
n이 짝수이면 sin → sin. …
+ θ 또는 90°n + θ가 몇 사분면의 각이냐에 따라 +, -를 붙인다. 올 – 싸 – 탄 – 코 (all – sin – tan – cos)

삼각함수 각변환 공식 8분만에 이해시켜드립니다 – 무작정 외우지 마세요

삼각함수 각의 변환 총정리 – 수학방

Article author: mathbang.net
Reviews from users: 20882 Ratings
Top rated: 4.8
Lowest rated: 1
Summary of article content: Articles about 삼각함수 각의 변환 총정리 – 수학방 Updating …
Most searched keywords: Whether you are looking for 삼각함수 각의 변환 총정리 – 수학방 Updating 삼각함수는 기본적으로 sin, cos, tan의 세 가지예요. 거기에 각도 기본적인 θ에 -θ, 2nπ ± θ, π ± θ, ± θ로 7가지가 더 있어요. 그래서 기본 삼각함수 3개에 삼각함수 각의 변환 21개까지 총 24가지가..
Table of Contents:

삼각함수 각의 변환 총정리

댓글(16개) 펼치기닫기

Article author: mathbang.net
Reviews from users: 16977 Ratings
Top rated: 3.6
Lowest rated: 1
Summary of article content: Articles about 삼각함수 각의 변환 2 – π ± θ, π/2 ± θ – 수학방 삼각함수는 기본적으로 sin, cos, tan의 세 가지인데, 거기에 π ± θ와 로 네 개의 각이 나오죠? 그러니까 총 12가지 변환하는 내용이 나와요. 게다가 θ, -θ에 관한 내용도 … …
Most searched keywords: Whether you are looking for 삼각함수 각의 변환 2 – π ± θ, π/2 ± θ – 수학방 삼각함수는 기본적으로 sin, cos, tan의 세 가지인데, 거기에 π ± θ와 로 네 개의 각이 나오죠? 그러니까 총 12가지 변환하는 내용이 나와요. 게다가 θ, -θ에 관한 내용도 … 삼각함수의 각의 변환 두 번째예요. 삼각함수 각의 변환 1 – 2nπ ± θ, -θ에서는 θ가 2nπ + θ일 때와 -θ일 때를 공부해봤는데요. 이 글에서는 θ가 π ± θ일 때와 일 때를 공부할 거예요. 삼각함수는 기..
Table of Contents:

삼각함수 각의 변환 2 – π ± θ π2 ± θ

댓글(5개) 펼치기닫기

Article author: calcproject.tistory.com
Reviews from users: 28328 Ratings
Top rated: 4.0
Lowest rated: 1
Summary of article content: Articles about [수학I] 15. 삼각함수 공식 : 삼각함수 사이의 관계, 삼각함수 변환 (개념+수학문제) 이번 학습지는 사분면 위에 있는 각에 대하여 삼각함수를 다른 삼각함수로 고치는 문제입니다. sin과 cos이 주어진 경우에는 각각 cos과 sin을 구한 후, … …
Most searched keywords: Whether you are looking for [수학I] 15. 삼각함수 공식 : 삼각함수 사이의 관계, 삼각함수 변환 (개념+수학문제) 이번 학습지는 사분면 위에 있는 각에 대하여 삼각함수를 다른 삼각함수로 고치는 문제입니다. sin과 cos이 주어진 경우에는 각각 cos과 sin을 구한 후, … [2020-09-23] 수정 학습지 빠른 정답의 일부 내용이 문제와 달라 수정하였습니다. | 같이 보면 좋은 글 📄 [수학I] 삼각함수(sin,cos,tan)의 뜻 | 삼각함수 사이의 관계 [정리] 삼각함수 사이의 관계는 다음과..
Table of Contents:

알리미

태그

공지사항

카테고리

★

최근글

삼각함수 각의 변환 총정리

삼각함수는 기본적으로 sin, cos, tan의 세 가지예요. 거기에 각도 기본적인 θ에 -θ, 2nπ ± θ, π ± θ, ± θ로 7가지가 더 있어요. 그래서 기본 삼각함수 3개에 삼각함수 각의 변환 21개까지 총 24가지가 있어요.

물론 각의 변환 21가지를 다 외울 수 있으면 외우면 좋아요. 하지만 외우기에는 개수도 너무 많고 헷갈리죠. 그래서 이걸 한 번에 총정리하는 시간이 필요합니다. 특히 이 모든 걸 한 방에(?) 해결할 수 있는 공식이 있으니까 꼭 외웠다가 상황에 맞게 적용하세요.

삼각함수 각의 변환 총정리

삼각함수 각의 변환은 앞서 했던 삼각함수 각의 변환 1 – 2nπ ± θ, -θ, 삼각함수 각의 변환 2 – π ± θ, π/2 ± θ에서 그 이유와 결과를 공부했어요.

하지만 과정이 조금 복잡하고 개수도 많고 비슷비슷해서 헷갈리기가 쉽죠. 이 모든 경우에 한번에 적용할 수 있는 공식(?)이 있어요. 물론 공식을 안다고 해서 계산이 쉬워지는 건 아니지만 변환 과정은 조금 쉬워질 겁니다.

앞서 공부했던 내용들을 이용해서 이 과정이 나오게 된 이유를 생각해보는 것도 좋을 것 같아요.

나오는 각을 + θ 또는 90°n + θ 로 바꾼다.

이때, n은 정수, 0 < θ < 또는 0 < θ < 90° n이 짝수이면 바꾸지 않는다. sin → sin cos → cos tan → tan n이 홀수이면 바뀐다. sin → cos cos → sin tan → + θ 또는 90°n + θ 가 몇 사분면의 각이냐에 따라 +, -를 붙인다. 올 - 싸 - 탄 - 코 (all - sin - tan - cos) 다음을 구하여라. (1) sin120° × cos150° × tan210° (2) sinθ = , cosθ = , tanθ = 일 때, (단, 0 < θ < ) (1) 삼각함수별로 따로 나눠서 생각해보죠. sin120° = sin(90° × 1 + 30°) n = 1로 홀수니까 sin → cos, 120°는 제 2 사분면의 각으로 sin은 (+)부호를 가져요. sin120° = sin(90° × 1 + 30°) = cos30° = cos150° = cos(90° × 1 + 60°) n = 1로 홀수이므로 cos → sin, 150°는 제 2 사분면의 각으로 cos은 (-) 부호를 가져요. cos150° = cos(90° × 1 + 60°) = -sin60° = - tan210° = tan(90° × 2 + 30°) n = 2로 짝수니까 tan → tan, 210°는 제 3 사분면의 각으로 tan는 (+) 부호를 가져요. tan210° = tan(90° × 2 + 30°) = tan30° = sin120° × cos150° × tan210° = (2)도 따로 나눠서 보죠. n = 1로 홀수니까 sin → cos, + θ는 제 2 사분면의 각으로 sin은 (+) 부호를 가져요. n = 2로 짝수니까 cos → cos, π + θ는 제 3 사분면의 각으로 cos은 (-) 부호를 가져요. n = 3으로 홀수니까 tan → , + θ는 제 4 사분면의 각으로 tan는 (-) 부호를 가져요. 하나로 다 모으면 함께 보면 좋은 글 삼각함수 각의 변환 1 - 2nπ ± θ, -θ 삼각함수 각의 변환 2 - π ± θ, π/2 ± θ 삼각함수 사이의 관계 호도법, 라디안(radian) 일반각, 시초선, 동경, 양의 각, 음의 각, 사분면의 각 정리해볼까요 삼각함수 각의 변환 나오는 각을 + θ 또는 90°n + θ 로 바꾼다. 이때, n은 정수, 0 < θ < n이 짝수이면 sin → sin cos → cos tan → tan n이 홀수이면 sin → cos cos → sin tan → + θ 또는 90°n + θ 가 몇 사분면의 각이냐에 따라 +, -를 붙인다. 올 - 싸 - 탄 - 코 (all - sin - tan - cos) 그리드형(광고전용)

삼각함수 각의 변환 2 – π ± θ, π/2 ± θ

삼각함수의 각의 변환 두 번째예요. 삼각함수 각의 변환 1 – 2nπ ± θ, -θ에서는 θ가 2nπ + θ일 때와 -θ일 때를 공부해봤는데요. 이 글에서는 θ가 π ± θ일 때와 일 때를 공부할 거예요.

삼각함수는 기본적으로 sin, cos, tan의 세 가지인데, 거기에 π ± θ와 로 네 개의 각이 나오죠? 그러니까 총 12가지 변환하는 내용이 나와요. 게다가 θ, -θ에 관한 내용도 있어서 양도 많고 상당히 헷갈리는 내용이니까 그림과 설명을 하나씩 잘 짚어가면서 공부해야 해요.

삼각함수 각의 변환

π ± θ 의 삼각함수

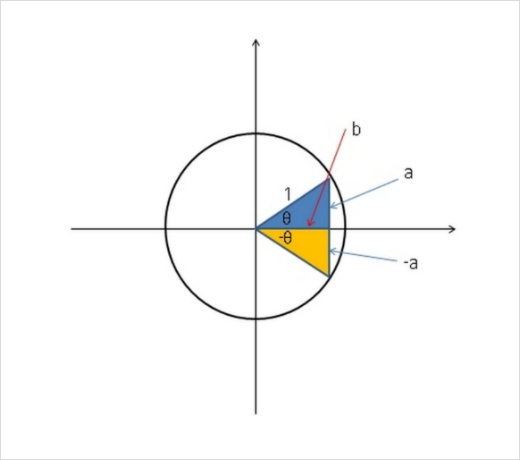
θ와 π + θ의 삼각함수를 비교해보죠.

그림을 보면 알 수 있겠지만 θ를 나타내는 동경과 π+ θ를 나타내는 동경은 서로 원점에 대하여 대칭이에요. 점 P의 좌표를 (x, y)라고 하고 점 P’의 좌표를 (x’, y’)라고 한다면 점 P와 점 P’는 원점에 대하여 대칭이므로 부호가 서로 반대예요.

x’ = -x

y’ = -y

다른 방법으로 생각해보죠. 원점에 대하여 대칭이면 제 1 사분면의 각은 제 3 사분면의 각이 되고, 제 2 사분면의 각은 제 4 사분면의 각이 돼요. 제 1 사분면 ↔ 제 3 사분면, 제 2 사분면 ↔ 제 4 사분면

올 – 싸 – 탄 – 코 (all – sin – tan – cos) 에서 tan 함수는 제 1, 3 사분면의 부호가 (+)로 같고, 제 2, 4 사분면의 부호는 (-)로 같아요. tan은 원점에 대하여 대칭일 때는 부호가 같다는 얘기지요. 따라서 θ가 π + θ가 되어도 tan의 부호는 그대로 인 거예요. sin과 cos는 원점에 대하여 대칭이 아니기 때문에 θ가 π + θ가 되면 부호가 반대로 바뀌어요.

sin( π + θ ) = -sin θ

+ ) = -sin cos( π + θ ) = -cos θ

+ ) = -cos tan( π + θ ) = tan θ

이번에는 π – θ의 삼각함수를 알아보죠. 위의 π + θ에서 θ를 -θ로 바뀌기만 하면 돼요.

sin(π – θ) = sin{π + (-θ)} = -sin(-θ) = sin(θ)

cos(π – θ) = cos{π + (-θ)} = -cos(-θ) = -cos(θ)

tan(π – θ) = tan{π + (-θ)} = tan(-θ) = -tan(θ)

의 삼각함수

이번에는 의 삼각함수를 알아보죠.

앞서 했던 여러 삼각함수에서는 대칭이동이었는데, 이번에는 대칭이동이 아니에요.

점 P의 좌표를 (x, y)라고 하고 점 P’의 좌표를 (x’, y’) 한다면 이 둘 사이에는 어떤 관계가 생길까요? x’ = -y, y’ = x의 관계가 성립해요. 이 관계가 어떻게 나오는지 잘 이해하셔야 해요.

x’ = -y

y’ = x

이번에는 의 삼각함수를 알아보죠. 위의 에서 θ를 -θ로 바뀌기만 하면 돼요.

지금까지 삼각함수의 각의 변환을 공부해봤는데, sin, cos, tan 세 가지에다 부호까지 엄청나게 헷갈리죠? 물론 이걸 다 외우면 좋겠지요. 하지만 너무 헷갈려서 외우기가 어렵다면 굳이 외울 필요는 없어요.

이걸 쉽게 변환하는 방법은 삼각함수 각의 변환 총정리에서 다뤄보기로 하죠.

함께 보면 좋은 글

삼각함수 각의 변환 1 – 2nπ ± θ, -θ

삼각함수 사이의 관계

삼각함수의 뜻, 삼각함수의 정의, sin, cos, tan, 삼각함수 값의 부호

호도법, 라디안(radian)

일반각, 시초선, 동경, 양의 각, 음의 각, 사분면의 각

정리해볼까요 삼각함수 각의 변환, π ± θ sin( π + θ ) = -sin θ

+ ) = -sin cos( π + θ ) = -cos θ

+ ) = -cos tan( π + θ ) = tan θ 삼각함수 각의 변환,

그리드형(광고전용)

[수학I] 15. 삼각함수 공식 : 삼각함수 사이의 관계, 삼각함수 변환 (개념+수학문제)

[2020-09-23] 수정

학습지 빠른 정답의 일부 내용이 문제와 달라 수정하였습니다.

| 같이 보면 좋은 글

📄 [수학I] 삼각함수(sin,cos,tan)의 뜻

| 삼각함수 사이의 관계
[정리] 삼각함수 사이의 관계는 다음과 같습니다.
[정리] 삼각함수는 동경이 나타내는 사분면에 따라 부호가 정해집니다.

제 1사분면 : 모두(sinθ,cosθ,tanθ) 양수

제 2사분면 : sinθ이 양수

제 3사분면 : tanθ가 양수

제 4사분면 : cosθ이 양수

| 삼각함수 변환하기

삼각함수를 다른 삼각함수로 고쳐봅시다.

이 문제는 코사인 값을 이용해 사인 값을 구한 뒤, 두 값을 바탕으로 탄젠트 값을 구해야 합니다.

위 방법으로 문제를 풀면 다음과 같습니다.

이 문제는 탄젠트 값을 바탕으로 사인과 코사인 값을 알아내야 합니다.

| 학습지 미리보기

| 첨부파일

2020SP H2-15.pdf 0.15MB

| 닫는 말

삼각함수 사이의 관계는 두 공식을 통해 나타낼 수 있습니다. 공식을 활용하면 삼각함수를 다른 삼각함수로 고칠 수 있습니다. 이번 학습지는 사분면 위에 있는 각에 대하여 삼각함수를 다른 삼각함수로 고치는 문제입니다.

sin과 cos이 주어진 경우에는 각각 cos과 sin을 구한 후, tan값을 구해야 합니다.tan가 주어진 경우에는 sin^2+cos^2=1임을 이용하여 sin과 cos값을 도출할 수 있습니다.

✔ 저작물 관련 유의사항

– 본 저작물(문제 및 그림)은 학습지 제작소에 있으며, 비상업적, 상업적 이용이 가능합니다.

– 저작물을 사용 시 출처를 밝힌 후, 자유롭게 사용이 가능합니다.

– 학습지제작소의 저작물을 2차 배포하거나, 제 3자에게 제공하거나, 또는 출판하는 행위(ISBN이 포함된 서적으로 출판)는 엄격히 금지합니다.

Copyright. 2020. 학습지제작소. All Rights Reserved.

더보기 #태그 : 삼각함수, sin, cos, tan, 사인 코사인 탄젠트 바꾸기, 변환하기, 고치기, 삼각함수 사이의 관계, 삼각함수 공식, 학습지, 무료, 다운, 다운로드, 고2, 고등학교 2학년, 수학I, 수학1, 학습지제작소

So you have finished reading the 삼각 함수 각 의 변환 topic article, if you find this article useful, please share it. Thank you very much. See more: 삼각함수 각변환 암기, 삼각함수 각변환 증명, 삼각함수 각변환 예각, 삼각함수 각변환 공식, Cos sin 변환, 삼각함수 각변환 둔각, 삼각함수 90도 공식, Sin, cos 변환 공식

Top 27 삼각 함수 각 의 변환 The 117 Correct Answer

삼각함수 각의 변환 총정리 – 수학방

삼각함수 각의 변환 2 – π ± θ, π/2 ± θ – 수학방

[수학I] 15. 삼각함수 공식 : 삼각함수 사이의 관계, 삼각함수 변환 (개념+수학문제)

삼각함수 각변환

[삼각함수 기초 #5] 삼각함수 각도 변환 cos(90˚-θ), sin(90˚-θ), tan(90˚-θ) 값 구하기

삼각함수 각의 변환 총정리

삼각함수 각의 변환 2 – π ± θ, π/2 ± θ

[수학I] 15. 삼각함수 공식 : 삼각함수 사이의 관계, 삼각함수 변환 (개념+수학문제)

Leave a Comment Cancel reply