Top 12 단면 1 차 모멘트 The 102 Latest Answer

You are looking for information, articles, knowledge about the topic nail salons open on sunday near me 단면 1 차 모멘트 on Google, you do not find the information you need! Here are the best content compiled and compiled by the Chewathai27.com/to team, along with other related topics such as: 단면 1 차 모멘트 단면 2차 모멘트, 단면 1차 모멘트 문제, 단면1차모멘트 계산, 단면1차모멘트 용도, 단면 1차 모멘트 Q, t형 단면 1차 모멘트, 단면모멘트 의미, 1차 모멘트 2차 모멘트 차이

단면 일차 모멘트는 축으로부터 도심점까지의 거리에 면적을 곱한것을 말한다. 단위는 길이의 세제곱이다. 평면 도형의 도심을 구하기 위하여 사용된다.

---

도심 단면 1차 모멘트 한번에 잡자 / FE 시험 / 재료역학 기본 / Mechanics of Materials – Part 2 (도심 단면 1차 모멘트)

도심 단면 1차 모멘트 한번에 잡자 / FE 시험 / 재료역학 기본 / Mechanics of Materials – Part 2 (도심 단면 1차 모멘트)

---

단면 일차 모멘트 – 위키백과, 우리 모두의 백과사전

• Article author: ko.wikipedia.org
• Reviews from users: 27876 Ratings
• Top rated: 4.9
• Lowest rated: 1
• Summary of article content: Articles about 단면 일차 모멘트 – 위키백과, 우리 모두의 백과사전 Updating …
• Most searched keywords: Whether you are looking for 단면 일차 모멘트 – 위키백과, 우리 모두의 백과사전 Updating
• Table of Contents:

정의[편집]

특성[편집]

도심[편집]

같이 보기[편집]

각주[편집]

참고 문헌[편집]

외부 링크[편집]

Read More

Class 18. 단면 1차 모멘트 (S)

• Article author: mmstudycafe.tistory.com
• Reviews from users: 36560 Ratings
• Top rated: 4.4
• Lowest rated: 1
• Summary of article content: Articles about Class 18. 단면 1차 모멘트 (S) Class 18 · 1. 단면 1차 모멘트의 단위는 길이단위의 세제곱이다. · 2. 단면 1차 모멘트의 값은 축의 위치에 따라 달라질 수 있다. · 3. 축이 도심의 연장 … …
• Most searched keywords: Whether you are looking for Class 18. 단면 1차 모멘트 (S) Class 18 · 1. 단면 1차 모멘트의 단위는 길이단위의 세제곱이다. · 2. 단면 1차 모멘트의 값은 축의 위치에 따라 달라질 수 있다. · 3. 축이 도심의 연장 … Class 18 안녕하세요. 오늘도 어김없이 밍밍한 공부방을 찾아주신 여러분 감사드립니다. 저번 시간으로 정역학 시간은 모두 마무리 되었습니다. 이번 시간부터는 구조역학으로 들어가 보도록 하겠습니다. 저희가..
• Table of Contents:

Class 18

태그

‘건축이야기건축구조’ Related Articles

티스토리툴바

Read More

[재료역학] 단면 1차 모멘트(First moment of area)와 도심(Centroid)

• Article author: study2give.tistory.com
• Reviews from users: 1873 Ratings
• Top rated: 4.2
• Lowest rated: 1
• Summary of article content: Articles about [재료역학] 단면 1차 모멘트(First moment of area)와 도심(Centroid) 아래와 같은 그림에서 단면 1차모멘트에 대해 알아봅시다. 단면 1차모멘트는 축으로부터 도심점까지의 거리에 면적을 곱한것인데요 … …
• Most searched keywords: Whether you are looking for [재료역학] 단면 1차 모멘트(First moment of area)와 도심(Centroid) 아래와 같은 그림에서 단면 1차모멘트에 대해 알아봅시다. 단면 1차모멘트는 축으로부터 도심점까지의 거리에 면적을 곱한것인데요 … 이번 포스팅에선 단면 1차모멘트와 도심에 대해 알아봅시다.  단면 1차모멘트와 도심 아래와 같은 그림에서 단면 1차모멘트에 대해 알아봅시다. 단면 1차모멘트는 축으로부터 도심점까지의 거리에 면적을 곱한것..혼자 공부하는 공대출신 직장인의 블로그입니다.
• Table of Contents:

[재료역학] 단면 1차 모멘트(First moment of area)와 도심(Centroid)

단면 1차모멘트와 도심

다양한 도형 형태에서의 도심

티스토리툴바

Read More

09.단면 1차 모멘트(Geometrical moment of area)

• Article author: mathmecha.tistory.com
• Reviews from users: 47046 Ratings
• Top rated: 3.5
• Lowest rated: 1
• Summary of article content: Articles about 09.단면 1차 모멘트(Geometrical moment of area) 5. 단면 1차 모멘트 … 즉, 도심이란 각각의 면적에 기준축에서의 거리를 곱해 가중치를 주고 전부 합한 후 다시 전체 면적으로 나눈 값이다. 이 때, 식.1에서 각 면적과 … …
• Most searched keywords: Whether you are looking for 09.단면 1차 모멘트(Geometrical moment of area) 5. 단면 1차 모멘트 … 즉, 도심이란 각각의 면적에 기준축에서의 거리를 곱해 가중치를 주고 전부 합한 후 다시 전체 면적으로 나눈 값이다. 이 때, 식.1에서 각 면적과 … >>> 단면 1차 모멘트(Geometrical moment of area) 강의 바로가기 <<< 1. 단면 1차 모멘트는? ​- 단면: 물체, 구조물의 보이는 단면 (2차원 평면) ​- 1차: 단면에 관한 첫 번째 모멘트 정의 (큰 의미 없..
• Table of Contents:

태그

관련글

댓글6

티스토리툴바

Read More

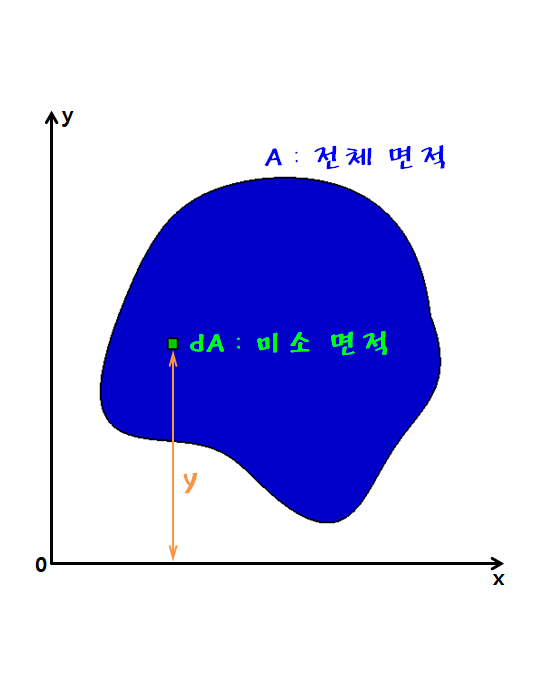
단면 1차 모멘트의 모든것 – 도심 , 합성단면 등

• Article author: new-material.tistory.com
• Reviews from users: 12208 Ratings
• Top rated: 3.6
• Lowest rated: 1
• Summary of article content: Articles about 단면 1차 모멘트의 모든것 – 도심 , 합성단면 등 위의 그림에서 생각해 보겠습니다. 우선 단면 1차 모멘트라 하면 의미는 따로 없습니다. 이것으로 도심이나 극관성모멘트 등을 구할 수 있는 하나의 … …
• Most searched keywords: Whether you are looking for 단면 1차 모멘트의 모든것 – 도심 , 합성단면 등 위의 그림에서 생각해 보겠습니다. 우선 단면 1차 모멘트라 하면 의미는 따로 없습니다. 이것으로 도심이나 극관성모멘트 등을 구할 수 있는 하나의 … 위의 그림에서 생각해 보겠습니다. 우선 단면 1차 모멘트라 하면 의미는 따로 없습니다. 이것으로 도심이나 극관성모멘트 등을 구할 수 있는 하나의 도구라고 생각하시면 편할 것 같습니다. 단면 1차모멘트는 축..
• Table of Contents:

단면 1차 모멘트의 모든것 – 도심 합성단면 등 본문

티스토리툴바

Read More

---

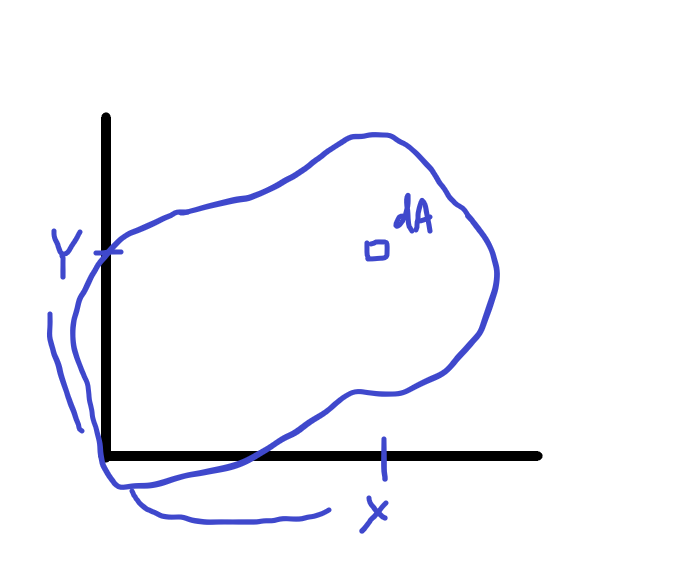
See more articles in the same category here: https://chewathai27.com/to/blog.

단면 일차 모멘트

단면 일차 모멘트는 축으로부터 도심점까지의 거리에 면적을 곱한것을 말한다. 단위는 길이의 세제곱이다. 평면 도형의 도심을 구하기 위하여 사용된다.

정의 [ 편집 ]

임의 형상의 단면에 대해서, 미소 면적 dA를 생각하고, 직교 좌표축으로부터 미소면적 도심까지 거리를 곱한 다음 전체 면적에 대해 적분을 하면 단면 1차 모멘트(G)다.

G x = ∫ A y d A = A ⋅ y ¯ {\displaystyle G_{x}=\int _{A}ydA=A\cdot {\bar {y}}} G y = ∫ A x d A = A ⋅ x ¯ {\displaystyle G_{y}=\int _{A}xdA=A\cdot {\bar {x}}}

여기서 x ¯ , y ¯ {\displaystyle {\bar {x}},{\bar {y}}} 를 각각의 축에서부터 단면의 도심까지 거리라고 한다.

특성 [ 편집 ]

단면 1차 모멘트는 축의 위치에 따라 양의 값을 가질수도, 음의 값을 가질수도 있다. 도심을 지나는 축에 대한 단면 1차 모멘트는 0이다.

도심 [ 편집 ]

도심(centroid)이란 어떤 임의 단면에서 직교 좌표축에 대한 단면 1차 모멘트가 0이 되는 점을 말한다. 직교 좌표축에서 도심까지의 거리를 구하는 방법은 단면 1차 모멘트를 도형의 면적으로 나누면 된다.

x ¯ = G y A {\displaystyle {\bar {x}}={\frac {G_{y}}{A}}} y ¯ = G x A {\displaystyle {\bar {y}}={\frac {G_{x}}{A}}}

대표적인 도형의 도심 [ 편집 ]

도형 그림 x ¯ {\displaystyle {\bar {x}}} y ¯ {\displaystyle {\bar {y}}} 면적 삼각형 b 3 {\displaystyle {\frac {b}{3}}} h 3 {\displaystyle {\frac {h}{3}}} b h 2 {\displaystyle {\frac {bh}{2}}} 사각형 b 2 {\displaystyle {\frac {b}{2}}} h 2 {\displaystyle {\frac {h}{2}}} b h {\displaystyle bh} 사분원[1] 4 r 3 π ( = 2 D 3 π ) {\displaystyle {\frac {4r}{3\pi }}(={\frac {2D}{3\pi }})} 4 r 3 π ( = 2 D 3 π ) {\displaystyle {\frac {4r}{3\pi }}(={\frac {2D}{3\pi }})} π r 2 4 {\displaystyle {\frac {\pi r^{2}}{4}}} 반원[2] 0 {\displaystyle \,\!0} 4 r 3 π ( = 2 D 3 π ) {\displaystyle {\frac {4r}{3\pi }}(={\frac {2D}{3\pi }})} π r 2 2 {\displaystyle {\frac {\pi r^{2}}{2}}}

포물선의 도심 [ 편집 ]

y = h ( 1 − x 2 b 2 ) {\displaystyle y=h\left(1-{\frac {x^{2}}{b^{2}}}\right)} 포물선의 도심을 x ¯ , y ¯ {\displaystyle {\overline {x}},\ {\overline {y}}} 라고 하자. 포물선의 미소한 면적 dA는

d A = y d x = h ( 1 − x 2 b 2 ) d x {\displaystyle dA=ydx=h\left(1-{\frac {x^{2}}{b^{2}}}\right)dx}

포물선의 면적 공식에 의해

A = 2 3 b h {\displaystyle A={\frac {2}{3}}bh}

단면일차모멘트부터 계산한다.

Q x = ∫ y 2 d A = ∫ 0 b h 2 2 ( 1 − x 2 b 2 ) 2 d x = 4 15 b h 2 {\displaystyle {\begin{aligned}Q_{x}=\int {\frac {y}{2}}dA&=\int _{0}^{b}{\frac {h^{2}}{2}}\left(1-{\frac {x^{2}}{b^{2}}}\right)^{2}dx\\&={\frac {4}{15}}bh^{2}\\\end{aligned}}}

Q y = ∫ x d A = ∫ 0 b h x ( 1 − x 2 b 2 ) d x = 1 4 b 2 h {\displaystyle {\begin{aligned}Q_{y}=\int xdA&=\int _{0}^{b}hx\left(1-{\frac {x^{2}}{b^{2}}}\right)dx\\&={\frac {1}{4}}b^{2}h\\\end{aligned}}}

도심 계산

x ¯ = G y A = 1 4 b 2 h 2 3 b h = 3 8 b {\displaystyle {\begin{aligned}{\overline {x}}={\frac {G_{y}}{A}}&={\frac {{\frac {1}{4}}b^{2}h}{{\frac {2}{3}}bh}}\\&={\frac {3}{8}}b\\\end{aligned}}}

y ¯ = G x A = 4 15 b h 2 2 3 b h = 2 5 h {\displaystyle {\begin{aligned}{\overline {y}}={\frac {G_{x}}{A}}&={\frac {{\frac {4}{15}}bh^{2}}{{\frac {2}{3}}bh}}\\&={\frac {2}{5}}h\\\end{aligned}}}

같이 보기 [ 편집 ]

각주 [ 편집 ]

참고 문헌 [ 편집 ]

전찬기, 이종헌, 정환호, 김운학, 김경진 (2015). 《토목기사 과년도 시리즈 응용역학》. 성안당. 77-78쪽. ISBN 978-89-315-6807-3 .

Gere, Goodno. 〈도심과 관성모멘트의 복습〉. 《재료역학》 8판. Cengage Learning.

외부 링크 [ 편집 ]

Class 18. 단면 1차 모멘트 (S)

Class 18

안녕하세요.

오늘도 어김없이 밍밍한 공부방을 찾아주신 여러분 감사드립니다.

저번 시간으로 정역학 시간은 모두 마무리 되었습니다.

이번 시간부터는 구조역학으로 들어가 보도록 하겠습니다.

저희가 지금까지 지점반력, 단면력을 구하고

단면력도를 그려왔습니다.

이제는 단면 자체에 더 집중을 해서

단면의 성질에 따라서 구조물이 어떻게 거동하는지에 대해

살펴보도록 할 것입니다.

오늘은 단면의 성질 중 첫번째로

단면 1차 모멘트에 대해서 알아볼 것입니다.

우선, 단면 1차 모멘트의 정의는 다음과 같습니다.

“임의 형상의 단면에 대해서, 미소 면적 dA를 생각하고,

직교 좌표로부터의 거리(x 혹은 y)를 곱한 다음

전체 면적에 대해 적분을 하면 단면 1차 모멘트 이다.”

그리고 단면 1차 모멘트를 구하는 식은 다음과 같습니다.

말이 되게 어렵죠??

더 간단하게 말해드리자면

단면 1차 모멘트란

(단면적) × (축으로부터 도심까지의 거리) 입니다.

문제를 하나 풀어보시면

더 이해가 잘 가실거에요.

그럼 문제를 풀어보도록 하겠습니다.

단면 1차 모멘트는

단면적 × 축으로부터 도심까지의 거리라고 말씀 드렸는데

축으로부터 도심까지의 거리는

X축에 대한 단면 1차 모멘트를 구할 때에는 y 값(세로)으로,

Y축에 대한 단면 1차 모멘트를 구할 때에는 x 값(가로)으로 해주시면 됩니다.

그럼 위의 문제는 다음과 같이 구할 수 있습니다.

이 문제에서 알 수 있는 것은 무엇일까요?

1. 단면 1차 모멘트의 단위는 길이단위의 세제곱이다.

2. 단면 1차 모멘트의 값은 축의 위치에 따라 달라질 수 있다.

3. 축이 도심의 연장선상에 위치한다면 단면 1차 모멘트의 값은 0이다.

단면의 단면적은 정해진 것인 반면에,

축의 위치에 따라 도심까지의 거리는 변할 수 있습니다.

즉, 축의 위치에 따라 단면 1차 모멘트의 값도 변할 수 있습니다.

다음 문제로 넘어가 보겠습니다.

여기까지는 잘 따라올 수 있으시겠죠??

하지만 단면이 사각형 모양만 있는게 아니겠죠??

정방형, 장방형, 삼각형, 원 등 우리가 알고 있던 도형이 아닌

전혀 다른 모양의 단면이 나올 수도 있습니다.

그래서 필요한게 정의에 나와 있었던 적분식입니다.

그럼 적분식으로 직사각형 단면의

단면 1차모멘트를 증명해보도록 하겠습니다.

이걸 적분식을 이용해서 풀이하면 다음과 같습니다.

정의에 나온대로

미소면적(dA)을 설정하고

dA를 y에 대한 식으로 바꿔준다음에

면적이 있는 범위에 맞춰 적분을 해주면

값이 똑같이 나오는 것을 볼 수 있습니다.

이 적분식을 이용하면 단면의 모양이 이상하게 생겼더라도

구할 수 있습니다.

또 단면 1차모멘트의 특성이 하나 더 있는데

단면 1차 모멘트는 축의 위치에 따라 ( + ), ( – )를 구분합니다.

X축에 대한 단면 1차 모멘트를 구할 때는

X축 위에 있으면 ( + ), 아래에 있으면 ( – )이고

Y축에 대한 단면 1차 모멘트를 구할 때는

Y축 오른쪽에 있으면 ( + ), 왼쪽에 있으면 ( – )입니다.

마지막으로

단면 1차 모멘트는 단면을 잘라서 구할 수도 있습니다.

위와 같은 문제는

다음과 같이 단면을 직사각형 두개로 나눠서 구할 수 있습니다.

그럼 다시 한 번 단면 1차 모멘트의 특성을 정리해 보겠습니다.

1. 단면 1차 모멘트의 단위는 길이단위의 세제곱이다.

2. 단면 1차 모멘트의 값은 축의 위치에 따라 달라질 수 있다.

3. 축이 도심의 연장선상에 위치한다면 단면 1차 모멘트의 값은 0이다.

4. 단면 1차 모멘트는 축의 위치에 따라 ( + ), ( – )를 구분한다.

5. 단면 1차 모멘트는 단면을 잘라서 구할 수 있다.

그럼 여러가지 문제와 풀이 올려드릴테니까

여러분도 직접 풀어 보셨으면 좋겠어요.

그럼 이해가 더 잘 되실거에요.

이렇게 해서 단면 1차 모멘트를 살펴보았습니다.

다음 시간에는 단면 1차 모멘트를 이용해서

도심을 구하는 연습을 해보도록 하겠습니다.

오늘도 수고 많으셨습니다.

그럼 다음 시간에 만나요~~~!!!

댓글과 공감은 저에게 엄청난 힘이 됩니다.

댓글 많이 남겨주시고 공감 버튼도 한번씩 꾸욱 눌러주세요!!

구독도 많이 많이 부탁드려요!!!~~

[재료역학] 단면 1차 모멘트(First moment of area)와 도심(Centroid)

반응형

이번 포스팅에선 단면 1차모멘트와 도심에 대해 알아봅시다.

단면 1차모멘트와 도심

아래와 같은 그림에서 단면 1차모멘트에 대해 알아봅시다.

단면 1차모멘트는 축으로부터 도심점까지의 거리에 면적을 곱한것인데요.

영어로는 First moment of area 라고 합니다.

주로 도심을 구하고자 할 때 자주 계산합니다.

도심은 Centroid 이죠.

단면 1차 모멘트는 각 축에 대해 존재하며, 구하는 방법은 아래와 같습니다.

여기서 x ̅, y ̅는 각 축방향의 무게중심입니다.

이 식에 의하면 축이 도심을 지날 때 단면 1차모멘트는 0이 됩니다.

그리고 이 식을 정리하면 단면 1차모멘트를 통해 아래처럼 무게중심을 계산할 수 있습니다.

여기서 A는 전체 면적입니다.

다양한 도형 형태에서의 도심

아래에 여러 도형에 대한 도심을 표시하였으니 참고하세요.

도심 기준 축만 바뀌지 않으면 아래의 결과를 그대로 써먹을 수 있습니다!

여기까지 단면 1차모멘트에 대해 알아보았습니다.

반응형

So you have finished reading the 단면 1 차 모멘트 topic article, if you find this article useful, please share it. Thank you very much. See more: 단면 2차 모멘트, 단면 1차 모멘트 문제, 단면1차모멘트 계산, 단면1차모멘트 용도, 단면 1차 모멘트 Q, t형 단면 1차 모멘트, 단면모멘트 의미, 1차 모멘트 2차 모멘트 차이