You are looking for information, articles, knowledge about the topic nail salons open on sunday near me 두꺼운 렌즈 공식 on Google, you do not find the information you need! Here are the best content compiled and compiled by the Chewathai27.com/to team, along with other related topics such as: 두꺼운 렌즈 공식
이는 ‘렌즈에서의 빛의 굴절’의 s01와 si2의 관계식에서 so1=∞와 si2=BFL로 놓은 것이다.
Table of Contents
µÎ²¨¿î ·»Áî
- Article author: physica.gnu.ac.kr
- Reviews from users: 42861
Ratings
- Top rated: 4.9
- Lowest rated: 1
- Summary of article content: Articles about µÎ²¨¿î ·»Áî Updating …
- Most searched keywords: Whether you are looking for µÎ²¨¿î ·»Áî Updating
- Table of Contents:

·»ÁîÀÇ °á»ó
- Article author: physica.gnu.ac.kr
- Reviews from users: 22475
Ratings
- Top rated: 3.6
- Lowest rated: 1
- Summary of article content: Articles about ·»ÁîÀÇ °á»ó 그러나 두꺼운 렌즈도 근사적으로는 얇은 렌즈의 행동을 한다고 볼 수 있다. … 이 식은 렌즈로부터 물체와 상까지의 거리에 대한 관계로서 가우스 렌즈공식(Gaussian … …
- Most searched keywords: Whether you are looking for ·»ÁîÀÇ °á»ó 그러나 두꺼운 렌즈도 근사적으로는 얇은 렌즈의 행동을 한다고 볼 수 있다. … 이 식은 렌즈로부터 물체와 상까지의 거리에 대한 관계로서 가우스 렌즈공식(Gaussian …
- Table of Contents:

렌즈 공식 유도_Derivation of the lens formula_Thin lens_Power notation
- Article author: kkulnari.tistory.com
- Reviews from users: 46151
Ratings
- Top rated: 3.3
- Lowest rated: 1
- Summary of article content: Articles about 렌즈 공식 유도_Derivation of the lens formula_Thin lens_Power notation Derivation of the lens formula◁ -렌즈 공식 유도- 이번 글은 Thin lens에 대한, 렌즈 공식과 렌즈 제작자 공식(lens makers’ formula), … …
- Most searched keywords: Whether you are looking for 렌즈 공식 유도_Derivation of the lens formula_Thin lens_Power notation Derivation of the lens formula◁ -렌즈 공식 유도- 이번 글은 Thin lens에 대한, 렌즈 공식과 렌즈 제작자 공식(lens makers’ formula), … ▷Derivation of the lens formula◁ -렌즈 공식 유도- 이번 글은 Thin lens에 대한, 렌즈 공식과 렌즈 제작자 공식(lens makers’ formula), 2가지에 관하여 알아볼 것이다. 가우시안 공식(Gaussian formula)과 Co..
- Table of Contents:
태그
‘꿀나리의 광학 이야기 ★’ Related Articles
티스토리툴바
두꺼운 렌즈 공식
- Article author: koreascience.or.kr
- Reviews from users: 26464
Ratings
- Top rated: 4.6
- Lowest rated: 1
- Summary of article content: Articles about 두꺼운 렌즈 공식 얇은 렌즈란 일반적으로 두 개의 구면으로 구성되며 … 로서 이를 렌즈제작자 공식(lens maker’s formu- … 실제로 두꺼운 렌즈나 여러 개 렌즈로 구성된 복합렌. …
- Most searched keywords: Whether you are looking for 두꺼운 렌즈 공식 얇은 렌즈란 일반적으로 두 개의 구면으로 구성되며 … 로서 이를 렌즈제작자 공식(lens maker’s formu- … 실제로 두꺼운 렌즈나 여러 개 렌즈로 구성된 복합렌.
- Table of Contents:

두꺼운 렌즈 공식 뜻: 얇은 렌즈로 어림할 수 없을 때에 사용하는 일반적인 렌즈 공식. 렌즈의 곡률, 초점 거리,
- Article author: wordrow.kr
- Reviews from users: 23065
Ratings
- Top rated: 3.5
- Lowest rated: 1
- Summary of article content: Articles about 두꺼운 렌즈 공식 뜻: 얇은 렌즈로 어림할 수 없을 때에 사용하는 일반적인 렌즈 공식. 렌즈의 곡률, 초점 거리, 두꺼운 렌즈 공식: 얇은 렌즈로 어림할 수 없을 때에 사용하는 일반적인 렌즈 공식. 렌즈의 곡률, 초점 거리, 굴절률 따위와 관련된다. (어휘 혼종어 물리 ) …
- Most searched keywords: Whether you are looking for 두꺼운 렌즈 공식 뜻: 얇은 렌즈로 어림할 수 없을 때에 사용하는 일반적인 렌즈 공식. 렌즈의 곡률, 초점 거리, 두꺼운 렌즈 공식: 얇은 렌즈로 어림할 수 없을 때에 사용하는 일반적인 렌즈 공식. 렌즈의 곡률, 초점 거리, 굴절률 따위와 관련된다. (어휘 혼종어 물리 ) 두꺼운 렌즈 공식: 얇은 렌즈로 어림할 수 없을 때에 사용하는 일반적인 렌즈 공식. 렌즈의 곡률, 초점 거리, 굴절률 따위와 관련된다. (어휘 혼종어 물리 )
- Table of Contents:
🤞
두꺼운 렌즈 공식 두꺼운lens公式
얇은 렌즈로 어림할 수 없을 때에 사용하는 일반적인 렌즈 공식 렌즈의 곡률 초점 거리 굴절률 따위와 관련된다
▹초성이 같은 단어들
▹실전 끝말 잇기
▹시작 또는 끝이 같은 단어들
▹
🦉 이런 동물 속담도 있었네
wordrowkr

렌즈 종류 [정보통신기술용어해설]
- Article author: www.ktword.co.kr
- Reviews from users: 18482
Ratings
- Top rated: 4.1
- Lowest rated: 1
- Summary of article content: Articles about 렌즈 종류 [정보통신기술용어해설] Convex Lens, 볼록 렌즈, 수렴 렌즈, Concave Lens, 오목 렌즈, 발산 렌즈, Thin Lens, 얇은 렌즈, Thick Lens, 두꺼운 렌즈, GRIN 렌즈 · 1. 렌즈 구분 : … …
- Most searched keywords: Whether you are looking for 렌즈 종류 [정보통신기술용어해설] Convex Lens, 볼록 렌즈, 수렴 렌즈, Concave Lens, 오목 렌즈, 발산 렌즈, Thin Lens, 얇은 렌즈, Thick Lens, 두꺼운 렌즈, GRIN 렌즈 · 1. 렌즈 구분 : … 정보통신용어,정보통신사전,차재복
- Table of Contents:
![렌즈 종류 [정보통신기술용어해설]](https://i0.wp.com/wpsites.net/wp-content/uploads/2014/06/icon-after-more-link.png)
See more articles in the same category here: Chewathai27.com/to/blog.
두꺼운 렌즈
두꺼운 렌즈 실제의 렌즈 지금까지 다룬 렌즈는 두께를 무시할 수 있는 경우로서 이때에는 비교적 단순한 공식으로 렌즈에서의 광선의 행동 을 이해할 수 있었다. 그러나 실제의 렌즈는 두께를 가지고 있을 수 밖에 없고, 특히 볼록렌즈 의 경우 가운데가 볼록하므로 곡률반경이 작아지면 광축 에서의 두께는 이제 무시할 수 없게 된다. 이를 두꺼운 렌즈 (thick lens)라 하여 얇은 렌즈 (thin lens)와 구별한다. 렌즈의 두 면에서의 굴절을 주요면 한 면에서의 굴절로 볼 수 있다. 두꺼운 렌즈 에서도 한 점에서 나온 빛이 평행광선이 되는 물체초점과 평행광선이 한 점에 모여드는 상초점을 도입할 수 있는 데 일반적으로 이 두 지점은 렌즈의 중심에 대해 대칭의 점이 아니다. 따라서 하나의 초점거리를 도입하기가 어렵게 되는 데 이러한 난점을 해소할 수 있는 방법으로 두 종류의 주요면 (principal plane)을 도입한다. 주요면 은 렌즈의 앞뒤 표면에서 두 번 굴절하는 것을 한 번의 굴절로 해석할 수 있는 가상적인 면으로 아래 그림들에서 볼 수 있는 것처럼 일반적으로 곡면이다. 주요면 으로는 물체초점에서 나온 빛에 대한 것이 제1주요면 (first principal plane)이다. 또 다른 하나는 광축 에 나란한 평행광선에 대한 것이 제2주요면 (second principal plane)이다. 실제로 물체초점에서 나온 빛이 렌즈의 중심에서 멀리 벗어나서 굴절하는 경우 광축 에 나란한 평행광선이 되지 않는다. 마찬가지로 평행광선이 입사하더라도 역시 중심에서 벗어난 경우에는 상초점으로 모여들지 않는다. 따라서 일반적으로 두 주요면 은 평면이 되지 않고 광축 에 대해 회전대칭인 곡면을 이루게 될 것이다. 아래 두 프로그램은 주요면 을 광선추적 으로 결정하는 방식을 보여준다. ‘리셋’ 버튼으로 임의의 곡률과 두께를 가진 렌즈가 생성되며 각각 물체초점에서 나온 구면파 와 평행광선이 렌즈에 입사하여 굴절하며 최종적으로 한 번의 굴절로 볼 수 있는 지점을 결정하여 이를 이어서 곡면을 형성하게 된다. 그림에서는 녹색의 곡선이 주요면 이다. 한편 두꺼운 렌즈 라 하더라도 근축광선 의 행동은 비교적 명확하다. 즉 물체초점에서 나온 빛은 평행광선이 되고, 아울러 평행광선은 상초점에 정확하게 모여든다. 그리고 이 광선에 대한 주요면 은 거의 평면이다. 화면에서 이 평면을 푸른 수직의 직선으로 나타내었고, 아울러 그 위치도 표시하고 있다. (그림을 ‘크게보기’로 하면 주요면 이 결정되는 원리를 보다 자세히 살펴볼 수 있다) sim
두꺼운 렌즈의 제1주요면 _ 두꺼운 렌즈 의 초점에서 나온 빛이 두꺼운 렌즈 에 입사해서 평행광선으로 나간다. 렌즈의 굴절률 은 1.5, 배경은 1.0으로 고정하였고, ‘리셋’을 누를 때마다 렌즈의 곡률반경과 두께가 임의의 값으로 바뀌어 지면서 광선의 진행 을 볼 수 있다.
sim
두꺼운 렌즈의 제2주요면 _ 두꺼운 렌즈 에 평행광선이 두꺼운 렌즈 에 입사해서 초점에 모여든다. 렌즈의 굴절률 은 1.5, 배경은 1.0으로 고정하였고, ‘리셋’을 누를 때마다 렌즈의 곡률반경과 두께가 임의의 값으로 바뀌어 지면서 광선의 진행 을 볼 수 있다.
주요면으로부터의 두 초점거리는 동일하게 주어진다. 주요면 을 도입한 이유는 무엇일까? 렌즈가 두꺼워지면서 초점거리를 매기는 기준점이 모호해진다. 우선 각 정점 $V_1$과 $V_2$로부터 각 초점까지의 거리를 매길 수 있다. 렌즈의 앞 경계면에서 물체초점까지의 거리가 제1초점거리 라 하고, 렌즈의 뒤 경계면에서 상초점까지의 거리를 제2초점거리 라 한다. 이들은 각각 두 렌즈의 조합 에서와 같이 전방초점거리 (front focal length, FFL)와 후방초점거리 (back focal length, BFL)라 하기도 한다. 예를들어 후방초점거리 는 다음과 같이 조금 복잡한 공식으로 표현된다. \[ \frac{1}{\text{BFL}} = (n-1) \left[ \frac{1}{R_1} \left( \frac{1}{1- \frac{n-1}{n} \frac{d}{R_1}} \right) – \frac{1}{R_2} \right] \] 이는 ‘렌즈에서의 빛의 굴절’의 $s_{01}$와 $s_{i2}$의 관계식에서 $s_{o1} = \infty$와 $s_{i2}=\text{BFL}$로 놓은 것이다. 한편 $R_1 \rightarrow -R_2$, $R_2 \rightarrow -R_1$로 하면 대칭성에 의해 FFL에 대한 관계로 될 것이다. sim
두꺼운 렌즈의 주요면 _ 두꺼운 렌즈 의 두 주요면 을 작도로 보여준다. 아래 위는 모두 동일한 렌즈로 위 그림에서 제2주요면 을, 아래 그림에서 제1주요면 을 작도하고 있다. 따라서 위의 상은 상초점을, 아래의 상은 물체초점의 위치를 보여준다. 편의상 아래 그림을 생성할 때에는 오른쪽에서 왼쪽으로 진행하는 광선으로 하였으나 실제로는 반대 방향으로 진행하는 빛으로 이해하면 된다. 이 그림으로 제1주요면 과 상초점까지의 거리와 제2주요면 과 물체초점과의 거리가 항상 거의 같게 계산되는 것을 알 수 있다.
이와 같이 두 초점거리가 서로 다른데 초점거리를 주요면 과의 거리로부터 매긴다면 두 초점과의 거리가 일치하는 흥미로운 결과가 나온다. 즉 제1주요면 으로부터 물체초점과의 거리와 제2주요면 과 상초점까지의 거리가 같아지는 것이다. 따라서 이를 그저 초점거리라고 부를 수 있게 되는 데 이는 다음과 같이 주어진다. \[ \frac{1}{f} = (n-1) \left[ \frac{1}{R_1} – \frac{1}{R_2} + \frac{(n-1)d}{n R_1 R_2} \right] \] 이제 제1주요면 에서 물체까지의 거리를 $s_o$, 제2주요면 에서 상까지의 거리를 $s_i$라 한다면 두 거리에 대한 관계는 다시 가우스 렌즈공식 으로 돌아간다. \[ \begin{equation} \label{eq3} \frac{1}{s_o} + \frac{1}{s_i} = \frac{1}{f} \end{equation} \] graphic
두꺼운 렌즈의 결상 _ 두꺼운 렌즈 에서 물체의 결상에 대한 도해이다. 그림에서 두꺼운 렌즈 의 중요한 지점, 거리 등의 기호를 보여주고 있으며, 왼쪽 물체에서 나온 세 가닥의 광선이 상을 맺는 것을 결정하는 과정을 보여준다. 기하광학에서 부호의 약속 을 따라서 음양의 부호를 매기되 $h_1, h_2$는 모두 각 정점 $V_1, V_2$의 오른편에 있을 때를 양으로 삼도록 한다.
위 그림은 두꺼운 렌즈 에서 물체의 상을 작도하는 방법과 각각의 거리에 대해 기호로 표시하는 방법을 보여준다. 두꺼운 렌즈 가 가지고 있는 특별한 점으로 물체초점($F_o$), 상초점($F_i$)이 있고, 또한 주요면 이 광축 과 만나는 주요점 (principal point)이 있다. 주요점 은 제1주요면 과 만나는 제1주요점 ($H_1$)과 제2주요면 과 만나든 제2주요점 ($H_2$)이 있다. 한편 렌즈의 광심 을 통과하는 광선은 입사광선과 나란한 방향으로 나가게 되는 데 입사광선과 출사광선을 연정한 선이 광축 과 만나는 두 개의 점이 마디점 (nodal point)이다. 렌즈를 공기 중에서 사용하는 보통의 경우처럼 렌즈의 앞뒤 매질의 굴절률 이 같은 경우에는 이 두 마디점 이 두 주요점 과 일치하게 된다. 따라서 주요면 의 성질, 광심 의 성질 등을 이용하면 얇은 렌즈 에서와 비슷하게 세 광선으로 상이 맺는 지점을 정할 수 있다. 1. 광축 에 나란한 광선은 제2주요면 에서 굴절해서 상초점($F_i$)으로 향한다. 2. 물체초점($F_o$)을 지난 광선은 제1주요면 에서 굴절해서 광축 에 나란하게 진행한다. 3. 제1주요점 ($H_1$)으로 입사한 광선은 제2주요점 ($H_2$)에서 그 방향이 변하지 않고 진행한다.
[질문1] 상초점거리 를 제2주요면 에서, 물체초점거리 를 제1주요면 에서 재면 두 값이 일치하는 것을 보여라. [질문2] 얇은 렌즈 는 렌즈의 위치와 두 주요면 이 일치하는 것을 설명하라. [질문3] 상과 물체초점거리 를 $f$라고 했을 때 결상관계가 \eqref{eq3} 식으로 주어지는 것을 검증하라._ 기하광학에서 부호의 약속 _ 렌즈에서의 빛의 굴절 _ 가우스 렌즈공식 _ 두 렌즈의 조합 _ 광선의 진행 _ 물체초점거리 _ 후방초점거리 _ 광선의 행동 _ 전방초점거리 _ 얇은 렌즈 _ 상초점거리 _ 근축광선 _ 볼록렌즈 _ 구면파 _ 마디점 _ 굴절률 _ 광심 _ 광축
렌즈의 결상
렌즈의 결상 얇은 렌즈 렌즈의 두께가 그 반경에 비하여 얇아서 두께가 주는 효과를 무시할 수 있고 또한 렌즈에 입사하는 광선이 렌즈의 중심축과 크게 벗어나지 않는 경우 광선이 이 렌즈에 의해 굴절되는 형태는 간단하게 작도해 낼 수 있다. 이러한 조건의 렌즈를 얇은 렌즈 (thin lens)라 하고, 이와는 반대로 렌즈의 두께를 무시할 수 없는 일반적인 렌즈를 두꺼운 렌즈 (thick lens)라고 한다. 안경이나 확대기 등은 얇은 렌즈 로 쉽게 취급할 수 있으나 고급 광학기기에 들어가는 렌즈들은 두꺼운 렌즈 로서 결상의 과정을 이해하기가 조금 어렵다. 그러나 두꺼운 렌즈 도 근사적으로는 얇은 렌즈 의 행동을 한다고 볼 수 있다. 여기서 얇은 렌즈 의 광선의 작도법을 알아보고 물체의 상 이 렌즈의 위치에 따라 어떻게 변하는지, 즉 결상의 원리 를 알아본다. sim
실제의 렌즈에 의한 결상 _ 화면 왼편에 있는 물체의 실상 이 오른쪽에 형성된다. 실제의 렌즈는 두께를 무시할 수 없고, 또한 근축광선 의 조건에서 벗어난 경우도 있기 때문에 한 점에서 나온 빛이 정확히 한 지점에 모여들지 못하여 상이 흐려진다. 그림은 오른쪽 눈의 위치에서 상을 보면 멀리 있는 물체가 바로 앞에 있는 것으로 보이는 상황이다. 왼편 붉은 원을 마우스로 옮겨서 상의 위치가 어떻게 달라지는지 살펴보자.
_ 상 _ 근축광선 _ 실상 볼록렌즈의 렌즈공식 볼록렌즈 는 양쪽이 볼록하거나 한쪽은 평평하고 다른 쪽이 볼록한 경우도 있고, 안경처럼 한쪽은 볼록하고 다른 쪽은 오목한 데 이 면의 곡률반경이 볼록한 면의 곡률반경보다 더 큰 경우도 있다. 일반적으로 볼록렌즈 는 가운데가 가장자리보다 더 두꺼운 렌즈 를 말한다. 이 볼록렌즈 의 초점거리 $f$는 왼쪽과 오른쪽의 곡률반경을 각각 $R_1$, $R_2$라 할 때 (이때 구의 중심이 경계면의 오른편에 있을 때 $+$로, 왼편에 있을 때 $-$로 한다) 다음과 같이 주어진다. 여기서 $n$은 유리의 굴절률 이다. \[ (n-1) \left( \frac{1}{R_1}- \frac{1}{R_2} \right) = \frac{1}{f} \] 초점거리 가 $f$인 볼록렌즈 에 광축 상의 점광원에서 나오는 모든 광선 은 렌즈를 통과하여 한 점에 모여들게 된다. 이때 점광원(물체)의 위치가 렌즈의 왼쪽으로 $s_o$ 떨어져 있고, 모여드는 점(상)의 위치는 렌즈의 오른쪽으로 $s_i$ 떨어져 있다고 할 때 다음의 식이 성립한다. \[ \begin{equation} \label{eq0} \frac{1}{s_o} + \frac{1}{s_i} = \frac{1}{f} \end{equation} \] 이 식은 렌즈로부터 물체와 상까지의 거리에 대한 관계로서 가우스 렌즈공식 (Gaussian lens formula)이라 한다. 경우에 따라서는 물체와 물체초점 $F_o$, 상과 상초점 $F_i$까지의 거리 $x_o$와 $x_i$로 나타내는 것이 편리할 때가 있다. \[ \begin{equation} \label{eq1} x_o x_i = f^2 \end{equation} \] 여기서 $x_o$는 물체초점 $F_o$로부터 왼쪽에 있을 때에는 양의 값으로 삼고 반면에 $x_i$는 상초점 $F_i$로부터 오른쪽으로 있을 때에 양의 값으로 삼는다. 이 식은 뉴턴이 처음으로 알아내어 뉴턴의 렌즈공식 (Newton’s lens formula)이라 한다. 이 식은 $x_o$와 $x_i$의 두 거리가 서로 반비례하고, 이들의 기하평균이 $f$이라는 것을 나타낸다. 볼록렌즈 의 경우 물체가 물체초점 의 왼쪽에서 물체초점 까지 다가가면 상은 상초점 에서 오른쪽으로 무한대까지 멀어진다. 또한 이 식은 $x_o$ 및 $x_i$의 두 값의 부호가 $f$의 부호에 관계없이 서로 같다는 것을 말하고 있다. graphic [IFrame] If this content can’t be shown well, change the Internet Browser such as ‘Chrome’.
광축 위의 광원과 결상 _ 볼록렌즈 의 광축 위의 한 점에서 나와서 렌즈를 통과한 빛은 모두 렌즈 너머 광축 위의 한 점에 다시 모여들게 된다.
[질문1] \eqref{eq1} 식이 성립하는 것을 보여라. [질문2] 어떤 볼록렌즈 에서 무한대에 있던 물체가 물체초점 의 왼편 16 cm 거리로 다가오니 상은 1 cm 이동하였다. 이 렌즈의 초점거리 는 얼마일까? [질문3] \eqref{eq1} 식은 오목렌즈 나 거울 에서도 보편적으로 성립한다. 오목렌즈 에서 물체가 렌즈 왼쪽에 있는 실물체의 경우 상은 허상 으로서 상초점 과 렌즈 사이에 위치하는 것을 보여라._ 두꺼운 렌즈 _ 물체초점 _ 초점거리 _ 상초점 _ 굴절률 _ 허상 _ 광축 _ 거울 _ 광선 광심 렌즈의 중심 역할을 하는 지점이다. 주어진 렌즈에서 한 점으로 향하는 모든 광선이 그 진로가 꺾이지 않는 특정한 지점이 있는 데 이를 렌즈의 광심 (optical center)이라 한다. 다음 그림을 보자. 편의상 양쪽 볼록렌즈 를 가정하고, 렌즈의 입사면 의 어떤 한 점 $A_1$을 선택하자. 이에 접하는 평면(그림에서는 접선)과 평행한 면을 렌즈의 출사면에 접하는 것 중에서 찾는다. 그림에서는 점 $A_2$에 접하는 평면이 될 것이다. $A_1$과 $A_2$을 이은 선이 광축 과 만나는 지점 $O$가 광심 으로 이 지점은 $A_1$의 선택에 관계없이 한 점으로 정해진다. 그림에서 붉은 색으로 나타낸 광선은 입사한 방향과 같은 방향으로 진행을 하게 되는 것을 알 수 있다. graphic [IFrame] If this content can’t be shown well, change the Internet Browser such as ‘Chrome’.
광심 _ $A_1$으로 진입한 광선 중에서 $O$를 통과한 것은 $A_2$를 통과한 후 진행방향이 입사한 방향에서 변하지 않은 채로 나아간다. 그림에서 $A_1OC_1$, $A_2OC_2$의 두 삼각형은 서로 닮은꼴이고 따라서 $O$는 $C_2$와 $C_1$을 각각의 반경 $R_2$와 $R_1$의 비율로 내분한 곳이 된다. 이 점은 렌즈에서 고유한 지점으로 광심 이라 한다.
렌즈를 통과한 광선의 진행 방향은 입사한 광선의 진행 방향에서 약간 이동하게 되나 얇은 렌즈 의 경우 이를 무시할 수 있다. 얇고 양면이 모두 볼록하거나 오목한 볼록렌즈 와 오목렌즈 의 경우 이 광심 은 렌즈와 광축 이 만나는 지점에 광심 이 있지만 초승달 같은 렌즈는 이 광심 이 렌즈로부터 벗어나 있기도 하다. 광심 은 렌즈의 상을 작도하는 데 초점과 함께 중요한 기능을 한다. 이에 대해서는 계속되는 내용에서 자세히 알아본다.
[질문1] 양쪽이 오목한 오목렌즈 와 오목볼록으로 된 볼록렌즈 , 오목볼록으로 된 오목렌즈 각각에 대해 광심 의 위치를 작도로서 정해보라. 렌즈의 바깥에 광심 이 존재하는 경우는 어떤 경우인가? 이를 어떻게 해석해야 할까? [질문2] $R_1 = 100~\text{cm}$와 $R_2 = -50~\text{cm}$이고, 중심에서의 두께가 $2~\text{cm}$인 볼록렌즈 가 유리($n=1.5$) 로 만들어져 있다. 이 렌즈의 초점거리 는 얼마인가? 또한 이 렌즈의 광심 의 위치를 정하여 이 지점을 렌즈의 모양을 그려서 표시하라._ 광선의 진행 _ 초점거리 _ 입사면 _ 광축
Copyright ⓒ 1999~ physica.gnu.ac.kr All rights reserved
렌즈 공식 유도_Derivation of the lens formula_Thin lens_Power notation
반응형
▷Derivation of the lens formula◁
-렌즈 공식 유도-
이번 글은 Thin lens에 대한, 렌즈 공식과 렌즈 제작자 공식(lens makers’ formula), 2가지에 관하여 알아볼 것이다.
가우시안 공식(Gaussian formula)과 Conjugate 관계를 알고 있다는 가정하에 접근하도록 하겠다.
혹시 이부분에 대한 이해가 부족하다면 먼저 다음 내용을 확인하면 좋을 것 같다.
↓↓
2020/06/02 – [꿀나리의 광학 이야기 ★] – 가우시안 공식_배율_Gaussian Formula_Magnification_Conjugate points and planes
< lens formula >
이전에 가우시안 공식에 대하여 포스팅한적 있는데, 비슷한 방식으로 삼각형의 닮음을 이용하여 관계식을 유도한다.
(렌즈 양면을 모두 n=1 임을 가정하고 진행한다. )
1. △Q’TS 와 △F’TA —> \(\frac{y-y’}{s’}=\frac{y}{f’}\)
2. △QTS와△FTA —> \(\frac{y-y’}{s}=\frac{-y’}{f}\)
삼각형의 닮음에서 위 두 개의 식을 얻을 수 있다. 이 식을 합하면 다음 관계식을 얻는다.
\(\frac{y-y’}{s}+\frac{y-y’}{s’}=\frac{y}{f’}-\frac{y’}{f}\)
이때 제1초점과 제2초점이 같은 경우, 즉 symmetry 한 경우 다음과 같이 가우시안 형태를 얻는다.
\(f=f’\) ——–> \(\frac{1}{s}+\frac{1}{s’}=\frac{1}{f}\) : Gaussian form
그리고 다른 삼각형에서 또 다른 식을 얻을 수 있다.
△TAF’와△F’M’Q, △QMF와△FAS —> \(\frac{y}{x}=-\frac{y’}{f}\) 와 \(\frac{-y’}{x’}=\frac{y}{f}\)
관계를 얻을 수 있고, 최종적으로 이들을 정리하여
굴절률에 대한 정보가 없을 경우에 활용할 수 있는 다음의 식을 얻을 수 있다.
\(xx’=f^{2}\) : Newtonian form
그리고 lens의 양면에 있는 매질이 다를 경우 \(xx’=ff’\) 로 쓰인다.
( 제1표면 부분의 매질과 제2표면 부분의 매질이 다를 경우를 의미한다. )
-삼각형의 닮음비가 잘 안 보일 때 참고하도록 하자.-
물체와 이미지 크기의 비율인 배율(Magnification)은 다음과 같이 구할 수 있다.
배율(Magnification) : \(m=\frac{y’}{y}=-\frac{f}{x}=-\frac{x’}{f}\)
< Lens makers' formula >
지금까지 제1표면과 제2표면이 같다는 가정하에 진행하였는데, 이번에는 이 두 부분의 다름을 고려하여
렌즈를 제작할 경우에 대한 렌즈 제작자 공식에 관한 내용이다.
방법은 똑같지만 문자와 영역에 대한 구분이 헷갈리면 식을 도출하다가 길을 잃게 될 수 있음에 유의하자.
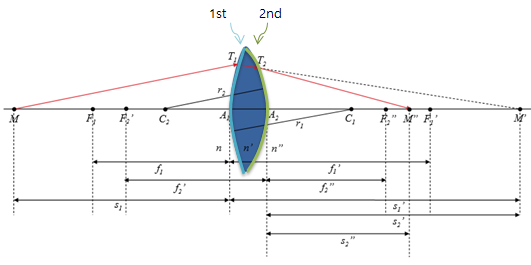
* \(A_{1}=A_{2}=A\) : 근사적으로 같다고 가정한다. *
1. 1st 표면에 MT1이 입사된다. T1은 1st표면에서 굴절된 후, M의 conjugate point M’으로 향한다. ( 빨간색 광선을 실제 빛이 진행하는 경로이며, 지금 고려하는 부분은 2nd를 고려하지 않은 1st 표면에서 굴절된 광선임을 유의하자.)
그러면 1st표면에 대한 빛은 single spherical surface에 해당하므로 (단일 구표면)
가우시안 공식을 적용하여 다음의 식을 얻을 수 있다.
㉠ : \(\frac {n}{s_{1}}+\frac {n’}{s_{1}’}=\frac {n’-n}{r_{1}}\) : Gaussian equation
2. 이제 2nd 표면을 기준으로 보았을 때, T2에서 굴절된 빛이 M”으로 향한다. 이 때, 2nd 표면에 대해서
object distance로써 \(s_{2}’\), Image distance로써 \(s_{2}”\)을 갖는다.
이 부분이 이해가 안 되거나 헷갈릴 수 있다. 조금 더 내용을 덧붙이자면,
1번에서 진행하면서 T1의 빛의 M’으로 향하였는데, 2nd 표면을 기준으로 고려하였을 때,
T2입장에서는 T1의 conjugate point M’가 Object 역할을 하면서,
2nd 기준점 A2와 M’ 사이의 거리인 \(s_{2}’\)을 object distance로 보게 된 것이다.
( 즉 T1의 Image point가 T2의 Object point가 된 것이다. )
Image point에 대한 부분은 T2에 의한 것이기 때문에 \(s_{2}”\)가 되는 것은 이해하기 어렵지 않다.
( 2nd 입장에서 보면 된다. )
그래서 2nd에서 T2의 광선에도 가우시안 공식을 적용하면 다음을 얻을 수 있다.
㉡ : \(\frac{n’}{s_{2}’}+\frac{n”}{s_{2}”}=\frac{n”-n’}{r_{2}}\) : Gaussian equation
앞서 가정한 \(A_{1}=A_{2}=A\)에 의해 렌즈 두께는 아주 얇아서 (Thin lens) Object와 Image distance를 근사적으로 같다고 할 수 있다.
㉢ : \(s_{1}’ \approx -s_{2}’\) : Image가 Object가 되었기 때문에 (-) 부호가 붙었다.
㉠,㉡의 식을 합하면 1st와 2nd에서 진행하는 빛에 관한 식을 얻는다.
\(\frac{n}{s_{1}}+\frac{n’}{s_{1}’}=\frac{n’-n}{r_{1}}\) + \(\frac{n’}{s_{2}’}+\frac{n”}{s_{2}”}=\frac{n”-n’}{r_{2}}\)
위 식을 ㉢에 의해 정리하면 다음 관계를 얻는다.
\(\frac{n}{s_{1}}+\frac{n”}{s_{2}”}=\frac{n’-n}{r_{1}}+\frac{n”-n’}{r_{2}}\) \(\approx \frac{n}{s}+\frac{n”}{s”}=\frac{n’-n}{r_{1}}+\frac{n”-n’}{r_{2}}\)
\(\frac{n}{f}=\frac{n’-n}{r_{1}}+\frac{n”-n’}{r_{2}}=\frac{n”}{f”}\) —> \(\frac{n”}{n}=\frac{f”}{f}\)
만약 렌즈가 둘러싸인 매체가 공기라면 (n=n”=1) 렌즈 제작자의 공식은 아래와 같이 정리된다.
\(\frac{1}{s}+\frac{1}{s”}=(n’-1)(\frac{1}{r_{1}}-\frac{1}{r_{2}})\) : Lens makers’ formula
간단하게 정리하면 렌즈가 공기 중에 있을 때 렌즈 제작자 공식은 다음과 같다.
\((n-1)(\frac{1}{r_{1}}-\frac{1}{r_{2}})=\frac{1}{f}=\frac{1}{f’}\) : Lens makers’ formula (n : 렌즈의 굴절률)
< The power of Thin lens >
특별한 것은 아니지만, 좀 더 편하게 사용하고자 정한 표기법이 있는데 이를 알아볼 것이다.
간단하게 문자를 치환했다고 생각하면 될 것 같다.
1. \(V=\frac{n}{s}\) 와 \(V’=\frac{n’}{s’}\) : Reduced Vergence.
2. \(P=\frac{n}{f}={n’}{f’}\) : Refracting Power.
3. \(K=\frac{1}{r}\) : Curvature of the refracting surface.
위 문자의 단위는 거리 요소가 m로 측정되었을 때 Diopter이다.
또한 가우시안 공식(Gaussian Formula)에 대해 다음과 같이 표현된다.
\(V+V’=P\) Where \(P=\frac{n’-n}{r}\) or \(P=\frac{n’-n}{K}\)
이 정보를 가지고 렌즈메이커 공식에 적용해보자.
\(V=\frac{n}{s}\) 와 \(V”=\frac{n”}{s”}\)
\(P_{1}=\frac{n’-n}{r_{1}}\) \(P_{2}=\frac{n”-n’}{r_{2}}\)
Power notation : \(V+V”=P_{1}+P_{2}\) ( \(P_{1}\) : 1st surface, \(P_{2}\) : 2nd surface )
Power of thin lens : \(P=\frac{1}{f}\) \(diopters=\frac{1}{focal length, m}\)
\(P=\frac{1}{f}=(n-1)(\frac{1}{r_{1}}-\frac{1}{r_{2}})\)
렌즈 공식 유도_Derivation of the lens formula_Thin lens_Power notation
반응형
So you have finished reading the 두꺼운 렌즈 공식 topic article, if you find this article useful, please share it. Thank you very much. See more:

