Top 49 허프만 코드 The 191 Latest Answer

You are looking for information, articles, knowledge about the topic nail salons open on sunday near me 허프만 코드 on Google, you do not find the information you need! Here are the best content compiled and compiled by the https://chewathai27.com/to team, along with other related topics such as: 허프만 코드 허프만코드 변환, 허프만 코드 파이썬, 허프만 코드 트리, 허프만 코드 자바, 허프만 트리, 허프만 코드 사이트, 허프만 코드 백준, 허프만 코드 디코딩

허프만 압축 알고리즘 강좌 (Huffman Coding Algorithm Tutorial)

허프만 코드(Huffman code)

Article author: withhamit.tistory.com
Reviews from users: 4376 Ratings
Top rated: 3.0
Lowest rated: 1
Summary of article content: Articles about 허프만 코드(Huffman code) 허프만 코드는 데이터를 효율적으로 압축하는데 사용하는 방법으로 탐욕 알고리즘 중 하나입니다. 압축하고자 하는 문자열에서 자주 등장하는 문자는 … …
Most searched keywords: Whether you are looking for 허프만 코드(Huffman code) 허프만 코드는 데이터를 효율적으로 압축하는데 사용하는 방법으로 탐욕 알고리즘 중 하나입니다. 압축하고자 하는 문자열에서 자주 등장하는 문자는 … 허프만 코드는 데이터를 효율적으로 압축하는데 사용하는 방법으로 탐욕 알고리즘 중 하나입니다. 압축하고자 하는 문자열에서 자주 등장하는 문자는 짧은 비트로 표현하고 거의 등장하지 않는 문자는 긴 비트로..
Table of Contents:

공지사항

태그

전체 방문자

티스토리툴바

Article author: velog.io
Reviews from users: 36833 Ratings
Top rated: 3.1
Lowest rated: 1
Summary of article content: Articles about 허프만 코딩(Huffman coding) 허프만 부호화 또는 허프만 코딩(Huffman coding)은 입력 파일의 문자 빈도 수를 가지고 최소힙을 이용하여 파일을 압축하는 과정이다. …
Most searched keywords: Whether you are looking for 허프만 코딩(Huffman coding) 허프만 부호화 또는 허프만 코딩(Huffman coding)은 입력 파일의 문자 빈도 수를 가지고 최소힙을 이용하여 파일을 압축하는 과정이다.
허프만 부호화 또는 허프만 코딩(Huffman coding)은 입력 파일의 문자 빈도 수를 가지고 최소힙을 이용하여 파일을 압축하는 과정이다. 허프만 코드(이진코드)는 Unix에서 파일압축에 사용되고, JPEG 이미지 파일 또는 MP3 음악 파일을 압축하기 위한 서브
Table of Contents:

알고리즘

허프만 코딩이란❓

원리

구현

복원(Decoding) 알고리즘

REF 🏷

Article author: lipcoder.tistory.com
Reviews from users: 4033 Ratings
Top rated: 4.6
Lowest rated: 1
Summary of article content: Articles about 허프만(Huffman) 트리를 이용한 텍스트 압축 개요 허프만 코딩(Huffman coding)은 텍스트 압축을 위해 널리 사용되는 방법으로, 원본 데이터에서 자주 출현하는 문자는 적은 비트의 코드로 변환 … …
Most searched keywords: Whether you are looking for 허프만(Huffman) 트리를 이용한 텍스트 압축 개요 허프만 코딩(Huffman coding)은 텍스트 압축을 위해 널리 사용되는 방법으로, 원본 데이터에서 자주 출현하는 문자는 적은 비트의 코드로 변환 … 개요 허프만 코딩(Huffman coding)은 텍스트 압축을 위해 널리 사용되는 방법으로, 원본 데이터에서 자주 출현하는 문자는 적은 비트의 코드로 변환하여 표현하고 출현 빈도가 낮은 문자는 많은 비트의 코드로 변..
Table of Contents:

기록공간

허프만(Huffman) 트리를 이용한 텍스트 압축 본문

Article author: taeminator1.tistory.com
Reviews from users: 41743 Ratings
Top rated: 3.5
Lowest rated: 1
Summary of article content: Articles about 허프만 코딩 1 – 허프만 코드 구하기 허프만 코딩 1 – 허프만 코드 구하기. Taeminator1 2021. 6. 10. 19:12. 허프만 코딩(Huffman Coding)은 이전 포스팅(https://taeminator1.tistory.com/49)에서 언급한 … …
Most searched keywords: Whether you are looking for 허프만 코딩 1 – 허프만 코드 구하기 허프만 코딩 1 – 허프만 코드 구하기. Taeminator1 2021. 6. 10. 19:12. 허프만 코딩(Huffman Coding)은 이전 포스팅(https://taeminator1.tistory.com/49)에서 언급한 … 허프만 코딩(Huffman Coding)은 이전 포스팅(https://taeminator1.tistory.com/49)에서 언급한 “더 짧은 심벌 트릭(shorter-symbol trick)”의 일종이다. 더 짧은 심벌 트릭은 압축하려는 문자열에서 자주 사용되는..
Table of Contents:

태그

‘Computer Science알고리즘’ Related Articles

Article author: junstar92.tistory.com
Reviews from users: 44044 Ratings
Top rated: 3.5
Lowest rated: 1
Summary of article content: Articles about 허프만 코딩 (C++ 구현) 허프만 코드는 (최소)우선순위 큐와 이진 트리로 만들 수 있는 유일 접두어 코드를 의미합니다. 1951년 데이비드 허프만(Dav A. Huffman)이 25살 때 … …
Most searched keywords: Whether you are looking for 허프만 코딩 (C++ 구현) 허프만 코드는 (최소)우선순위 큐와 이진 트리로 만들 수 있는 유일 접두어 코드를 의미합니다. 1951년 데이비드 허프만(Dav A. Huffman)이 25살 때 … References 리얼월드 알고리즘 허프만 코딩 허프만 코드는 (최소)우선순위 큐와 이진 트리로 만들 수 있는 유일 접두어 코드를 의미합니다. 1951년 데이비드 허프만(David A. Huffman)이 25살 때 고안한 방법으로,..
Table of Contents:

허프만 코딩

인코딩 과정

디코딩

실행 결과

전체 코드

태그

공지사항

최근글

허프만 코드(Huffman code)

320×100

허프만 코드는 데이터를 효율적으로 압축하는데 사용하는 방법으로 탐욕 알고리즘 중 하나입니다.

압축하고자 하는 문자열에서 자주 등장하는 문자는 짧은 비트로 표현하고 거의 등장하지 않는 문자는 긴 비트로 표현합니다. (가변 길이 코드)

즉, 문자의 빈도수를 이용합니다.

예시를 들어 설명하겠습니다.

EX) 압축하고자 하는 문자열 : ABBCCCDDDDEEEEEFFFFFF

-> 고정 길이 코드 : A ~F. 6개의 문자를 구분하기 위해 3bit 필요. (2^2(4) < 6 < 2^3(8) 이므로 3bit가 필요하다.) -> 가변 길이 코드 : 허프만 코드를 이용해서 나온 값.
[표 1]
<압축 결과>

고정 길이 코드 : 000001001010010010011011011011100100100100100101101101101101101

가변 길이 코드 : 100010011001101101101000000000101010101111111111111

허프만 코드를 사용한 결과(가변 길이 코드)가 더 짧다는 것을 볼 수 있습니다. -> 효율적으로 압축.

이제 어떻게 허프만 코드(가변 길이 코드)를 만드는지 알아보겠습니다.

압축하고자 하는 문자열의 예시는 마찬가지로 “ABBCCCDDDDEEEEEFFFFFF”를 사용하겠습니다.

문자열이 위의 [표 1]을 만들 때와 같으므로 허프만 코드를 완성시키면 [표 1]의 가변 길이 코드가 왜 저렇게 나왔는지 알 수 있습니다.
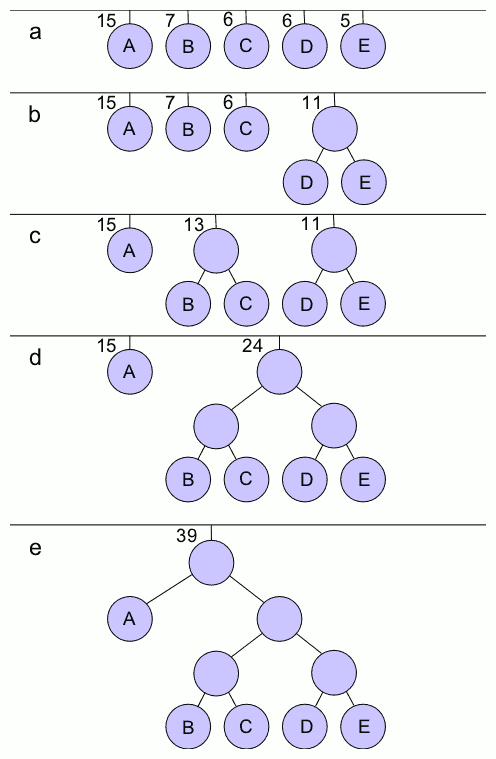
[그림 1]
우선 허프만 코드를 만들기 위해 트리를 만들어야 합니다.

우선 알파벳 별 빈도수를 저장한 노드들을 생성합니다. (그림 1)
[그림 2]
빈도수를 비교하여 가장 작은 빈도수를 가진 노드와 두 번째로 작은 빈도수를 가진 것을 찾아서 두 개의 빈도수를 합친 수로 노드를 하나 만들어 줍니다.

그리고 만들어준 노드의 왼쪽 자식에는 가장 작은 빈도 수의 노드를 연결하고 오른쪽 자식에는 두 번째로 작은 빈도수를 가진 노드를 연결합니다. (그림 2)
[그림 3]
이를 반복하여 비교할 노드가 한 개가 남을 때까지 반복합니다. (그림 3)
[그림 4]
완성한 트리 노드의 왼쪽 간선에는 0, 오른쪽 간선에는 1 가중치를 둡니다.

트리들의 단 노드가 압축하고자 하는 문자가 되며 그 문자들을 루트로부터 탐색했을 때 지난 간선들의 가중치들의 합이 허프만 코드(가변 길이 코드)가 됩니다. EX) A : 1-0-0-0 / E : 0-1

인코딩은 문자열들의 문자를 구한 허프만 코드로 치환해주면 됩니다.

디코딩도 위에 완성된 트리(그림 4)를 사용해서 하는데 인코딩된 문자열들을 앞에서부터 읽어들여 root 노드로부터 0이 나오면 왼쪽 자식으로 이동하고 1이 나오면 오른쪽 자식으로 이동하여 단 노드가 나올때까지 이를 반복합니다. 단 노드가 나온 경우 그 노드에 알맞은 알파벳을 출력한 후 다시 루트 노드로 돌아가서 반복합니다.

저는 문자 A~F로만 이루어진 문자열을 입력받아 각 문자별 허프만 코드를 출력하고 인코딩 디코딩한 결과를 출력하는 소스를 작성해 보았습니다.

이번에는 노드의 최소값 노드와 2번째 최소값 노드를 구할 때 그냥 변수를 이용하였는데 최소 힙을 이용하여 구하는 방법도 있습니다.

소스 코드 : https://gist.github.com/fpdjsns/a46dede3cbd4a05599c94fcda562a0e0 (A~F)
[실행 결과]
+

A~F만 입력받던 것을 알파벳 대문자 입력받는 것으로 바꾸어보았습니다.

소스코드 : https://gist.github.com/fpdjsns/b82d2ba881ab011f0fe001bb395fa282 (대문자)
[실행 결과]
320×100

허프만 코딩 압축 알고리즘

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121

import heapq from heapq import heappop , heappush def isLeaf ( root ) : return root . left is None and root . right is None # A 트리 노드 class Node : def __init__ ( self , ch , freq , left = None , right = None ) : self . ch = ch self . freq = freq self . left = left self . right = right # `__lt__()` 함수를 재정의하여 `Node` 클래스가 우선 순위 대기열과 함께 작동하도록 합니다. # 가장 높은 우선순위 항목이 가장 낮은 빈도를 갖도록 def __lt__ ( self , other ) : return self . freq < other . freq # 허프만 트리를 탐색하고 사전에 허프만 코드를 저장 def encode ( root , s , huffman_code ) : if root is None : return #가 리프 노드를 찾았습니다. if isLeaf ( root ) : huffman_code [ root . ch ] = s if len ( s ) > 0 else ‘1’ encode ( root . left , s + ‘0’ , huffman_code ) encode ( root . right , s + ‘1’ , huffman_code ) # 허프만 트리를 탐색하고 인코딩된 문자열을 디코딩합니다. def decode ( root , index , s ) : if root is None : return index #가 리프 노드를 찾았습니다. if isLeaf ( root ) : print ( root . ch , end = ” ) return index index = index + 1 root = root . left if s [ index ] == ‘0’ else root . right return decode ( root , index , s ) #는 허프만 트리를 구축하고 주어진 입력 텍스트를 디코딩합니다 def buildHuffmanTree ( text ) : # 기본 케이스: 빈 문자열 if len ( text ) == 0 : return #는 각 캐릭터의 출현 빈도를 계산합니다. # 사전에 저장 freq = { i : text . count ( i ) for i in set ( text ) } # Huffman 트리의 라이브 노드를 저장할 우선 순위 대기열를 만듭니다. pq = [ Node ( k , v ) for k , v in freq . items ( ) ] heapq . heapify ( pq ) # Queue에 노드가 둘 이상 있을 때까지 수행 while len ( pq ) != 1 : # 우선 순위가 가장 높은 두 노드를 제거합니다. # Queue에서 #(최저 주파수) left = heappop ( pq ) right = heappop ( pq ) #는 이 두 노드를 자식으로 사용하여 새 내부 노드를 만들고 #는 두 노드의 주파수 합과 동일한 주파수를 사용합니다. # 우선 순위 대기열에 새 노드를 추가합니다. total = left . freq + right . freq heappush ( pq , Node ( None , total , left , right ) ) # `root` 는 허프만 트리의 루트에 대한 포인터를 저장합니다. root = pq [ 0 ] #는 Huffman 트리를 탐색하고 Huffman 코드를 사전에 저장합니다. huffmanCode = { } encode ( root , ” , huffmanCode ) # 허프만 코드 인쇄 print ( ‘Huffman Codes are:’ , huffmanCode ) print ( ‘The original string is:’ , text ) # 인코딩된 문자열을 인쇄합니다. s = ” for c in text : s += huffmanCode . get ( c ) print ( ‘The encoded string is:’ , s ) print ( ‘The decoded string is:’ , end = ‘ ‘ ) if isLeaf ( root ) : # 특수 케이스: a, aa, aaa 등과 같은 입력용 while root . freq > 0 : print ( root . ch , end = ” ) root . freq = root . freq – 1 else : #는 이번에도 허프만 트리를 횡단하고, # 인코딩된 문자열 디코딩 index = – 1 while index < len ( s ) - 1 : index = decode ( root , index , s ) # Python에서 허프만 코딩 알고리즘 구현 if __name__ == '__main__' : text = 'Huffman coding is a data compression algorithm.' buildHuffmanTree ( text )

허프만 코딩(Huffman coding)

허프만 부호화 또는 허프만 코딩(Huffman coding)은 입력 파일의 문자 빈도 수를 가지고 최소힙을 이용하여 파일을 압축하는 과정이다. 허프만 코드(이진코드)는 Unix에서 파일압축에 사용되고, JPEG 이미지 파일 또는 MP3 음악 파일을 압축하기 위한 서브루틴으로도 활용된다.

허프만 코딩이란❓

처음에 허프만 코딩의 개념을 접한다면 한번에 이해하기 어려울 수 있다고 생각한다. 그래서 나는 설명하기에 좋은 비교방식을 이용해서 설명하려한다. 허프만 코딩은 앞에서 서론에서 언급했다시피 문자 빈도수를 이용해서 파일을 압축하는 과정이다. 그렇다면 기존에는 어떻게 사용하고있는데, 어떻게 얼마나 압축이 될까?

고정 길이 코드(fixed length code) vs 접두어 코드(prefix code)

고정 길이 코드는 대표적으로 아스키 코드가 있다. 아스키 코드는 항상 8bit의 길이를 가지고있다. 다루기에는 간단하지만, 저장 공간 활용에 있어서 제한이 있다. 이를 해결하기 위해서 가변 길이 코드(variable length code)가 존재한다.

가변 길이 코드 중에서도 접두어 코드는, 앞서 나온 문자가 다음에 나올 문자의 접두어가 되면 안되는 특징을 가진 코드다. 예를 들면 다음은 접두어 코드가 아닌 예다.

a : 01

b : 101

c : 010

위 코드에서 01 은 010 의 접두어이기 때문에 접두어 코드가 아니다. 반면 다음은 접두어 코드의 예다.

a : 01

b : 10

c : 111

이 접두어 코드를 아스키코드로 한다면? 총 24bit의 저장 공간을 소비한다. 반면에 압축한 상태 그대로 이진코드로 표현한다면 0110111로 7bit로 압축이 가능하게된다. 이처럼 입력 문자의 빈도수를 가지고 압축하는 것이 허프만 코딩이다.

원리

허프만 트리를 만들어서 압축을 하기위해서는 다음과 같은 원리도 수행된다.

압축할 파일을 스캔하여 각 문자의 빈도 수를 계산한다.

빈도 수를 우선순위로 최소힙 h를 구성한다.

빈도 수가 가장 작은 두 노드들을 삭제한다.

삭제한 두 노드 중에 작은 것을 왼쪽 자식노드, 큰 것을 오른쪽 자식노드로 하는 노드를 삽입

노드가 하나가 남을 때까지 반복한다.

마지막 노드가 루트 노드가 된다.

빈도 수가 높은 문자에는 짧은 이진코드(허프만 코드)를 부여하고, 빈도 수가 낮은 문자에는 긴 이진코드를 부여하여 압축 효율을 높인다.

구현

기본적으로 자료구조 Heap을 이용하기때문에, 기본적인 뼈대는 [자료구조] Heap을 참고하자. 다만, 위의 원리에서 언급한 6가지 순서에 대한 구현만 알아보자.

public class Entry { private int frequency ; private String word ; private Entry left ; private Entry right ; private String code ; public Entry ( int newFreq , String newVal , Entry l , Entry r , String newCode ) { frequency = newFreq ; word = newVal ; left = l ; right = r ; code = newCode ; } public int getFrequency ( ) { return frequency ; } public void setFrequency ( int frequency ) { this . frequency = frequency ; } public String getWord ( ) { return word ; } public void setWord ( String word ) { this . word = word ; } public Entry getLeft ( ) { return left ; } public void setLeft ( Entry left ) { this . left = left ; } public Entry getRight ( ) { return right ; } public void setRight ( Entry right ) { this . right = right ; } public String getCode ( ) { return code ; } public void setCode ( String code ) { this . code = code ; }

public class Huffman { private Entry [ ] harray ; private int size ; public Huffman ( Entry [ ] heapArray , int initialSize ) { harray = heapArray ; size = initialSize ; } private boolean greater ( int i , int j ) { return harray [ i ] . getFrequency ( ) > harray [ j ] . getFrequency ( ) ; } public Entry createTree ( ) { while ( size ( ) > 1 ) { Entry e1 = deleteMin ( ) ; Entry e2 = deleteMin ( ) ; Entry temp = new Entry ( e1 . getFrequency ( ) + e2 . getFrequency ( ) , e1 . getWord ( ) + e2 . getWord ( ) , e1 , e2 , ” ” ) ; insert ( temp ) ; } return deleteMin ( ) ; } }

복원(Decoding) 알고리즘

각 문자에 대응되는 허프만 코드는 prefix code이기 때문에 01#001#110 과 같이 구분자를 사용하지 않고 01001110 를 사용할 수 있다. 그렇다면 복원할때는 긴 비트 스트링을 어디서 끊어야할까?

기본적으로 알려진 방법으로는 첫번째 비트인 트리 상 루트노드로부터 비트가 0이면 왼쪽 1이면 오른쪽으로 타고 내려가다가 리프노드에 도달하는 순간에 리프노트가 가진 문자로 변환하고, 그 다음 비트들도 같은 방법으로 문자로 변환할 수 있다.

문자를 가지는 노드는 모두 리프노드다.

하지만 이 방법은 허프만 트리의 높이에 시간복잡도가 비례한다는 특성을 가지고 있다. 문자들의 빈도수에 따라서 적게는 O(logN) 부터 많게는 O(N)의 시간복잡도를 가진다. 따라서 최악의 경우 단 한개의 문자를 복원하는데 O(N)의 시간복잡도를 소요하는 상황이 발생할 수 있다.

REF 🏷

So you have finished reading the 허프만 코드 topic article, if you find this article useful, please share it. Thank you very much. See more: 허프만코드 변환, 허프만 코드 파이썬, 허프만 코드 트리, 허프만 코드 자바, 허프만 트리, 허프만 코드 사이트, 허프만 코드 백준, 허프만 코드 디코딩

Top 49 허프만 코드 The 191 Latest Answer

허프만 코드(Huffman code)

허프만 코딩(Huffman coding)

허프만(Huffman) 트리를 이용한 텍스트 압축

허프만 코딩 1 – 허프만 코드 구하기

허프만 코딩 (C++ 구현)

[알고리즘 정리] 허프만 코드(Huffman Code Problem)

[허프만 코드] Huffman Code의 이해 및 구현

허프만 코드(Huffman code)

허프만 코딩 압축 알고리즘

허프만 코딩(Huffman coding)

Leave a Comment Cancel reply