You are looking for information, articles, knowledge about the topic nail salons open on sunday near me 제 2 코사인 법칙 on Google, you do not find the information you need! Here are the best content compiled and compiled by the Chewathai27.com/to team, along with other related topics such as: 제 2 코사인 법칙 제1코사인법칙, 제 3 코사인법칙, 제2코사인법칙 영어로, 제 2 코사인 법칙 계산기, 제2코사인법칙 벡터 증명, 제1코사인법칙 교육과정, 사인법칙 코사인법칙, 코사인법칙 활용
기하학에서 코사인 법칙(cosine法則, 영어: law of cosines)은 삼각형의 세 변과 한 각의 코사인 사이에 성립하는 정리이다. 이에 따르면, 삼각형의 두 변의 제곱합에서 사잇각의 코사인과 그 두 변의 곱의 2배를 빼면, 남은 변의 제곱과 같아진다.
코사인 법칙 – 위키백과, 우리 모두의 백과사전
- Article author: ko.wikipedia.org
- Reviews from users: 25815
Ratings
- Top rated: 3.7
- Lowest rated: 1
- Summary of article content: Articles about 코사인 법칙 – 위키백과, 우리 모두의 백과사전 Updating …
- Most searched keywords: Whether you are looking for 코사인 법칙 – 위키백과, 우리 모두의 백과사전 Updating
- Table of Contents:
정의[편집]
역사[편집]
증명[편집]
비유클리드 기하학의 경우[편집]
같이 보기[편집]
각주[편집]
외부 링크[편집]

코사인법칙, 제2 코사인법칙 증명 – 수학방
- Article author: mathbang.net
- Reviews from users: 24328
Ratings
- Top rated: 3.4
- Lowest rated: 1
- Summary of article content: Articles about 코사인법칙, 제2 코사인법칙 증명 – 수학방 제2 코사인법칙 증명 · a = bcosC + ccosB · b = ccosA + acosC · c = acosB + bcosA. …
- Most searched keywords: Whether you are looking for 코사인법칙, 제2 코사인법칙 증명 – 수학방 제2 코사인법칙 증명 · a = bcosC + ccosB · b = ccosA + acosC · c = acosB + bcosA. 코사인법칙 두 번째 제2 코사인법칙이에요. 제2 코사인법칙은 제1 코사인법칙의 확장판이에요. 따라서 제1 코사인법칙에 대해서 알고 있어야 하고 증명도 할 줄 알아야 해요. 이 글에서는 제2 코사인법칙을 유도해..
- Table of Contents:
코사인법칙 제2 코사인법칙 증명
댓글(7개) 펼치기닫기

제2코사인법칙 공식 및 유도과정
- Article author: houseofj.tistory.com
- Reviews from users: 46288
Ratings
- Top rated: 4.9
- Lowest rated: 1
- Summary of article content: Articles about 제2코사인법칙 공식 및 유도과정 제2코사인법칙은 모든 삼각형에서 증명이 가능하다. △ABC의 꼭지점 B에서 밑변 또는 그 연장선 위에 내린 수선의 발을 D, 선분BD=h, 선분AD=x라고 … …
- Most searched keywords: Whether you are looking for 제2코사인법칙 공식 및 유도과정 제2코사인법칙은 모든 삼각형에서 증명이 가능하다. △ABC의 꼭지점 B에서 밑변 또는 그 연장선 위에 내린 수선의 발을 D, 선분BD=h, 선분AD=x라고 … 제2코사인법칙이란? 임의의 삼각형이 주어졌을 때, 제1코사인법칙과 제2코사인법칙이 성립된다. 다음과 같은 삼각형이 주어졌을 때 다음과 같은 식이 성립한다. 위의 식을 제2코사인법칙이라고 한다. 상당히..집 같은 느낌으로 편안하게 정보를 접할 수 있는 곳
- Table of Contents:
제2코사인법칙 공식 및 유도과정
티스토리툴바

제1,2코사인법칙 : 네이버 블로그
- Article author: m.blog.naver.com
- Reviews from users: 49166
Ratings
- Top rated: 4.8
- Lowest rated: 1
- Summary of article content: Articles about 제1,2코사인법칙 : 네이버 블로그 제1,2코사인법칙 · 1.각 A가 예각일때,. 삼각형 ABC에서 C에서 내린 수선의 발을 H라고 할때 H의 위치에 따라 왼쪽의 경우는 선분BH=c-bcosx, 오른쪽의 … …
- Most searched keywords: Whether you are looking for 제1,2코사인법칙 : 네이버 블로그 제1,2코사인법칙 · 1.각 A가 예각일때,. 삼각형 ABC에서 C에서 내린 수선의 발을 H라고 할때 H의 위치에 따라 왼쪽의 경우는 선분BH=c-bcosx, 오른쪽의 …
- Table of Contents:
카테고리 이동
평범한 수덕의 블로그
이 블로그
잡지식
카테고리 글
카테고리
이 블로그
잡지식
카테고리 글
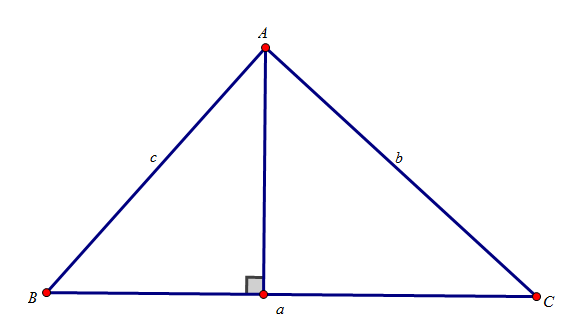
삼각함수 제 2코사인 법칙 총정리(공식, 예제풀이)
- Article author: alive-earth.com
- Reviews from users: 44823
Ratings
- Top rated: 4.0
- Lowest rated: 1
- Summary of article content: Articles about 삼각함수 제 2코사인 법칙 총정리(공식, 예제풀이) 코사인 제 2법칙은 다음과 같습니다. 어려워보이지만 사실은 간단한데요. 우리가 구하고자하는 변의 제곱은 다른 변의 제곱의 합에서 다른 두변의 곱에 2 … …
- Most searched keywords: Whether you are looking for 삼각함수 제 2코사인 법칙 총정리(공식, 예제풀이) 코사인 제 2법칙은 다음과 같습니다. 어려워보이지만 사실은 간단한데요. 우리가 구하고자하는 변의 제곱은 다른 변의 제곱의 합에서 다른 두변의 곱에 2 … 안녕하세요. 훈릴스입니다. 오늘은 삼각함수의 공식 중 제 2 코사인 법칙에 대해 알아보는 시간을 가져보고자 합니다. 요즘들어 삼각함수와 관련된 포스팅을 많이하고 있는데요. 정말 해도해도 끝이없는 것이 수험..
- Table of Contents:
태그
관련글
댓글0
공지사항
최근댓글
티스토리툴바
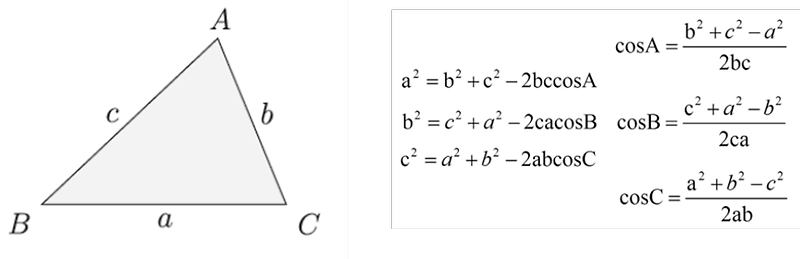
사인법칙, 제1코사인법칙, 제2코사인법칙 – MATH FACTORY
- Article author: www.mathfactory.net
- Reviews from users: 39182
Ratings
- Top rated: 4.8
- Lowest rated: 1
- Summary of article content: Articles about 사인법칙, 제1코사인법칙, 제2코사인법칙 – MATH FACTORY 사인법칙 사인법칙은 삼각형에서 사인 값과 변의 길이 사이의 관계를 나타낸 공식입니다. 원에 내접하는 삼각형을 이용하여 공식을 유도합니다. …
- Most searched keywords: Whether you are looking for 사인법칙, 제1코사인법칙, 제2코사인법칙 – MATH FACTORY 사인법칙 사인법칙은 삼각형에서 사인 값과 변의 길이 사이의 관계를 나타낸 공식입니다. 원에 내접하는 삼각형을 이용하여 공식을 유도합니다. 사인법칙 사인법칙은 삼각형에서 사인 값과 변의 길이 사이의 관계를 나타낸 공식입니다. 원에 내접하는 삼각형을 이용하여 공식을 유도합니다. 다음과 같이 반지름의 길이가 $ \mathrm{R} $인 원 위에 삼각형 $ \mathrm{ABC} $를 그리고, 변 $ \mathrm{BC} $를 $ a $라고 하겠습니다. 점 $ \mathrm{B} $를 지나는 지름을 긋고 그 지름의 반대편 끝을 $ \mathrm{A’} $이라고 하면, 삼각형 […]
- Table of Contents:
Menu
사인법칙 제1코사인법칙 제2코사인법칙
수학 공식 – 2015년 개정

코사인법칙의 다양한 증명(코사인법칙 증명) – JW MATHidea
- Article author: jwmath.tistory.com
- Reviews from users: 41524
Ratings
- Top rated: 4.9
- Lowest rated: 1
- Summary of article content: Articles about 코사인법칙의 다양한 증명(코사인법칙 증명) – JW MATHidea 2. 제이 코사인 법칙 증명. 삼각형 ABC에서 제일 코사인법칙에 의해. 이므로 각 식의 양변에 차례로 a, b, … [수학Flash] – 사인법칙, 코사인법칙 … …
- Most searched keywords: Whether you are looking for 코사인법칙의 다양한 증명(코사인법칙 증명) – JW MATHidea 2. 제이 코사인 법칙 증명. 삼각형 ABC에서 제일 코사인법칙에 의해. 이므로 각 식의 양변에 차례로 a, b, … [수학Flash] – 사인법칙, 코사인법칙 … 코사인 법칙 코사인법칙을 증명해 보자. 삼각형 ABC에서 삼각형 ABC의 꼭짓점 A에서 변 BC 또는 그 연장선에 내린 수선의 발을 H라고 할 때, ∠C의 크기에 따라 다음의 세 가지 경우로 나누어 생각할 수 있다…
- Table of Contents:

코사인 제 2법칙 증명
- Article author: color-change.tistory.com
- Reviews from users: 33090
Ratings
- Top rated: 5.0
- Lowest rated: 1
- Summary of article content: Articles about 코사인 제 2법칙 증명 식의 패턴을 잘 파악해야 합니다. 세 식 모두 우리가 관심있어하는 특정 변이 좌변에 있고, 우변에는 그 변을 제외한 나머지 두 변과 그 변에 대응하는 … …
- Most searched keywords: Whether you are looking for 코사인 제 2법칙 증명 식의 패턴을 잘 파악해야 합니다. 세 식 모두 우리가 관심있어하는 특정 변이 좌변에 있고, 우변에는 그 변을 제외한 나머지 두 변과 그 변에 대응하는 … 안녕하세요. 컬러체인지 입니다. 이 포스팅은 수1 이전 과목 중 가장 중요하다고 손꼽히는 코사인 제 2법칙 의 증명 및 식의 의미 이해에 관한 글입니다. 코사인 제 2법칙이란? 위와같은 삼..
- Table of Contents:
고정 헤더 영역
메뉴 레이어
검색 레이어
상세 컨텐츠
코사인 제 2법칙이란
코사인 제 2법칙 증명
태그
추가 정보
페이징

See more articles in the same category here: Top 673 tips update new.
위키백과, 우리 모두의 백과사전
기하학에서 코사인 법칙(cosine法則, 영어: law of cosines)은 삼각형의 세 변과 한 각의 코사인 사이에 성립하는 정리이다. 이에 따르면, 삼각형의 두 변의 제곱합에서 사잇각의 코사인과 그 두 변의 곱의 2배를 빼면, 남은 변의 제곱과 같아진다. 삼각형의 두 변의 직각 삼각형에 대한 피타고라스의 정리에 대한 일반화이다. 코사인 법칙은 삼각형의 두 변과 그 사잇각을 알 때 남은 한 변을 구하거나, 세 변을 알 때 세 각을 구하는 데 사용될 수 있다.
정의 [ 편집 ]
A , B , C {\displaystyle A,B,C} a , b , c {\displaystyle a,b,c} 삼각형의 세 각및 이들이 마주하는 변
삼각형 A B C {\displaystyle ABC} 의 세 각 A , B , C {\displaystyle A,B,C} 가 마주하는 변이 각각 a , b , c {\displaystyle a,b,c} 라고 하면, 다음이 성립한다.
c 2 = a 2 + b 2 − 2 a b cos C {\displaystyle c^{2}=a^{2}+b^{2}-2ab\cos C}
여기서 cos {\displaystyle \cos } 은 삼각 함수의 하나인 코사인이다. 이를 코사인 법칙이라고 한다.[1]
코사인 법칙을 통해 삼각형의 두 변과 그 사잇각으로부터 제3의 변을 구할 수 있다. 또한, 삼각형의 세 변으로부터 세 각을 다음과 같이 구할 수 있다.[1]
cos C = a 2 + b 2 − c 2 2 a b {\displaystyle \cos C={\frac {a^{2}+b^{2}-c^{2}}{2ab}}}
코사인 법칙에서 C {\displaystyle C} 가 직각일 경우, cos C = 0 {\displaystyle \cos C=0} 이므로, 다음과 같은 피타고라스의 정리를 얻는다.[1]
c 2 = a 2 + b 2 {\displaystyle c^{2}=a^{2}+b^{2}}
역사 [ 편집 ]
유클리드의 《원론》 2권 명제12 및 명제 13은 코사인 법칙과 동치인 명제를 서술한다.
명제12
둔각 삼각형에서, 둔각을 마주하는 변 위의 정사각형은 둔각을 이루는 변들 위의 정사각형들(의 합)보다 수직 (직선)이 내려진 둔각의 변, 그리고 둔각을 향한 수직 (직선)에 의해 (삼각형의) 밖에서 절단된 (직선)이 이루는 (직사각형)의 두 배만큼 많다.
Proposition 12†
In obtuse-angled triangles, the square on the side subtending the obtuse angle is greater than the (sum of the) squares on the sides containing the obtuse angle by twice the (rectangle) contained by one of the sides around the obtuse angle, to which a perpendicular (straight-line) falls, and the (straight-line) cut off outside (the triangle) by the perpendicular (straight-line) towards the obtuse angle. — [2]
명제13
예각 삼각형에서, 예각을 마주하는 변 위의 정사각형은 예각을 이루는 변들 위의 정사각형들(의 합)보다 수직 (직선)이 내려진 예각의 변, 그리고 예각을 향하는 수직 (직선)에 의해 (삼각형의) 안에서 절단된 (직선)이 이루는 (직사각형)의 두 배만큼 적다.
Proposition 13†
In acute-angled triangles, the square on the side subtending the acute angle is less than the (sum of the) squares on the sides containing the acute angle by twice the (rectangle) contained by one of the sides around the acute angle, to which a perpendicular (straight-line) falls, and the (straight-line) cut off inside (the triangle) by the perpendicular (straight-line) towards the acute angle. — [2]
레기오몬타누스는 1462~3년에 작성한 《삼각형에 대하여》(라틴어: De Triangulis)에서 (제1) 구면 코사인 법칙을 제시하였다.[3] 프랑수아 비에트는 1579년 저서 《표준 수학》(라틴어: Canon Mathematicus)에서 제2 구면 코사인 법칙을 제시하였다.[3]
증명 [ 편집 ]
유클리드의 《원론》에서의 증명 [ 편집 ]
그림과 같이, C {\displaystyle C} 를 둔각으로 하는 둔각 삼각형 A B C {\displaystyle ABC} 의 높이선 B H {\displaystyle BH} 를 긋자. 그렇다면, A B H {\displaystyle ABH} 는 H {\displaystyle H} 를 직각으로 하는 직각 삼각형이므로, 피타고라스의 정리에 따라 다음이 성립한다.
A B 2 = A H 2 + B H 2 {\displaystyle AB^{2}=AH^{2}+BH^{2}}
또한, A H = A C + C H {\displaystyle AH=AC+CH} 이므로, 다음이 성립한다.
A B 2 = ( A C + C H ) 2 + B H 2 = A C 2 + 2 ( A C ) ( C H ) + C H 2 + B H 2 {\displaystyle AB^{2}=(AC+CH)^{2}+BH^{2}=AC^{2}+2(AC)(CH)+CH^{2}+BH^{2}}
마지막 두 항을 직각 삼각형 B C H {\displaystyle BCH} 에 대한 피타고라스의 정리를 통해 정리하면 다음을 얻는다.
A B 2 = A C 2 + 2 ( A C ) ( C H ) + B C 2 {\displaystyle AB^{2}=AC^{2}+2(AC)(CH)+BC^{2}}
이로써 유클리드의 《원론》 2권 명제12가 증명된다. 코사인의 정의에 따라
cos C = − cos ( π − C ) = − C H B C {\displaystyle \cos C=-\cos(\pi -C)=-{\frac {CH}{BC}}}
이므로, 코사인 법칙
A B 2 = A C 2 + B C 2 − 2 ( A C ) ( B C ) cos C {\displaystyle AB^{2}=AC^{2}+BC^{2}-2(AC)(BC)\cos C}
이 C {\displaystyle C} 가 둔각일 경우 성립함을 알 수 있다.[2] C {\displaystyle C} 가 예각일 경우의 증명은 이와 비슷하다.
삼각법을 통한 증명 [ 편집 ]
코사인 법칙의 삼각법 을 통한 증명
삼각형의 세 변을 각각 높이선으로 안에서 또는 밖에서 나누면 다음을 얻는다.[4]
a = b cos C + c cos B {\displaystyle a=b\cos C+c\cos B} b = a cos C + c cos A {\displaystyle b=a\cos C+c\cos A} c = a cos B + b cos A {\displaystyle c=a\cos B+b\cos A}
세 등식의 양변에 각각 a , b , c {\displaystyle a,b,c} 를 곱하면 다음을 얻는다.
a 2 = a b cos C + a c cos B {\displaystyle a^{2}=ab\cos C+ac\cos B} b 2 = a b cos C + b c cos A {\displaystyle b^{2}=ab\cos C+bc\cos A} c 2 = a c cos B + b c cos A {\displaystyle c^{2}=ac\cos B+bc\cos A}
이제 첫째 등식에 둘째 등식을 더한 뒤 셋째 등식을 빼면 다음을 얻는다.
a 2 + b 2 − c 2 = 2 a b cos C {\displaystyle a^{2}+b^{2}-c^{2}=2ab\cos C}
이로써 코사인 법칙이 증명된다.
벡터와 스칼라곱을 사용한 증명 [ 편집 ]
다음과 같은 세 벡터를 정의하자.
a = C B → , b = C A → , c = A B → = a − b {\displaystyle \mathbf {a} ={\overrightarrow {CB}},\;\mathbf {b} ={\overrightarrow {CA}},\;\mathbf {c} ={\overrightarrow {AB}}=\mathbf {a} -\mathbf {b} }
그렇다면, 벡터 a , b , c {\displaystyle \mathbf {a} ,\mathbf {b} ,\mathbf {c} } 의 길이는 각각 a , b , c {\displaystyle a,b,c} 이며, 벡터 a {\displaystyle \mathbf {a} } 와 b {\displaystyle \mathbf {b} } 사이의 각도는 C {\displaystyle C} 이다. 따라서, 코사인 법칙을 벡터의 스칼라곱의 성질에 따라 다음과 같이 간단히 증명할 수 있다.[5]
c 2 = c ⋅ c = ( a − b ) ⋅ ( a − b ) = a ⋅ a + b ⋅ b − 2 a ⋅ b = a 2 + b 2 − 2 a b cos C {\displaystyle {\begin{aligned}c^{2}&=\mathbf {c} \cdot \mathbf {c} \\&=(\mathbf {a} -\mathbf {b} )\cdot (\mathbf {a} -\mathbf {b} )\\&=\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2\mathbf {a} \cdot \mathbf {b} \\&=a^{2}+b^{2}-2ab\cos C\end{aligned}}}
비유클리드 기하학의 경우 [ 편집 ]
구면 코사인 법칙 [ 편집 ]
A , B , C {\displaystyle A,B,C} a , b , c {\displaystyle a,b,c} 구면 삼각형의 세 각와 이들이 마주하는 세 변
단위 구면 위의 구면 삼각형 A B C {\displaystyle ABC} 의 세 각 A , B , C {\displaystyle A,B,C} 가 마주하는 세 변이 각각 a , b , c {\displaystyle a,b,c} 라고 하면, 다음이 성립한다.
cos c = cos a cos b + sin a sin b cos C {\displaystyle \cos c=\cos a\cos b+\sin a\sin b\cos C}
여기서 cos , sin {\displaystyle \cos ,\sin } 은 각각 코사인, 사인이다. 이를 (제1) 구면 코사인 법칙(第一球面cosine法則, 영어: (first) spherical law of cosines)이라고 한다. 이에 대한 쌍대 명제는 다음과 같다.
cos C = − cos A cos B + sin A sin B cos c {\displaystyle \cos C=-\cos A\cos B+\sin A\sin B\cos c}
이를 제2 구면 코사인 법칙(第二球面cosine法則, 영어: second spherical law of cosines)이라고 한다.
이 둘은 각각 다음과 같이 쓸 수 있다.
cos C = cos c − cos a cos b sin a sin b {\displaystyle \cos C={\frac {\cos c-\cos a\cos b}{\sin a\sin b}}} cos c = cos C + cos A cos B sin A sin B {\displaystyle \cos c={\frac {\cos C+\cos A\cos B}{\sin A\sin B}}}
제1 구면 코사인 법칙의 증명 (법벡터 사용) [ 편집 ]
다음과 같은 벡터들을 정의하자.
u = O A → − ( O C → ⋅ O A → ) O C → | O A → − ( O C → ⋅ O A → ) O C → | , v = O B → − ( O C → ⋅ O B → ) O C → | O B → − ( O C → ⋅ O B → ) O C → | {\displaystyle \mathbf {u} ={\frac {{\overrightarrow {OA}}-({\overrightarrow {OC}}\cdot {\overrightarrow {OA}}){\overrightarrow {OC}}}{|{\overrightarrow {OA}}-({\overrightarrow {OC}}\cdot {\overrightarrow {OA}}){\overrightarrow {OC}}|}},\;\mathbf {v} ={\frac {{\overrightarrow {OB}}-({\overrightarrow {OC}}\cdot {\overrightarrow {OB}}){\overrightarrow {OC}}}{|{\overrightarrow {OB}}-({\overrightarrow {OC}}\cdot {\overrightarrow {OB}}){\overrightarrow {OC}}|}}}
즉, u , v {\displaystyle \mathbf {u} ,\mathbf {v} } 는 각각 C {\displaystyle C} 에서 A , B {\displaystyle A,B} 를 향하는 구면의 단위 접벡터이다. 그렇다면, u , v {\displaystyle \mathbf {u} ,\mathbf {v} } 사이의 각도는 C {\displaystyle C} 이다. 또한, { O C → , u } , { O C → , v } {\displaystyle \{{\overrightarrow {OC}},\mathbf {u} \},\{{\overrightarrow {OC}},\mathbf {v} \}} 는 각각 평면 O A C , O A B {\displaystyle OAC,OAB} 의 정규 직교 기저를 이루므로, O A → , O B → {\displaystyle {\overrightarrow {OA}},{\overrightarrow {OB}}} 를 각각 다음과 같이 분해할 수 있다.
O A → = cos a ⋅ O C → + sin a ⋅ u {\displaystyle {\overrightarrow {OA}}=\cos a\cdot {\overrightarrow {OC}}+\sin a\cdot \mathbf {u} } O B → = cos b ⋅ O C → + sin b ⋅ v {\displaystyle {\overrightarrow {OB}}=\cos b\cdot {\overrightarrow {OC}}+\sin b\cdot \mathbf {v} }
따라서, 다음이 성립한다.
cos c = O A → ⋅ O B → = ( cos a ⋅ O C → + sin a ⋅ u ) ⋅ ( cos b ⋅ O C → + sin b ⋅ v ) = cos a cos b + sin a sin b cos C {\displaystyle {\begin{aligned}\cos c&={\overrightarrow {OA}}\cdot {\overrightarrow {OB}}\\&=(\cos a\cdot {\overrightarrow {OC}}+\sin a\cdot \mathbf {u} )\cdot (\cos b\cdot {\overrightarrow {OC}}+\sin b\cdot \mathbf {v} )\\&=\cos a\cos b+\sin a\sin b\cos C\end{aligned}}}
제1 구면 코사인 법칙의 증명 (비네-코시 항등식 사용) [ 편집 ]
단위 구면의 중심을 O {\displaystyle O} 라고 하자. 또한, 다음과 같은 세 벡터를 정의하자.
a = O A → , b = O B → , c = O C → {\displaystyle \mathbf {a} ={\overrightarrow {OA}},\;\mathbf {b} ={\overrightarrow {OB}},\;\mathbf {c} ={\overrightarrow {OC}}}
그렇다면, a , b , c {\displaystyle \mathbf {a} ,\mathbf {b} ,\mathbf {c} } 의 길이는 모두 1이며, a , b {\displaystyle \mathbf {a} ,\mathbf {b} } 사이의 각도는 c {\displaystyle c} 이며, a , c {\displaystyle \mathbf {a} ,\mathbf {c} } 사이의 각도는 b {\displaystyle b} 이며, b , c {\displaystyle \mathbf {b} ,\mathbf {c} } 사이의 각도는 a {\displaystyle a} 이다. 따라서, 벡터곱 a × b {\displaystyle \mathbf {a} \times \mathbf {b} } , a × c {\displaystyle \mathbf {a} \times \mathbf {c} } , b × c {\displaystyle \mathbf {b} \times \mathbf {c} } 의 길이는 각각 sin c {\displaystyle \sin c} , sin b {\displaystyle \sin b} , sin a {\displaystyle \sin a} 이다. 또한, a × b {\displaystyle \mathbf {a} \times \mathbf {b} } 와 a × c {\displaystyle \mathbf {a} \times \mathbf {c} } 사이의 각도는 A {\displaystyle A} 이며, b × a {\displaystyle \mathbf {b} \times \mathbf {a} } 와 b × c {\displaystyle \mathbf {b} \times \mathbf {c} } 사이의 각도는 B {\displaystyle B} 이며, c × a {\displaystyle \mathbf {c} \times \mathbf {a} } 와 c × b {\displaystyle \mathbf {c} \times \mathbf {b} } 사이의 각도는 C {\displaystyle C} 이다. 이제, 비네-코시 항등식에 따라 다음이 성립함에 주의하자.
( c × b ) ⋅ ( c × a ) = ( c ⋅ c ) ( a ⋅ b ) − ( c ⋅ b ) ( c ⋅ a ) {\displaystyle (\mathbf {c} \times \mathbf {b} )\cdot (\mathbf {c} \times \mathbf {a} )=(\mathbf {c} \cdot \mathbf {c} )(\mathbf {a} \cdot \mathbf {b} )-(\mathbf {c} \cdot \mathbf {b} )(\mathbf {c} \cdot \mathbf {a} )}
여기에 위의 결과들을 대입하면 다음을 얻는다.
sin a sin b cos C = cos c − cos a cos b {\displaystyle \sin a\sin b\cos C=\cos c-\cos a\cos b}
이로써 제1 구면 코사인 법칙이 증명된다.
제2 구면 코사인 법칙의 증명 [ 편집 ]
구면 삼각형 A B C {\displaystyle ABC} 의 극삼각형을 A ′ B ′ C ′ {\displaystyle A’B’C’} 라고 하자. 그렇다면, 다음이 성립한다.
a ′ = π − A , b ′ = π − B , c ′ = π − C {\displaystyle a’=\pi -A,\;b’=\pi -B,\;c’=\pi -C} A ′ = π − a , B ′ = π − b , C ′ = π − c {\displaystyle A’=\pi -a,\;B’=\pi -b,\;C’=\pi -c}
따라서 제1 구면 코사인 법칙을 극삼각형 A ′ B ′ C ′ {\displaystyle A’B’C’} 에 적용하면, 구면 삼각형 A B C {\displaystyle ABC} 에 대한 제2 구면 코사인 법칙을 얻는다.
쌍곡 코사인 법칙 [ 편집 ]
가우스 곡률 -1의 쌍곡면 위의 쌍곡 삼각형 A B C {\displaystyle ABC} 의 세 각 A , B , C {\displaystyle A,B,C} 이 마주하는 변이 각각 a , b , c {\displaystyle a,b,c} 라고 하면, 다음이 성립한다.
cosh c = cosh a cosh b − sinh a sinh b cos C {\displaystyle \cosh c=\cosh a\cosh b-\sinh a\sinh b\cos C}
여기서 cosh , sinh {\displaystyle \cosh ,\sinh } 는 각각 쌍곡 코사인, 쌍곡 사인이다. 이를 (제1) 쌍곡 코사인 법칙((第一)雙曲cosine法則, 영어: (first) hyperbolic law of cosines)이라고 한다. 마찬가지로, 다음이 성립한다.
cos C = − cos A cos B + sin A sin B cosh c {\displaystyle \cos C=-\cos A\cos B+\sin A\sin B\cosh c}
이를 제2 쌍곡 코사인 법칙(第二雙曲cosine法則, 영어: second hyperbolic law of cosines)이라고 한다.
이 두 법칙은 각각 다음과 같이 다시 쓸 수 있다.[6]
cos C = cosh a cosh b − cosh c sinh a sinh b {\displaystyle \cos C={\frac {\cosh a\cosh b-\cosh c}{\sinh a\sinh b}}} cosh c = cos A cos B + cos C sin A sin B {\displaystyle \cosh c={\frac {\cos A\cos B+\cos C}{\sin A\sin B}}}
특히, C {\displaystyle C} 가 직각일 경우의 제1 쌍곡 코사인 법칙은 쌍곡 피타고라스 정리가 된다.[6]
cosh c = cosh a cosh b {\displaystyle \cosh c=\cosh a\cosh b}
제1 쌍곡 코사인 법칙의 증명 [ 편집 ]
복소 평면 C {\displaystyle \mathbb {C} } 위의 열린 단위 원판 D ⊆ C {\displaystyle D\subseteq \mathbb {C} } 위에서 푸앵카레 원판 모형을 취하자. 쌍곡 삼각형 z 1 , z 2 , z 3 {\displaystyle z_{1},z_{2},z_{3}} 의 세 각의 크기를 A , B , C {\displaystyle A,B,C} , 세 변의 길이를 a , b , c {\displaystyle a,b,c} 라고 하자. D {\displaystyle D} 위에 적절한 등거리 변환을 가하여 z 3 , z 2 , z 1 {\displaystyle z_{3},z_{2},z_{1}} 을 각각 원점 0, 양의 실수 r ∈ R + {\displaystyle r\in \mathbb {R} ^{+}} , 허수부 Im z > 0 {\displaystyle \operatorname {Im} z>0} 가 0보다 큰 복소수 z {\displaystyle z} 로 옮길 수 있다. 등거리 변환의 성질에 따라 새로운 삼각형 z , r , 0 {\displaystyle z,r,0} 의 세 변 및 세 각은 원래의 삼각형 z 1 , z 2 , z 3 {\displaystyle z_{1},z_{2},z_{3}} 와 같으므로, 새로운 삼각형 z , r , 0 {\displaystyle z,r,0} 에 대하여 증명하는 것으로 족하다. 쌍곡 거리의 정의에 따라, 세 변은 다음과 같다.
a = ln 1 + r 1 − r {\displaystyle a=\ln {\frac {1+r}{1-r}}} b = ln 1 + | z | 1 − | z | {\displaystyle b=\ln {\frac {1+|z|}{1-|z|}}} c = ln | 1 − r z | + | z − r | | 1 − r z | − | z − r | {\displaystyle c=\ln {\frac {|1-rz|+|z-r|}{|1-rz|-|z-r|}}}
여기서 ln {\displaystyle \ln } 은 자연 로그이며, | − | {\displaystyle |-|} 은 복소수의 절댓값이다. 이 셋을 다음과 같이 변형할 수 있다.
tanh a 2 = r {\displaystyle \tanh {\frac {a}{2}}=r} tanh b 2 = | z | {\displaystyle \tanh {\frac {b}{2}}=|z|} tanh c 2 = | z − r | | 1 − r z | {\displaystyle \tanh {\frac {c}{2}}={\frac {|z-r|}{|1-rz|}}}
여기서 tanh {\displaystyle \tanh } 는 쌍곡 탄젠트이다. 쌍곡선 함수의 항등식을 사용한 뒤 위의 결과를 대입하여 정리하면 다음을 얻는다.
cosh c = 2 sinh 2 c 2 + 1 = 2 tanh 2 c 2 1 − tanh 2 c 2 + 1 = 2 | z − r | 2 | 1 − r z | 2 − | z − r | 2 + 1 = 2 r 2 + | z | 2 − 2 r z cos C ( 1 − r 2 ) ( 1 − | z | 2 ) + 1 = ( 1 + r 2 ) ( 1 + | z | 2 ) − 4 r z cos C ( 1 − r 2 ) ( 1 − | z | 2 ) {\displaystyle {\begin{aligned}\cosh c&=2\sinh ^{2}{\frac {c}{2}}+1\\&=2{\frac {\tanh ^{2}{\frac {c}{2}}}{1-\tanh ^{2}{\frac {c}{2}}}}+1\\&=2{\frac {|z-r|^{2}}{|1-rz|^{2}-|z-r|^{2}}}+1\\&=2{\frac {r^{2}+|z|^{2}-2rz\cos C}{(1-r^{2})(1-|z|^{2})}}+1\\&={\frac {(1+r^{2})(1+|z|^{2})-4rz\cos C}{(1-r^{2})(1-|z|^{2})}}\end{aligned}}}
넷째 등호에서 분자 부분은 평면 삼각형 z , r , 0 {\displaystyle z,r,0} 에 대한 평면 코사인 법칙에 따르며, 분모 부분은 절댓값이 실수부와 허수부의 제곱합임에 따라 계산할 수 있다. 이제, 여기에 다음을 대입하면 제1 쌍곡 코사인 법칙의 증명이 완성된다.[6]
cosh a = 1 + tanh 2 a 2 1 − tanh 2 a 2 = 1 + r 2 1 − r 2 {\displaystyle \cosh a={\frac {1+\tanh ^{2}{\frac {a}{2}}}{1-\tanh ^{2}{\frac {a}{2}}}}={\frac {1+r^{2}}{1-r^{2}}}} sinh a = 2 tanh a 2 1 − tanh 2 a 2 = 2 r 1 − r 2 {\displaystyle \sinh a={\frac {2\tanh {\frac {a}{2}}}{1-\tanh ^{2}{\frac {a}{2}}}}={\frac {2r}{1-r^{2}}}} cosh b = 1 + | z | 1 − | z | {\displaystyle \cosh b={\frac {1+|z|}{1-|z|}}} sinh b = 2 | z | 1 − | z | 2 {\displaystyle \sinh b={\frac {2|z|}{1-|z|^{2}}}}
제2 쌍곡 코사인 법칙의 증명 [ 편집 ]
쌍곡 사인 법칙에 나오는 비율의 구체적인 값은 다음과 같다.
sin A sinh a = sin B sinh b = sin C sinh c = 1 − cosh 2 a − cosh 2 b − cosh 2 c + 2 cosh a cosh b cosh c sinh a sinh b sinh c {\displaystyle {\frac {\sin A}{\sinh a}}={\frac {\sin B}{\sinh b}}={\frac {\sin C}{\sinh c}}={\frac {\sqrt {1-\cosh ^{2}a-\cosh ^{2}b-\cosh ^{2}c+2\cosh a\cosh b\cosh c}}{\sinh a\sinh b\sinh c}}}
이에 따라 각 A , B , C {\displaystyle A,B,C} 의 사인 값은 다음과 같다.
sin A = 1 − cosh 2 a − cosh 2 b − cosh 2 c + 2 cosh a cosh b cosh c sinh b sinh c {\displaystyle \sin A={\frac {\sqrt {1-\cosh ^{2}a-\cosh ^{2}b-\cosh ^{2}c+2\cosh a\cosh b\cosh c}}{\sinh b\sinh c}}} sin B = 1 − cosh 2 a − cosh 2 b − cosh 2 c + 2 cosh a cosh b cosh c sinh a sinh c {\displaystyle \sin B={\frac {\sqrt {1-\cosh ^{2}a-\cosh ^{2}b-\cosh ^{2}c+2\cosh a\cosh b\cosh c}}{\sinh a\sinh c}}} sin C = 1 − cosh 2 a − cosh 2 b − cosh 2 c + 2 cosh a cosh b cosh c sinh a sinh b {\displaystyle \sin C={\frac {\sqrt {1-\cosh ^{2}a-\cosh ^{2}b-\cosh ^{2}c+2\cosh a\cosh b\cosh c}}{\sinh a\sinh b}}}
또한, 제1 쌍곡 코사인 법칙에 따라 A , B , C {\displaystyle A,B,C} 의 코사인 값은 다음과 같다.
cos A = cosh b cosh c − cosh a sinh b sinh c {\displaystyle \cos A={\frac {\cosh b\cosh c-\cosh a}{\sinh b\sinh c}}} cos B = cosh a cosh c − cosh b sinh a sinh c {\displaystyle \cos B={\frac {\cosh a\cosh c-\cosh b}{\sinh a\sinh c}}} cos C = cosh a cosh b − cosh c sinh a sinh b {\displaystyle \cos C={\frac {\cosh a\cosh b-\cosh c}{\sinh a\sinh b}}}
따라서, 다음이 성립한다.
cos A cos B + cos C sin A sin B = ( cosh b − cosh c − cosh a ) ( cosh a cosh c − cosh b ) + sinh 2 c ( cosh a cosh b − cosh c ) 1 − cosh 2 a − cosh 2 b − cosh 2 c + 2 cosh a cosh b cosh c = cosh a cosh b cosh 2 c − cosh 2 a cosh c − cosh 2 b cosh c + cosh a cosh b + cosh a cosh b sinh 2 c − cosh c sinh 2 c 1 − cosh 2 a − cosh 2 b − cosh 2 c + 2 cosh a cosh b cosh c = cosh c {\displaystyle {\begin{aligned}{\frac {\cos A\cos B+\cos C}{\sin A\sin B}}&={\frac {(\cosh b-\cosh c-\cosh a)(\cosh a\cosh c-\cosh b)+\sinh ^{2}c(\cosh a\cosh b-\cosh c)}{1-\cosh ^{2}a-\cosh ^{2}b-\cosh ^{2}c+2\cosh a\cosh b\cosh c}}\\&={\frac {\cosh a\cosh b\cosh ^{2}c-\cosh ^{2}a\cosh c-\cosh ^{2}b\cosh c+\cosh a\cosh b+\cosh a\cosh b\sinh ^{2}c-\cosh c\sinh ^{2}c}{1-\cosh ^{2}a-\cosh ^{2}b-\cosh ^{2}c+2\cosh a\cosh b\cosh c}}\\&=\cosh c\end{aligned}}}
마지막 등호에는 항등식 cosh 2 c − sinh 2 c = 1 {\displaystyle \cosh ^{2}c-\sinh ^{2}c=1} 이 사용되었다. 이로써 제2 쌍곡 코사인 법칙이 증명된다.[6]
평면 코사인 법칙과의 관계 [ 편집 ]
평면 코사인 법칙은 제1 구면 및 쌍곡 코사인 법칙의 극한이다. 예를 들어, 평면 코사인 법칙이 제1 쌍곡 코사인 법칙의 극한임을 다음과 같이 보일 수 있다. 푸앵카레 원판의 반지름이 r {\displaystyle r} 일 경우, 제1 쌍곡 코사인 법칙은 다음과 같이 된다.
cosh c r r = cosh a r r cosh b r r − sinh a r r sinh b r r cos C r {\displaystyle \cosh {\frac {c_{r}}{r}}=\cosh {\frac {a_{r}}{r}}\cosh {\frac {b_{r}}{r}}-\sinh {\frac {a_{r}}{r}}\sinh {\frac {b_{r}}{r}}\cos C_{r}}
이 경우, r → ∞ {\displaystyle r\to \infty } 일 때 쌍곡 거리 a r , b r , c r {\displaystyle a_{r},b_{r},c_{r}} 는 유클리드 거리의 2배 2 a ∞ , 2 b ∞ , 2 c ∞ {\displaystyle 2a_{\infty },2b_{\infty },2c_{\infty }} 로 수렴하며, 쌍곡각 A r , B r , C r {\displaystyle A_{r},B_{r},C_{r}} 은 유클리드 각 A ∞ , B ∞ , C ∞ {\displaystyle A_{\infty },B_{\infty },C_{\infty }} 로 수렴한다. 테일러 정리에 따라 다음이 성립한다.
cosh a r r = 1 + 1 2 ( a r r ) 2 + o ( 1 r 2 ) ( r → ∞ ) {\displaystyle \cosh {\frac {a_{r}}{r}}=1+{\frac {1}{2}}\left({\frac {a_{r}}{r}}\right)^{2}+o\left({\frac {1}{r^{2}}}\right)\qquad (r\to \infty )} cosh b r r = 1 + 1 2 ( b r r ) 2 + o ( 1 r 2 ) ( r → ∞ ) {\displaystyle \cosh {\frac {b_{r}}{r}}=1+{\frac {1}{2}}\left({\frac {b_{r}}{r}}\right)^{2}+o\left({\frac {1}{r^{2}}}\right)\qquad (r\to \infty )} cosh c r r = 1 + 1 2 ( c r r ) 2 + o ( 1 r 2 ) ( r → ∞ ) {\displaystyle \cosh {\frac {c_{r}}{r}}=1+{\frac {1}{2}}\left({\frac {c_{r}}{r}}\right)^{2}+o\left({\frac {1}{r^{2}}}\right)\qquad (r\to \infty )}
이를 법칙에 대입하면 다음을 얻는다.
c r 2 r 2 = a r 2 r 2 + b r 2 r 2 − 2 sinh a r r sinh b r r cos C r + o ( 1 r 2 ) ( r → ∞ ) {\displaystyle {\frac {c_{r}^{2}}{r^{2}}}={\frac {a_{r}^{2}}{r^{2}}}+{\frac {b_{r}^{2}}{r^{2}}}-2\sinh {\frac {a_{r}}{r}}\sinh {\frac {b_{r}}{r}}\cos C_{r}+o\left({\frac {1}{r^{2}}}\right)\qquad (r\to \infty )}
다음에 주의하여, 양변에 r 2 {\displaystyle r^{2}} 을 곱한 뒤 극한 r → ∞ {\displaystyle r\to \infty } 을 취하고 다시 양변에 4를 나누자.
lim r → ∞ r sinh a r r = 2 a ∞ {\displaystyle \lim _{r\to \infty }r\sinh {\frac {a_{r}}{r}}=2a_{\infty }} lim r → ∞ r sinh b r r = 2 b ∞ {\displaystyle \lim _{r\to \infty }r\sinh {\frac {b_{r}}{r}}=2b_{\infty }} lim r → ∞ r sinh b r r = 2 c ∞ {\displaystyle \lim _{r\to \infty }r\sinh {\frac {b_{r}}{r}}=2c_{\infty }}
그러면 평면 코사인 법칙을 얻는다.[6]
c ∞ 2 = a ∞ 2 + b ∞ 2 − 2 a ∞ b ∞ cos C ∞ {\displaystyle c_{\infty }^{2}=a_{\infty }^{2}+b_{\infty }^{2}-2a_{\infty }b_{\infty }\cos C_{\infty }}
제2 쌍곡 코사인 법칙
cos C r = − cos A r cos B r + sin A r sin B r cosh c r r {\displaystyle \cos C_{r}=-\cos A_{r}\cos B_{r}+\sin A_{r}\sin B_{r}\cosh {\frac {c_{r}}{r}}}
에 극한 r → ∞ {\displaystyle r\to \infty } 을 취하면 다음과 같은 자명한 항등식이 된다.
cos C ∞ = − cos A ∞ cos B ∞ + sin A ∞ sin B ∞ {\displaystyle \cos C_{\infty }=-\cos A_{\infty }\cos B_{\infty }+\sin A_{\infty }\sin B_{\infty }}
이는 A ∞ + B ∞ + C ∞ = π {\displaystyle A_{\infty }+B_{\infty }+C_{\infty }=\pi } 이므로 자명하다. 따라서 유클리드 기하학에는 제2 코사인 법칙이 존재하지 않는다.[6]
같이 보기 [ 편집 ]
각주 [ 편집 ]
코사인법칙, 제2 코사인법칙 증명
코사인법칙 두 번째 제2 코사인법칙이에요.
제2 코사인법칙은 제1 코사인법칙의 확장판이에요. 따라서 제1 코사인법칙에 대해서 알고 있어야 하고 증명도 할 줄 알아야 해요.
이 글에서는 제2 코사인법칙을 유도해보고 제2 코사인법칙을 활용해서 문제도 풀어볼 거예요. 제2 코사인법칙이 무엇을 의미하는지 어떤 경우에 제2 코사인법칙을 이용해서 문제를 푸는지 잘 기억해두세요.
제2 코사인법칙 증명
제2 코사인법칙을 보기 전에 먼저 제1 코사인법칙부터 볼까요?
a = bcosC + ccosB
b = ccosA + acosC
c = acosB + bcosA
세 개의 식이 있는데 각각의 식에 좌변에 있는 항목(a, b, c)을 양변에 곱해보죠.
a 2 = abcosC + cacosB …… ①
= abcosC + cacosB …… ① b 2 = bccosA + abcosC …… ②
= bccosA + abcosC …… ② c2 = cacosB + bccosA …… ③
순서대로 ①식, ②식, ③식이라고 해보죠.
① – ② – ③을 하면
a2 – b2 – c2 = abcosC + cacosB – (bccosA + abcosC) – (cacosB + bccosA)
a2 – b2 – c2 = -2bccosA
a2 = b2 + c2 – 2bccosA
② – ③ – ①을 하면
b2 – c2 – a2 = bccosA + abcosC – (cacosB + bccosA) – (abcosC + cacosB)
b2 – c2 – a2 = -2cacosB
b2 = c2 + a2 – 2cacosB
③ – ① – ②를 하면
c2 – a2 – b2 = cacosB + bccosA – (abcosC + cacosB) – (bccosA + abcosC)
c2 – a2 – b2 = -2abcosC
c2 = a2 + b2 – 2abcosC
제2 코사인법칙
a2 = b2 + c2 – 2bccosA
b2 = c2 + a2 – 2cacosB
c2 = a2 + b2 – 2abcosC
일단 첫 번째 공식만 보죠. a2 = b2 + c2 – 2bccosA
각 항을 보면 a, b, c라는 세 변의 길이와 A라는 한 각의 크기로 되어 있어요. 세 변과 한 각 사이의 관계를 나타내는 식이죠.
b, c라는 두 변의 길이와 A의 각의 크기를 알면 나머지 한 변인 a를 구할 수 있어요. 여기서 A는 어떤 각인가요? a의 대변이자 b, c 사이의 끼인각이죠? 즉 두 변의 길이와 그 끼인각의 크기를 알면 끼인각의 대변의 길이를 구할 수 있다는 거예요.
조금 돌려서 얘기해볼까요?
a, b, c 세 변의 길이를 알면 어떨까요? cosA를 구할 수 있죠? 만약에 cosA가 우리가 외우고 있는 삼각비라면 A도 구할 수 있다는 얘기예요.
다음을 구하여라.
(1) a = 2cm, b = 3cm, C = 60°일 때, c
(2) a = 3cm, b = 3cm, c = 3 cm일 때, A
(1) 두 변의 길이와 그 끼인각의 크기를 알려줬네요. 공식에 대입해보죠.
(2) 세 변의 길이를 알려주고 한 각의 크기를 구하라고 했어요. 코사인법칙은 세 변의 길이와 한 각의 관계를 나타내는 식이니까 공식을 이용해서 각을 구할 수 있어요.
A = 45°
함께 보면 좋은 글
사인법칙, 사인법칙 증명
코사인법칙, 제1코사인법칙 증명
삼각방정식, 삼각방정식 푸는 방법
삼각부등식, 삼각부등식 푸는 법
삼각함수 그래프 그리는 법 – sin 그래프, 주기함수
정리해볼까요 제2 코사인법칙 a 2 = b 2 + c 2 – 2bccosA
= b + c – 2bccosA b 2 = c 2 + a 2 – 2cacosB
= c + a – 2cacosB c2 = a2 + b2 – 2abcosC
그리드형(광고전용)
제1,2코사인법칙
사인법칙에 이어 코사인법칙에 대해 설명하겠습니다.
저에겐 옛날 수학(하) 책과 미적분2 정석책이 있어서 두 책의 삼각함수를 찾아보다 알게 되었는데
미적분2가 아무래도 개정과정이다보니까 내용의 상당수가 빠져있더군요.
그렇게 중요하진 않지만 미적분2에는 제1코사인법칙이 언급되어 있지 않고
제2코사인법칙만 코사인법칙이라 하며 소개되어 있습니다.
그래도 저는 제1코사인법칙도 알아두는 것이 좋다고 생각하는 이유가 제1코사인법칙을 이용하여 제2코사인법칙을 증명해낼 수 있기때문이죠.
우선 제1코사인법칙부터 소개하겠습니다.
제1코사인법칙이란 삼각형 ABC에서 아래와 같은 관계를 만족한다는것입니다.
증명과정이 간단한데, 사실 이건 당연하다고 할 수 있습니다. 삼각형 A에서 그은 수선을 발을 H라고하면 선분 BH는 c*cosB, 선분 CH는 b*cosC로 나타낼 수 있어 a=b*cosC+b*cosC로 나타낼수 있는 것이죠. 같은 방법으로 수선의 발을 내려 길이를 코사인의 합으로 나타내면 되겠습니다.
다음으로 제2코사인법칙을 알아보겠습니다.
제2코사인법칙이란 삼각형 ABC에서
이것의 증명방법은 두 가지가 있습니다.
첫번째로 제1코사인법칙을 이용한 증명방법입니다.
다음으로 도형을 이용한 증명방법입니다.
1.각 A가 예각일때,
삼각형 ABC에서 C에서 내린 수선의 발을 H라고 할때 H의 위치에 따라 왼쪽의 경우는 선분BH=c-bcosx, 오른쪽의 경우는 선분BH=bcosx-c이므로 직각삼각형 BHC에서
2.각 A가 직각일때,
이 경우는 를 만족합니다. 이게 곧 피타고라스 정리이죠.
3. 각 A가 둔각일때,
이 경우는 이므로 직각삼각형 BHC에서 예각일때와 같은 이유로 제2코사인법칙이 성립합니다.
지금까지 코사인법칙에 대해 알아봤는데요
개정교육과정에서 제1코사인법칙이 빠졌지만 제2코사인법칙과 같이 알아두면 좋을것 같습니다.
코사인법칙의 중요성은 각을 길이를 이용해 나타낼 수 있고, 삼각형에서 한 변의 길이를 다른 두 변의 길이와 끼인각을 이용하여 나타낼 수 있다는 것입니다.
참고로 제2코사인법칙은 기하문제를 풀때 유용하게 쓰이니 꼭 알아두셨으면 합니다.
So you have finished reading the 제 2 코사인 법칙 topic article, if you find this article useful, please share it. Thank you very much. See more: 제1코사인법칙, 제 3 코사인법칙, 제2코사인법칙 영어로, 제 2 코사인 법칙 계산기, 제2코사인법칙 벡터 증명, 제1코사인법칙 교육과정, 사인법칙 코사인법칙, 코사인법칙 활용

