Top 49 맨 휘트니 검정 Best 268 Answer

You are looking for information, articles, knowledge about the topic nail salons open on sunday near me 맨 휘트니 검정 on Google, you do not find the information you need! Here are the best content compiled and compiled by the https://chewathai27.com/to team, along with other related topics such as: 맨 휘트니 검정 mann-whitney u test, 비모수검정 종류, 맨-휘트니 검정 엑셀, mann-whitney u test z값, Mann Whitney U test Wilcoxon rank sum, Mann-Whitney t test, mann-whitney u test python, Mann-Whitney U test calculator

SPSS를 활용한 비모수통계 – (10) 맨-휘트니 검정/윌콕슨 순위합 검정 (Mann-Whitney Test)/(Wilcoxon Rank-Sum Test)

비모수 검정: Mann-Whitney U Test 외

Article author: mj91.tistory.com
Reviews from users: 17536 Ratings
Top rated: 3.7
Lowest rated: 1
Summary of article content: Articles about 비모수 검정: Mann-Whitney U Test 외 (= 만-위트니-윌콕슨 검정 Mann-Whitney-Wilcoxon test = 윌콕슨 순위 합 검정 Wilcoxon rank sum test). “두 집단의 짝지어진 관측치가 같은 분포?” …
Most searched keywords: Whether you are looking for 비모수 검정: Mann-Whitney U Test 외 (= 만-위트니-윌콕슨 검정 Mann-Whitney-Wilcoxon test = 윌콕슨 순위 합 검정 Wilcoxon rank sum test). “두 집단의 짝지어진 관측치가 같은 분포?” 1. Nonparametric Statistics 비모수 통계학 통계학은 모수 통계학과 비모수 통계학으로 나눌 수 있습니다. 모수 통계학은 모집단이 정규분포라는 가정이 필요하지만, 비모수 통계학은 분포에 대한 가정 없이 가설..
Table of Contents:

1 Nonparametric Statistics 비모수 통계학

2 Normality Check 정규성 확인

3 Rank Correlation 순위 상관 계수

4 비모수 검정 (1) Mann-Whitney U Test

4 비모수 검정 (2) Wilcoxon (Matched Pairs) Signed-Rank Test

4 비모수 검정 (3) Kruskal-Wallis H test

4 비모수 검정 (4) Friedman test

‘ITSWDataCloud코딩’ Related Articles

검색

최근 포스트

전체 방문자

티스토리툴바

Article author: www.ibm.com
Reviews from users: 44343 Ratings
Top rated: 4.4
Lowest rated: 1
Summary of article content: Articles about Mann-Whitneyì U ê²ì Mann-Whitney는 2표본 모집단의 위치가 같은지 검정합니다. 두 그룹의 관측값은 서로 조합되어 동률시 할당되는 평균 순위로 순위가 지정됩니다. 동률의 수는 전체 관측값 … …
Most searched keywords: Whether you are looking for Mann-Whitneyì U ê²ì Mann-Whitney는 2표본 모집단의 위치가 같은지 검정합니다. 두 그룹의 관측값은 서로 조합되어 동률시 할당되는 평균 순위로 순위가 지정됩니다. 동률의 수는 전체 관측값 … ë¹ëª¨ì ê²ì , Mann-Whitneyì U ê²ì
Table of Contents:

ë°ì´í° ê³ ë ¤ì¬í

Mann-Whitneyì U ê²ì êµ¬íê¸°

Mann-Whitneyì U ê²ì

Article author: thduddl2486.tistory.com
Reviews from users: 34114 Ratings
Top rated: 4.4
Lowest rated: 1
Summary of article content: Articles about [SPSS 분석] Mann-Whitney 검정 [SPSS 분석] Mann-Whitney 검정 · 1) 정의. 독립표본 t-검정(Independent sample t-test)은 두 집단 간 평균치의 차이를 비교하는 통계 검정 방법입니다. …
Most searched keywords: Whether you are looking for [SPSS 분석] Mann-Whitney 검정 [SPSS 분석] Mann-Whitney 검정 · 1) 정의. 독립표본 t-검정(Independent sample t-test)은 두 집단 간 평균치의 차이를 비교하는 통계 검정 방법입니다. 1. Mann-Whitney 검정 1) 정의 독립표본 t-검정(Independent sample t-test)은 두 집단 간 평균치의 차이를 비교하는 통계 검정 방법입니다. 독립표본이란, 모집단에서 표본을 추출할 때 비교하려는 두 표본 간..
Table of Contents:

태그

최근글

비모수 검정: Mann-Whitney U Test 외

반응형

1. Nonparametric Statistics 비모수 통계학

통계학은 모수 통계학과 비모수 통계학으로 나눌 수 있습니다.

모수 통계학은 모집단이 정규분포라는 가정이 필요하지만,

비모수 통계학은 분포에 대한 가정 없이 가설검정을 수행할 수 있습니다.

모수 데이터: 알려진 확률분포를 지닌 모집단에서 나온 데이터

비모수 데이터: 확인되지 않은 확률분포를 지닌 모집단에서 나온 데이터

모수 통계학에서는 평균(Mean)이 중요한 반면,

비모수 통계학에서는 중위수(Median)이 중요합니다.

검정하는 내용도 둘 이상의 데이터셋이 같은 평균을 가지는지 확인하는 모수 통계학과는 달리,

비모수 통계학에서는 둘 이상의 데이터셋의 중심위치가 같은 지를 검정합니다.

데이터가 먼저 가우시안 분포 (정규분포)를 따르는지 확인하고

따르지 않으면 비모수 통계학의 방법을 사용하면 되는데,

정규성 확인에 사용할 수 있는 테스트의 종류들에는 대표적으로 다섯 개가 있습니다.

그래프를 이용한 방법으로는 히스토그램, Q-Q plot 이 있고

통계적 검정을 이용하는 방법으로는 Shapiro-Wilk test, D’Agostino’s K^2 test, Anderson-Darling test가 있습니다.

샤피로 윌크 검정을 귀무가설은 정규분포를 따른다는 것이고

유의확률이 0.05보다 낮으면 귀무가설을 기각하면 됩니다.

모수검정 설명 모수검정 각 모수검정에 대응하는 비모수검정 “두 집단의 관측치가 같은 분포? median 동일?”

두 개 그룹간의 평균에 차이가 나는지를 보는 검정.

샘플 각각의 평균값을 찾아서 그 두 개의 평균 값을 비교하는 것. two sample t-test 만-위트니 U 검정 Mann-Whitney U test

(= 만-위트니-윌콕슨 검정 Mann-Whitney-Wilcoxon test

= 윌콕슨 순위 합 검정 Wilcoxon rank sum test) “두 집단의 짝지어진 관측치가 같은 분포?”

데이터셋 2개의 차이 값들의 평균을 검정.

차이 (difference) 데이터셋을 one sample t-test 하는 것과 동일함. paired sample t-test 윌콕슨 부호 순위 검정

Wilcoxon signed-rank test “셋 이상 집단의 관측치가 같은 분포?”

분산을 이용해서 평균을 추론.

세 집단 이상 비교.

출력 변수에 대한 1개의 입력 변수 의 3개 이상의 그룹 의 평균들 one way ANOVA 크루스칼-왈리스 검정

Kruskal-Wallis H test

(=순위 기반 일원분산분석

one-way ANOVA on ranks) “셋 이상 집단의 관측치가 같은 분포?”

출력 변수에 대한 2 개의 입력 변수 의 3개 이상의 그룹들 의 상호 간의 영향 검정 two way ANOVA 프리드먼 테스트

Friedman test

윌콕슨 부호 순위 검정 Wilcoxon signed-rank test

– 부호와 상대적 크기를 고려해 중앙값을 검정함.

– 분포의 연속성, 독립성, 대칭성을 가정함.

런 검정 Run Test

– 각 표본이 서로 독립적인지 검정. 패턴/경향 없이 랜덤한지 검정.

* Run : 표본의 부호가 바뀔 때까지의 묶음. 런의 수가 상한치/하한치 범위를 벗어나면 H0를 기각.

크루스칼-왈리스 H 검정

– k 개의 표본이 서로 다른 모집단에서 나왔는가를 검정

– 모집단에 대한 정규성, 등분산성의 가정 성립 여부에 대한 확신이 없음

– 측정치: 표본 내외 모두 독립, 연속적

– 귀무가설: k개의 모집단의 중위수가 모두 같다.

프리드먼 테스트

– 측정값들이 동일한 모집단에서 나왔는가 검정

– 그룹 간 차이를 검정하는 것이 아니라, 레코드 간 차이가 없다는 귀무가설에 대해 검정

– 그룹과 레코드의 교호작용 (interaction effect)은 없다는 전제가 있음

– 자료를 순위로 표현한 후, 교차표를 작성하고 순위합을 구한다.

집단 1개 Run test, Kolmogorov-Smirnov 검정, 부호검정 집단 2개 Kolmogorov-Smirnov 검정, 윌콕슨 순위 합 검정(=만-위트니 U 검정), 윌콕슨 부호 순위 검정 집단 3개 크루스칼-왈리스 검정 (입력변수 1개), 프리드먼 테스트 (입력변수2개)

2. Normality Check 정규성 확인

먼저, 데이터가 정규분포를 따르는지 확인해야 합니다.

확인하는 방법에는 여러가지가 있는데,

선형적으로 나타내기 때문에 객관적으로 볼 수 있는 방법으로 Quantile-Quantile plot 이 있습니다.

확인해본 결과 정규 분포를 따르지 않는다고 나왔는데

모수 통계학을 사용하고 싶다면 정규분포를 따르도록 데이터를 바꿔줄 수도 있습니다.

정규 분포를 따르지 않는 데이터를 정규 분포를 따르도록 변환하는 방법에는

1) 샘플 크기를 증가 시키거나,

2) 데이터에 소수가 있으면 소수점 아래 자릿수를 늘리거나,

3) 아웃라이어를 제거하거나,

4) 롱테일을 제거하거나,

5) 멱변환(Power transform)

6) 로그 변환(log transformation)(로그 취하기)

7) 박스-칵스 Box-Cox 변환

등이 있습니다.

정규 분포를 따르지 않는 데이터를 비모수 통계학을 사용하여 가설검정을 수행할 때는

순위 (rank) 를 주로 활용할 수 있습니다.

3. Rank Correlation 순위 상관 계수

상관계수 데이터의 정규성 관계 Pearson

피어슨 상관계수 정규분포를 따르는 데이터 연속형의 두 변수 선형적 Spearman

스피어만 상관계수 정규분포를 벗어나는 데이터 연속형, 이산형 순위 rank 사용 비선형적. 단조적 Kendall’s Tau

켄달의 타우 상관계수 정규분포를 벗어나는 데이터 순위 rank 사용

피어슨 상관계수는 두 변수의 공분산을 표준편차의 곱으로 나눈 값으로 비선형 관계는 측정하지 못합니다.

스피어만 상관계수는 이산형 변수 간의 상관계수도 구할 수 있습니다.

4. 비모수 검정 (1) Mann-Whitney U Test

아래에 예시로 사용한 데이터셋 A의 평균은 6이고 데이터셋 B의 평균은 6.25 입니다. 이 정도의 차이를 Mann-Whitney U Test 에서는 두 그룹의 평균에 차이가 없다고 할지 있다고 할지 검정해보겠습니다.

Mann-Whitney U Test의 귀무가설 H0는 두 그룹이 차이가 없다는 것이고

대립가설 H1 는 두 그룹에 차이가 있다는 것입니다.

먼저, Mann-Whitney 에서 사용하는 U값을 구합니다.

U값을 구하려면 각 데이터셋을 정렬하고 순위를 구한 뒤,

아래 테이블의 우측 2개 열에 설명해둔 작업을 수행하여 각 셋 별 순위의 합을 구합니다.

data A 정렬 data B 정렬 data A 순위 data B 순위 3 (1위) 1위 5 (2위) 5 (2위) 2위,3위,4위의 평균ㅡ> 3위 2위,3위,4위의 평균 ㅡ> 3위 5 (2위) 2위,3위,4위의 평균 ㅡ> 3위 6 (5위) 5위 7 (6위) 7 (6위) 6위,7위의 평균 ㅡ> 6.5위 6위,7위의 평균 ㅡ> 6.5위 8 (8위) 8위 9 (9위) 9위 데이터셋 A의 원소의 개수는 5개 (na 라고 하겠음) 데이터셋B의 원소의 개수는 4개 (nb 라고 하겠음) 순위의 합 = 1 + 3 + 5 + 6.5 + 9 = 24.5 (Ra라 하겠음) 순위의 합 = 3 + 3 + 6.5 + 8 = 20.5 (Rb라 하겠음)

데이터셋 A의 U 값 = na*nb + (na*(na+1))/2 – Ra = 5*4 +5*6/2 – 24.5 = 10.5

데이터셋 B의 U 값 = na*nb + (nb*(nb+1))/2 – Rb = 5*4 +4*5/2 – 20.5 = 9.5

두 U 값 중 더 작은 값이 최종 U 값이 됩니다. 즉, 여기서는 9.5 입니다.

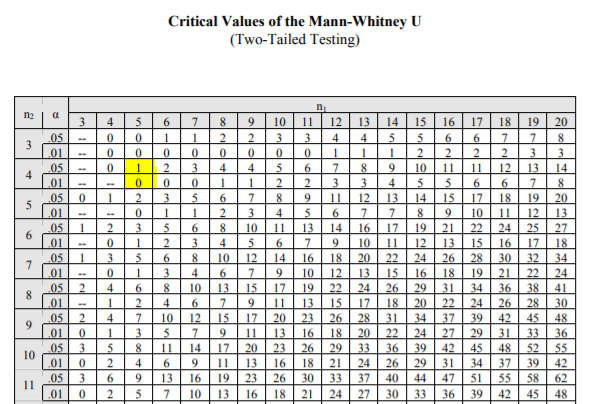
그러면 이제 이 값을 Critical Values of the Mann-Whitney U 테이블에서 찾아봅니다.

n1이 na이고 n2가 nb로 보면 됩니다. 만나는 지점을 찾으면 됩니다.

아래 그림 테이블 왼편의 a 는 유의수준을 뜻합니다.

즉 위 예시에서는 5개와 4개였으므로,

n1= 5 이고 n2 = 4 인 지점을 찾으면

유의수준 0.05일때는 1 이고 유의수준 0.01 일 때는 0이란 값이

귀무가설을 기각할 수 있는 임계치라는 뜻입니다.

유의수준 0.05일때 1보다 작으면 귀무가설을 기각할 수 있는데 여기서는 9.5 였으므로

귀무 가설을 기각할 수 없습니다.

즉, 두 그룹은 평균에 차이가 없다고 보았습니다.

출처 : https://ocw.umb.edu/psychology/psych-270/other-materials/RelativeResourceManager.pdf

4. 비모수 검정 (2) Wilcoxon (Matched Pairs) Signed-Rank Test

Wilcoxon signed-rank test 는 Mann-Whitney U test 와 유사합니다.

다만, paired t-test 와 같이, 두 개 데이터셋의 차이를 구하는 것이고,

여기서는 차이의 크기를 부호가 있는 순위로 매겨서 사용합니다.

그 후 양의 부호인 순위들의 합을 구하고, 음의 부호인 순위들의 합을 구한 후,

둘 중에 작은 값을 최종 검정 통계량 값으로 취합니다.

검정 통계량 값을 구했으면 Mann-Whitney U test 에서와 같이 기각역 값들이 적힌 테이블을 확인합니다.

만약, 유의수준이 0.05이면, a = 0.025 인 기각역과, a = 0.975 인 기각역을 찾아서,

위에서 구했던 최종 검정 통계량 값과 비교합니다.

기각역에 속한다면 귀무가설을 기각합니다.

Wilcoxon signed-rank test 에서도 H0는 ‘차이가 없다’이고, 대립가설 H1은 ‘차이가 있다’입니다.

즉, 귀무가설을 기각하면 두 개 데이터셋의 차이가 있다는 결론을 내리게 됩니다.

4. 비모수 검정 (3) Kruskal-Wallis H test

Kruskal-Wallis H test는 2개 표본에 사용하는 Mann-Whitney U Test 를 다변량 분석으로 확장시킨 것입니다.

여기서의 귀무가설은 ‘k개의 모집단의 중위수가 모두 같다’는 것이고

대립가설은 ‘k개의 모집단의 중위수가 모두 같지는 않다’입니다.

Kruskal-Wallis H test는 각 표본을 정렬하여 순위를 매긴 후, 순위를 합하여

각각의 데이터셋들에 대한 순위합을 구합니다.

그리고 Kruskal-Wallis H test의 검정 통계량인 H 값을 구하는 계산 공식을 통해 H 값을 구합니다.

(그런데 이 공식에서 분자에 12라는 상수는 왜 12를 쓰는 것일까요?)

그 후 그 H 값이 기각역에 포함된다면 귀무가설을 기각합니다.

4. 비모수 검정 (4) Friedman test

Friedman test도 다변량 분석입니다.

이 검정은 교호작용이 없다는 가정을 전제로 하는데,

이 부분은 Friedman test의 한계점이기도 합니다.

프리드먼 검정은 세 개 이상 그룹을 비교할 때 사용합니다.

반응형

Mann-Whitney의 U 검정

Mann-Whitney의 U 검정 프로시저는 각 케이스의 순위를 사용하여 그룹이 동일한 모집단에서 비롯되는지 여부를 검정합니다. Mann-Whitney는 2표본 모집단의 위치가 같은지 검정합니다. 두 그룹의 관측값은 서로 조합되어 동률시 할당되는 평균 순위로 순위가 지정됩니다. 동률의 수는 전체 관측값 수보다 작아야 합니다. 모집단의 위치가 똑같을 때는 두 표본 간의 순위가 무작위로 혼합됩니다. 검정을 통해 그룹 1의 스코어가 그룹 2의 스코어보다 앞선 횟수와 그룹 2의 스코어가 그룹 1의 스코어보다 앞선 횟수를 계산합니다.

예 더 편안하고 보기에도 좋으며 빠르게 치아를 교정할 수 있도록 새로운 치열 교정기가 개발되었습니다. 새 치열 교정기를 착용할 수 있는 기간을 이전 교정기와 비교하기 위해 이전 교정기를 착용할 어린이 10명과 새 교정기를 착용할 어린이 10명을 임의로 선택합니다. Mann-Whitney의 U 검정을 통해 새 교정기를 착용한 어린이의 경우 대체로 이전의 교정기를 착용한 어린이보다 짧은 기간에 같은 효과를 얻을 수 있음을 알 수 있습니다. Statistics 평균, 표준편차, 최소, 최대, 비결측 케이스 수 및 사분위수를 선택할 수 있습니다. 검정: Mann-Whitney의 U

데이터 고려사항 데이터 순서를 지정할 수 있는 숫자변수를 사용합니다. 가정 독립 표본과 무작위 표본을 사용합니다. Mann-Whitney U 검정은 두 개 분포가 동일한지 검정합니다. 두 분포 사이의 위치에서 차이를 검정하는 데 사용하려면 두 분포의 형태가 같다고 가정해야 합니다.

[SPSS 분석] Mann-Whitney 검정

반응형

1. Mann-Whitney 검정

1) 정의

독립표본 t-검정(Independent sample t-test)은 두 집단 간 평균치의 차이를 비교하는 통계 검정 방법입니다. 독립표본이란, 모집단에서 표본을 추출할 때 비교하려는 두 표본 간에 서로 영향을 받지 않고, 독립적으로 추출된 표본으로 한 집단의 측정치가 또 다른 집단의 측정치에 영향을 미치지 않는 독립성이 보장된 자료를 의미합니다. 독립변수는 범주형 자료, 종속변수는 연속형 자료인 경우에 활용합니다.

집단 간의 독립성은 가정되지만, 정규분포를 따르지 않을 때 독립표본 t-test를 대신하여 비모수 통계인 Mann-Whitney test를 시행합니다.

2) 가설 설정

성별에 따라 우울 정도에 차이가 있는지 검정하고자 한다면, 성별은 남성과 여성으로 분류되는 범주형 자료이고, 우울 정도는 연속형 자료입니다. 성별에 따른 우울 정도에 차이가 있는지 알아보기 위해 독립표본 t-검정을 실시합니다. 하지만 표본 수가 20개이고, 정규분포를 따르지 않기 때문에 비모수 통계인 Mann-Whitney 검정을 실시합니다.

① 가설 : 독립변수(범주형)에 따라 종속변수(연속형)는 유의한 차이가 있다.

② 귀무가설 : 성별에 따라 우울 정도는 유의한 차이가 없다.

③ 대립가설 : 성별에 따라 우울 정도는 유의한 차이가 있다.

3) Mann-Whitney test

① 메뉴를 선택합니다.

② ‘집단변수’ 입력칸에 독립변수인 성별을 지정하고, ‘검정 변수’ 입력칸에 종속변수인 우울을 지정합니다.

③ 검정 변수를 클릭하면 ‘집단 정의’ 버튼이 활성화 되지 않습니다. 집단 변수 입력칸에 지정한 ‘성별’을 클릭하여, ‘집단 정의’ 버튼을 활성화 시켜 클릭합니다.

④ 집단 1에 숫자 1, 집단 2에 숫자 2를 입력하고, ‘계속’을 클릭합니다.

⑤ ‘옵션’을 클릭하고, ‘통계량’에서 기술통계를 지정하고, ‘계속’을 클릭합니다.

⑥ ‘확인’을 클릭합니다.

⑦ 검정 통계량을 먼저 확인합니다. 근사 유의확률(양측)은 .791로 .05보다 높은 것을 알 수 있습니다. 즉, 성별에 따른 우울 정도는 유의한 차이가 없는 것으로 나타났습니다.

⑧ 만약 유의확률이 .05보다 낮다는 가정 하에 해석을 계속하자면, 남성의 우울 평균 순위는 11.33으로 여성의 우울 평균 순위인 10.35보다 높으므로 남성이 더 우울하다고 할 수 있습니다.

So you have finished reading the 맨 휘트니 검정 topic article, if you find this article useful, please share it. Thank you very much. See more: mann-whitney u test, 비모수검정 종류, 맨-휘트니 검정 엑셀, mann-whitney u test z값, Mann Whitney U test Wilcoxon rank sum, Mann-Whitney t test, mann-whitney u test python, Mann-Whitney U test calculator

Top 49 맨 휘트니 검정 Best 268 Answer

비모수 검정: Mann-Whitney U Test 외

Mann-Whitneyì U ê²ì

[SPSS 분석] Mann-Whitney 검정

6. 통계 검정 기초 : Wilcoxon Rank sum 검정/Mann Whitney U 검정 예제, 정규분포가 아닐때

Mann-Whitney ê²ì ì ëí ëª¨ë íµê³ë í´ì – Minitab

[내가 하는 통계 분석] 윌콕슨 순위합 검정(Wilcoxon rank sum test) or 맨-휘트니 U 검정(Mann-Whitney U test) in R

비모수 검정: Mann-Whitney U Test 외

Mann-Whitney의 U 검정

[SPSS 분석] Mann-Whitney 검정

Leave a Comment Cancel reply

비모수 검정: Mann-Whitney U Test 외

Mann-Whitneyì U ê²ì 

[SPSS 분석] Mann-Whitney 검정

6. 통계 검정 기초 : Wilcoxon Rank sum 검정/Mann Whitney U 검정 예제, 정규분포가 아닐때

Mann-Whitney ê²ì ì ëí ëª¨ë íµê³ë í´ì – Minitab

[내가 하는 통계 분석] 윌콕슨 순위합 검정(Wilcoxon rank sum test) or 맨-휘트니 U 검정(Mann-Whitney U test) in R

비모수 검정: Mann-Whitney U Test 외

Mann-Whitney의 U 검정

[SPSS 분석] Mann-Whitney 검정

Leave a Comment Cancel reply

Mann-Whitneyì U ê²ì

Mann-Whitney ê²ì ì ëí ëª¨ë íµê³ë í´ì – Minitab