Top 17 머신 러닝 회귀 분석 The 43 New Answer

You are looking for information, articles, knowledge about the topic nail salons open on sunday near me 머신 러닝 회귀 분석 on Google, you do not find the information you need! Here are the best content compiled and compiled by the https://chewathai27.com/to team, along with other related topics such as: 머신 러닝 회귀 분석 머신러닝 회귀분석 차이, 머신러닝 회귀분석 예제, 머신러닝 회귀 알고리즘, 머신러닝 다중회귀분석, 회귀분석 데이터셋, 머신러닝 회귀 모델, 머신러닝 회귀 알고리즘 종류, 머신러닝 회귀란

Machine learning 1 – 17. 회귀

머신 러닝 회귀 분석

Article author: blog.mathpresso.com
Reviews from users: 32983 Ratings
Top rated: 4.1
Lowest rated: 1
Summary of article content: Articles about 머신 러닝 회귀 분석 머신러닝 개념도. 가설(방정식이) 몇차 방정식인지? 그리고 계수는 각각 무엇인지 알아보는 것입니다. 이 방정식의 계수가 선형이면 선형 회귀 분석(Linear Regression … …
Most searched keywords: Whether you are looking for 머신 러닝 회귀 분석 머신러닝 개념도. 가설(방정식이) 몇차 방정식인지? 그리고 계수는 각각 무엇인지 알아보는 것입니다. 이 방정식의 계수가 선형이면 선형 회귀 분석(Linear Regression …
Table of Contents:

머신 러닝 회귀 분석

Article author: velog.io
Reviews from users: 31944 Ratings
Top rated: 4.6
Lowest rated: 1
Summary of article content: Articles about 회귀 (Regression)란? 회귀분석의 개념. 머신러닝 회귀 예측의 핵심은 주어진 피처와 결정 값 데이터 기반에서 학습을 통해 최적의 회귀 계수를 찾아내는 것이다. …
Most searched keywords: Whether you are looking for 회귀 (Regression)란? 회귀분석의 개념. 머신러닝 회귀 예측의 핵심은 주어진 피처와 결정 값 데이터 기반에서 학습을 통해 최적의 회귀 계수를 찾아내는 것이다. 회귀 개념
Table of Contents:

Article author: www.appier.com
Reviews from users: 25289 Ratings
Top rated: 3.6
Lowest rated: 1
Summary of article content: Articles about 회귀분석 기법의 5가지 일반 유형과 각각의 활용 방법 1. 선형 회귀(Linear regression). 머신러닝에서 가장 일반적인 회귀분석 유형이라고 할 수 있는 선형 회귀는 예측 변수와 종속 변수로 구성되며, 이 둘은 … …
Most searched keywords: Whether you are looking for 회귀분석 기법의 5가지 일반 유형과 각각의 활용 방법 1. 선형 회귀(Linear regression). 머신러닝에서 가장 일반적인 회귀분석 유형이라고 할 수 있는 선형 회귀는 예측 변수와 종속 변수로 구성되며, 이 둘은 … 회귀분석은 데이터 분석에 사용되는 매우 강력한 머신러닝 도구이다. 어떻게 작동하는지, 주요 유형에는 어떤 것들이 있는지, 그리고 비즈니스에 어떤 도움을 주는지 알아보자. 머신러닝에서 회귀분석의 의미 회귀분석은 종속 변수(목표)와 하나 이상의 독립 변수(예측 변수라고도 함)
Table of Contents:

Article author: roytravel.tistory.com
Reviews from users: 44557 Ratings
Top rated: 4.7
Lowest rated: 1
Summary of article content: Articles about [머신러닝 이론] 회귀 (Regression) :: For a better world. 회귀는 여러 개의 독립변수와 한 개의 종속변수 간의 상관관계를 모델링하는 기법을 통칭한다. 예를 들어 아파트의 방 개수, 방 크기, 주변 학군 등 여러 … …
Most searched keywords: Whether you are looking for [머신러닝 이론] 회귀 (Regression) :: For a better world. 회귀는 여러 개의 독립변수와 한 개의 종속변수 간의 상관관계를 모델링하는 기법을 통칭한다. 예를 들어 아파트의 방 개수, 방 크기, 주변 학군 등 여러 … 회귀 소개 회귀는 현대 통계학을 떠받치고 있는 주요 기둥 중 하나이다. 회귀 기반의 분석은 엔지니어링, 의학, 사회과학, 경제학 등의 분야가 발전하는 데 크게 기여해왔다. 회귀 분석은 유전적 특성을 연구하던..My dream is to live for the growth of humanity. I live for helping people who are in need and don’t have equal education opportunities and who have an illness but can’t afford treatment.
Table of Contents:

[머신러닝 이론] 회귀 (Regression) :: For a better world.

Article author: kimdingko-world.tistory.com
Reviews from users: 28835 Ratings
Top rated: 3.8
Lowest rated: 1
Summary of article content: Articles about [머신러닝 완벽가이드] 회귀(Regression)와 경사하강법(Gradient Descent) 이러한 경험적 연구 이후, 칼 피어슨은 아버지와 아들의 키를 조사한 결과를 바탕으로 함수 관계를 도출하여 회귀분석 이론을 수학적으로 정립하였다. …
Most searched keywords: Whether you are looking for [머신러닝 완벽가이드] 회귀(Regression)와 경사하강법(Gradient Descent) 이러한 경험적 연구 이후, 칼 피어슨은 아버지와 아들의 키를 조사한 결과를 바탕으로 함수 관계를 도출하여 회귀분석 이론을 수학적으로 정립하였다. 회귀(regression)란?¶ 회귀를 설명하기 위해 먼저 위키백과에 정의된 회귀에 대한 설명을 살펴보겠습니다. 회귀(영어: regress 리그레스[*])의 원래 의미는 옛날 상태로 돌아가는 것을 의미한다. 영국의 유전학자..AI/RPA Developer
Table of Contents:

[머신러닝 완벽가이드] 회귀(Regression)와 경사하강법(Gradient Descent)

Article author: ai-creator.tistory.com
Reviews from users: 32380 Ratings
Top rated: 3.3
Lowest rated: 1
Summary of article content: Articles about [머신러닝 기초] 지도학습 – 선형 회귀(Regression) 분석 [머신러닝 기초] 지도학습 – 선형 회귀(Regression) 분석 … 머신러닝 회귀 알고리즘은 데이터를 계속 학습하면서 이 비용함수가 반환되는 값(=오류 … …
Most searched keywords: Whether you are looking for [머신러닝 기초] 지도학습 – 선형 회귀(Regression) 분석 [머신러닝 기초] 지도학습 – 선형 회귀(Regression) 분석 … 머신러닝 회귀 알고리즘은 데이터를 계속 학습하면서 이 비용함수가 반환되는 값(=오류 … ㅁ 선형 회귀란? 지도학습은 크게 2가지 유형으로 볼 수 있습니다. 1) 분류 2) 회귀 두가지 기법의 가장 큰 차이는 다음과 같다. 1) 분류 : 예측값이 이산형 클래스 값 2) 회귀 : 예측값이 연속형 숫자 값 데이..
Table of Contents:

ai-creator

[머신러닝 기초] 지도학습 – 선형 회귀(Regression) 분석 본문

ㅁ 선형 회귀란

ㅁ 단순 선형 회귀를 통한 회귀 이해

ㅁ 비용 최소화 하기 (경사하강법 Gradient Descent)

ㅁ 평가지표

ㅁ Sklearn API

ㅁ Regularization = 정규화 = 제약 (penalty)

ㅁ 그외 Sklearn API 에서 제공하는 선형 회귀 알고리즘

ㅁ 선형 회귀 모델을 위한 데이터 변환

ㅁ 추가학습

ㅁ 참고

티스토리툴바

[머신러닝 기초] 지도학습 - 선형 회귀(Regression) 분석 — [머신러닝 기초] 지도학습 – 선형 회귀(Regression) 분석

Article author: eusun0830.tistory.com
Reviews from users: 14746 Ratings
Top rated: 3.9
Lowest rated: 1
Summary of article content: Articles about 통계학의 선형회귀분석과 머신러닝의 Ridge, Lasso 회귀 모델 비교 :: Patience conquers the world Statistics modeling, Machine learning. 방정식 형태로 변수 간의 관계를 공식화함, 규칙 기반이 아닌 데이터에서 학습할 수 있는 알고리즘. …
Most searched keywords: Whether you are looking for 통계학의 선형회귀분석과 머신러닝의 Ridge, Lasso 회귀 모델 비교 :: Patience conquers the world Statistics modeling, Machine learning. 방정식 형태로 변수 간의 관계를 공식화함, 규칙 기반이 아닌 데이터에서 학습할 수 있는 알고리즘. 1. 통계학 모델링과 머신러닝 모델링의 주요 차이점 Statistics modeling Machine learning 방정식 형태로 변수 간의 관계를 공식화함 규칙 기반이 아닌 데이터에서 학습할 수 있는 알고리즘 데이터에 대한 모델..
Table of Contents:

인기포스트 MORE POST

1 통계학 모델링과 머신러닝 모델링의 주요 차이점

2 선형 모델의 가정

3 선형 회귀 모델링의 산업적 적용

4 선형 회귀 모델 예제

5 선형회귀 모델을 최상의 모델로 결정하기 위한 변수 추가 및 제거

TAG

회귀분석 기법의 5가지 일반 유형과 각각의 활용 방법

회귀분석은 데이터 분석에 사용되는 매우 강력한 머신러닝 도구이다. 어떻게 작동하는지, 주요 유형에는 어떤 것들이 있는지, 그리고 비즈니스에 어떤 도움을 주는지 알아보자.

머신러닝에서 회귀분석의 의미

회귀분석은 종속 변수(목표)와 하나 이상의 독립 변수(예측 변수라고도 함) 간의 미래 사건을 예측하는 방법이다. 예를 들면, 난폭운전과 운전자에 의한 교통사고 총 건수 사이의 상관관계를 예측하거나 비즈니스 상황에서는 특정 금액을 광고에 사용했을 때와 그것이 판매에 미치는 영향 사이의 관계를 예측하는 데 사용할 수 있다.

회귀분석은 머신러닝의 일반적인 모델 중 하나이다. 회귀분석 모델은 수치적 가치를 추정한다는 측면에서 관측치가 어느 범주에 속하는지를 식별하는 분류 모델과 다르다.

회귀분석은 예측, 시계열 모델링 및 변수 간 인과관계 발견 등에 주로 사용된다.

회귀분석이 중요한 이유

회귀분석은 실제 응용 프로그램에서 넓게 활용되고 있다. 연속 숫자를 포함하는 모든 머신러닝 문제 해결에 필수적이며, 여기에는 다음을 비롯한 많은 예가 포함된다:

금융 관련 예측(주택 가격 또는 주가)

판매 및 프로모션 예측

자동차 테스트

날씨 분석 및 예측

시계열 예측

회귀분석은 두 개 이상의 변수 사이에 유의미한 관계가 존재하는지 여부를 알려줄 뿐만 아니라 그 관계성에 대한 보다 구체적인 정보를 제공할 수 있다. 특히, 여러 변수가 종속 변수에 미치는 영향의 강도를 추정할 수 있다. 만약 한 변수(가령 가격)의 값을 변경하면 회귀분석을 통해 종속 변수(판매)에 어떤 영향을 미칠지 알 수 있다.

기업은 회귀분석을 사용하여 여러 척도로 측정된 변수의 효과를 검정할 수 있다. 활용할 수 있는 도구 상자에 회귀분석을 포함해두면, 예측 모델을 구축할 때 사용할 최상의 변수 집합을 평가하여 예측 정확도를 크게 높일 수 있다.

마지막으로 회귀분석은 데이터 모델링을 사용하여 머신러닝에서 회귀 문제를 해결하는 가장 좋은 방법이다. 차트에 데이터 포인트를 표시하고 이들을 관통하는 가장 적합한 선을 그어 각 데이터 포인트의 오류 가능성을 예측할 수 있다. 즉, 각 데이터 점이 선에서 멀리 떨어져 있을수록 예측 오차가 커진다(이 가장 적합한 선을 회귀선이라고 부르기도 한다).

회귀분석의 다양한 유형

1. 선형 회귀(Linear regression)

머신러닝에서 가장 일반적인 회귀분석 유형이라고 할 수 있는 선형 회귀는 예측 변수와 종속 변수로 구성되며, 이 둘은 선형 방식으로 서로 연관지어져 있다. 선형 회귀는 위에서 설명한 대로 가장 적합한 선, 즉 최적적합선을 사용한다.

변수들이 서로 선형적으로 연결되어 있는 경우 선형 회귀를 사용한다. 광고 지출 증가가 판매에 미치는 영향을 예측할 때 등이 예가 될 수 있다. 그러나 선형 회귀분석은 특이치에 영향을 받기 쉬우므로 빅데이터 집합을 분석하는 데 사용해서는 안 된다.

2. 로지스틱 회귀(Logistic regression)

종속 변수에 이산 값이 있는 경우, 다시 말해 0 또는 1, 참 또는 거짓, 흑 또는 백, 스팸 또는 스팸 아닌 것 등의 두 가지 값 중 하나만 취할 수 있는 경우 로지스틱 회귀를 사용하여 데이터를 분석할 수 있다.

로지스틱 회귀는 S자형 곡선을 사용하여 대상 변수와 독립 변수 사이의 관계를 표시한다. 그러나 로지스틱 회귀 분석 방식은 대상 변수에서 거의 동일한 값이 발생하는 대규모 데이터 세트에서 가장 효과가 있다는 사실에 유의해야 한다. 이 경우, 변수들의 순위를 지정할 때 문제를 일으킬 수 있기 때문에 서로 상관성이 높은 독립 변수들이 데이터 집합에 포함되어서는 안 된다. (이것은 multicollinearity, 즉 다중공선성이라고 알려진 현상으로, 회귀 분석에서 사용된 모델의 일부 예측 변수가 다른 예측 변수와 상관 정도가 높아, 데이터 분석 시 부정적인 영향을 미치는 현상을 의미한다.)

3. 리지 회귀(Ridge regression)

그러나, 불가피하게 독립 변수들 사이에 높은 상관 관계가 있는 경우라면 리지 회귀가 더 적합한 접근방식이다. 다중 회귀라고도 불리는 리지 회귀는 정규화 또는 규제화(regularization) 기법으로 알려져 있으며 모델의 복잡성을 줄이는 데 사용된다. 또한 ‘리지 회귀 페널티’로 알려진 약간의 편향, 즉 바이어스(bias)를 사용하여 모델이 과대적합(overfitting)에 덜 취약하게 만든다.

4. 라쏘 회귀(Lasso regression)

라쏘 회귀는 리지 회귀와 같이 모델의 복잡성을 줄여주는 또 다른 정규화 기법이다. 회귀 계수의 절대 사이즈를 금지함으로써 복잡성을 줄인다. 리지 회귀와는 다르게 아예 계수 값을 0에 가깝게 만든다.

그 장점은 기능 선택을 사용할 수 있다는 것이다. 데이터 집합에서 기능 세트를 선택하여 모델을 구축할 수 있다. 라쏘 회귀는 필요한 요소들만 사용하고 나머지를 0으로 설정함으로써 과대적합을 방지할 수 있다.

5. 다항 회귀(Polynomial regression)

다항 회귀는 선형 모델을 사용하여 비선형 데이터 집합을 모델링한다. 이것은 동그란 모양의 구멍에 네모난 모양의 못 또는 말뚝을 끼워 넣는 것과 같다. 다항 회귀는 독립 변수가 여러 개인 선형 회귀를 뜻하는 다중 선형 회귀와 비슷한 방식으로 작동하지만, 비선형 곡선을 사용한다. 즉, 데이터 포인트가 비선형 방식으로 존재할 때 사용한다.

모델은 이 데이터 포인트들을 지정된 수준의 다항식 특성으로 변환하고 선형 모델을 사용하여 모델화한다. 선형 회귀에서 볼 수 있는 직선이 아닌 곡선의 다항식 선을 사용하여 최적적합을 수행한다. 그러나 이 모델은 과대적합으로 나타나기 쉬우므로 이상한 결과치를 피하기 위해서는 끝 부분의 곡선을 분석하는 것이 좋다.

회귀 분석에는 위에서 소개한 것들보다 더 많은 종류가 있지만, 이 다섯 가지가 가장 일반적으로 사용되는 것들이다. 가장 적합한 모델을 선택하면 데이터가 가진 잠재력을 최대한 활용하여 더 큰 인사이트를 얻을 수 있다.

* 머신러닝을 사용하여 데이터를 실행 가능한 인사이트로 전환하는 방법에 대해 자세히 알아보고자 하시면 문의를 남겨주세요 . 애피어의 전문가 팀이 컨설팅을 제공해드립니다.

[머신러닝 이론] 회귀 (Regression)

728×90

회귀 소개

회귀는 현대 통계학을 떠받치고 있는 주요 기둥 중 하나이다. 회귀 기반의 분석은 엔지니어링, 의학, 사회과학, 경제학 등의 분야가 발전하는 데 크게 기여해왔다. 회귀 분석은 유전적 특성을 연구하던 영국의 통계학자 갈톤(Galton)이 수행한 연구에서 유래했다는 것이 일반론이다. 부모와 자식 간의 키의 상관관계를 분석했던 갈톤은 부모의 키가 모두 클 때 자식의 키가 크긴 하지만 그렇다고 부모를 능가할 정도로 크지 않았고, 부모의 키가 모두 아주 작을 때 그 자식의 키가 작기는 하지만 부모보다는 큰 경향을 발견했다. 부모의 키가 아주 크더라도 자식의 키가 부모보다 더 커서 세대를 이어가면서 무한정 커지는(발산) 것은 아니며, 부모의 키가 아주 작더라도 자식의 키가 부모보다 더 작아서 세대를 이어가며 무한정 작아지는(수렴) 것이 아니라는 것이다. 즉, 사람의 키는 평균 키로 회귀하려는 경향을 가진다는 자연의 법칙이 있다는 것이다.

회귀는 여러 개의 독립변수와 한 개의 종속변수 간의 상관관계를 모델링하는 기법을 통칭한다. 예를 들어 아파트의 방 개수, 방 크기, 주변 학군 등 여러 개의 독립변수에 따라 아파트 가격이라는 종속변수가 어떤 관계를 나타내는지를 모델링하고 예측하는 것이다. $Y = W_1 * X_1 + W_2 * X_2 + W_3 * X_3 + \dots + W_n * X_n$이라는 선형 회귀식을 예로 들면 $Y$는 종속변수, 즉 아파트 가격을 뜻한다. 그리고 $X_1, X_2, X_3, \dots, X_n$은 방 개수, 방 크기, 주변 학군 등의 독립변수를 의미한다. 그리고 $X_1, X_2, X_3, \dots, X_n$은 독립변수의 값에 영향을 미치는 회귀 계수(Regression coefficients)이다. 머신러닝 관점에서 보면 독립변수는 피처에 해당되며 종속변수는 결정 값이다. 머신러닝 회귀 예측의 핵심은 주어진 피처와 결정 값 데이터 기반에서 학습을 통해 최적의 회귀 계수를 찾아내는 것이다.

회귀는 회귀 계수의 선형/비선형 여부, 독립변수의 개수, 종속변수의 개수에 따라 여러가지 유형으로 나눌 수 있다. 회귀에서 가장 중요한 것은 회귀 계수이며, 이 회귀 계수가 선형인지 아닌지에 따라 선형 회귀와 비선형 회귀로 나눌 수 있다. 그리고 독립변수의 개수가 한 개인지 여러 개인지에 따라 단일 회귀, 다중 회귀로 나뉜다.

지도학습은 크게 분류와 회귀로 나뉜다. 이 두 기법의 가장 큰 차이는 분류는 예측값이 카테고리와 같은 이산형 클래스 값이고, 회귀는 연속형 숫자 값이라는 것이다.

여러 가지 회귀 중에서 선형 회귀가 가장 많이 사용된다. 선형 회귀는 실제 값과 예측값의 차이(오류의 제곱 값)를 최소화하는 직선형 회귀선을 최적화하는 방식이다. 선형 회귀 모델은 규제(Regularization) 방법에 따라 다시 별도의 유형으로 나뉠 수 있다. 규제는 일반적인 선형 회귀의 과적합 문제를 해결하기 위해서 회귀 계수에 패널티 값을 적용하는 것을 말한다. 대표적인 선형 회귀 모델은 다음과 같다.

선형 회귀 모델

일반 선형 회귀 : 예측값과 실제값의 RSS(Residual Sum of Squares)를 최소화할 수 있도록 회귀 계수를 최적화하며, 규제(Regularization)를 적용하지 않은 모델이다.

릿지(Ridge) : 릿지 회귀는 선형 회귀에 L2 규제를 추가한 회귀 모델이다. 릿지 회귀는 L2 규제를 적용하는데, L2 규제는 상대적으로 큰 회귀 계수 값의 예측 영향도를 감소시키기 위해서 회귀 계수값을 더 작게 만드는 규제 모델이다.

라쏘(Lasso) : 라쏘 회귀는 선형 회귀에 L1 규제를 적용한 방식이다. L2 규제가 회귀 계수 값의 크기를 줄이는 데 반해, L1 규제는 예측 영향력이 적은 피처의 회귀 계수를 0으로 만들어 회귀 예측 시 피처가 선택되지 않게 하는 것이다. 이러한 특성 때문에 L1 규제는 피처 선택 기능으로도 불린다.

엘라스틱넷(LeasticNet) : L2, L1 규제를 함께 결합한 모델이다. 주로 피처가 많은 데이터 셋에서 적용되며, L1 규제로 피처의 개수를 줄임과 동시에 L2 규제로 계수 값의 크기를 조정한다.

로지스틱 회귀(Logistic Regression) : 로지스틱 회귀는 회귀라는 이름이 붙어 있지만, 사실은 분류에 사용되는 선형 모델이다. 로지스틱 회귀는 매우 강력한 분류 알고리즘이다. 일반적으로 이진 분류뿐만 아니라 희소 영역의 분류, 예를 들어 텍스트 분류와 같은 영역에서 뛰어난 예측 성능을 보인다.

단순 선형 회귀를 통한 회귀 이해

단순 선형 회귀는 독립변수도 하나, 종속변수도 하나인 선형 회귀이다. 예를 들어, 주택 가격이 주택의 크기로만 결정된다고 하면 2차원 평면에 직선(선형)형태의 관계로 표현할 수 있다. $X$축이 주택의 크기이고, $Y$축이 가격이라할 경우 1차 함수식으로 모델링할 수 있다.

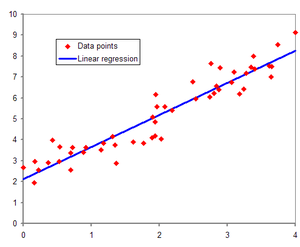
$\hat{Y} = \omega_0 + \omega_1 * X$

위 설명의 모델링과는 별개로 선형 회귀 모델을 보이기 위한 자료

독립 변수가 1개인 단순 선형 회귀에서는 기울기인 $\omega_1$과 절편인 $\omega_0$을 회귀 계수로 지칭한다. 위와 같은 1차 함수로 모델링했다면 실제 주택 가격은 이러한 1차 함수 값에서 실제 값만큼의 오류 값을 빼거나 더한 값이 된다.

이렇게 실제값과 회귀 모델의 차이에 따른 오류값을 남은 오류, 즉 잔차라 부른다. 최적의 회귀 모델을 만든다는 것은 전체 데이터의 잔차(오류값) 합이 최소가 되는 모델을 만든다는 의미이며, 동시에 오류값 합이 최소가 될 수 있는 최적의 회귀 계수를 찾는다는 의미이다.

오류값은 +나 -가 될 수 있기에 전체 데이터의 오류합을 구하기 위해 단순히 더할경우 뜻하지 않게 오류합이 줄어들 수 있다. 따라서 보통 오류합을 계산할 때는 절대값을 취해서 더하거나, 오류값의 제곱을 구해서 더하는 방식(RSS, Residual Sum of Square)를 취한다. 일반적으로 미분 등의 계산을 편리하게 하기 위해서 RSS(Residual Sum of Square) 방식으로 오류합을 구한다. 즉, $Error^2 = RSS$이다.

$RSS$는 이제 변수가 $\omega_0, \omega_1$인 식으로 표현할 수 있으며, 이 $RSS$를 최소로 하는 $\omega_0, \omega_1$, 즉 회귀 계수를 학습을 통해서 찾는 것이 머신러닝 기반 회귀의 핵심 사항이다. $RSS$는 회귀식의 독립변수 $X$, 종속변수 $Y$가 중심 변수가 아니라 $\omega$ 변수(회귀 계수)가 중심 변수임을 인지하는 것이 매우 중요하다(학습 데이터로 입력되는 독립변수와 종속변수는 $RSS$에서 모두 상수로 간주한다. 일반적으로 $RSS$는 학습 데이터의 건수로 나누어서 다음과 같이 정규화된 식으로 표현된다.

$RSS(\omega_0,\omega_1) =$ $1 \over N$ $\sum_{i=1}^N (y_i – (\omega_0 + \omega_1 * x_i))^2$

회귀에서 $RSS$는 비용(Cost)이며 $\omega$ 변수(회귀 계수)로 구성되는 $RSS$를 비용 함수라고 한다. 머신러닝 회귀 알고리즘은 데이터를 계속 학습하면서 이 비용 함수가 반환하는 값(즉, 오류값)을 지속해서 감소시키고 최종적으로는 더 이상 감소하지 않는 최소의 오류값을 구하는 것이다. 비용 함수를 손실 함수(loss function)라고도 한다.

회귀 평가 지표

회귀의 평가를 위한 지표는 실제값과 회귀 예측값의 차이값을 기반으로 한 지표가 중심이다. 실제값과 예측값의 차이를 단순히 더하면 +와 -가 섞여서 오류가 상쇄된다. 예를 들어 데이터 두 개의 예측 차이가 하나는 -3, 다른 하나는 +3일 경우 단순히 더하면 오류가 0으로 나타나기 때문에 정확한 지표가 될 수 없다. 따라서 오류의 절대값 평균이나 제곱, 또는 제곱한 뒤 다시 루트를 씌운 평균값을 구한다. 일반적으로 회귀의 성능을 평가하는 지표는 다음과 같다.

평가 지표 설명 수식 MAE Mean Absolute Error이며 실제값과 예측값의 차이를 절대값으로 변환해 평균한 것 $MAE = $ $1 \over n$ $\sum_{i=1}^n |Yi – \hat{Y}i|$ MSE Mean Squared Error이며 실제값과 예측값의 차이를 제곱해 평균한 것 $MSE = $ $1 \over n$ $\sum_{i=1}^n (Yi – \hat{Y}i)^2$ RMSE MSE 값은 오류의 제곱을 구하므로 실제 오류 평균보다 더 커지는 특성이 있으므로 MSE에 루트를 씌운 것이 RMSE. $RMSE = $ $\sqrt {{1 \over n} \sum_{i=1}^n (Yi – \hat{Y}i)^2}$ $R^2$ 분산 기반으로 예측 성능을 평가한다. 실제값의 분산 대비 예측값의 분산 비율을 지표로 하며, 1에 가까울수록 예측 정확도가 높음 $R^2 = {예측값 Variacne \over 실제값 Variance}$

이외에도 MSE나 RMSE에 로그를 적용한 MSLE(Mean Squared Log Error)와 RMSLE(Root Mean Squared Log Error)도 사용한다. 사이킷런은 RMSE를 제공하지 않는다. 따라서 RMSE를 구하기 위해서는 MSE에 제곱근을 씌워서 계산하는 함수를 직접 만들어야 한다. 다음은 각 평가 방법에 대한 사이킷런의 API 및 cross_val_score나 GridSearchCV에서 평가 시 사용되는 scoring 파라미터의 적용값이다.

평가 방법 사이킷런 평가 지표 API Scoring 함수 적용 값 MAE metrics.meam_absoulte_error ‘neg_mean_absolute_error’ MSE metrics.mean_squared_error ‘neg_mean_squared_error’ $R^2$ metrics.r2_score ‘r2’

Reference
[1] 파이썬 머신러닝 완벽가이드
[2] https://ko.wikipedia.org/wiki/회귀_분석

선형 회귀(Regression) 분석

반응형

ㅁ 선형 회귀란?

지도학습은 크게 2가지 유형으로 볼 수 있습니다.

1) 분류

2) 회귀

두가지 기법의 가장 큰 차이는 다음과 같다.

1) 분류 : 예측값이 이산형 클래스 값

2) 회귀 : 예측값이 연속형 숫자 값

데이터를 가장 잘 설명하는 최적의 회귀식를 찾는다.

회귀는 여러개의 독립변수(x)와 한개의 종속변수(y)의 상관관계를 모델링하는 기법 을 통칭한다.

w0, w1, w2…. 를 회귀계수(regression coefficients)라고하며, 회귀 예측의 핵습은 주어진 피쳐(x, input, 독립변수)와 결정값(y, output, 종속변수)값 기반에서 학습을 통해 최적의 회귀계수를 찾아내는 것 이다.

독립변수 1개 단일 회귀 독립변수 여러개 다중 회귀 회귀계수의 결합 선형 선형회귀 회귀계수의 결합 비선형 비선형 회귀

단일 회귀 vs 다중회귀

ㅁ 단순 선형 회귀를 통한 회귀 이해

단순 선형 회귀는

– 독립변수 1개

– 종속변수 1개

인 선형 회귀 이다.

독립변수가 1개인 단순 선형 회귀에서는 기울기 w1과 절편 w0를 회귀계수로 칭하빈다. (절편은 영어로 intercept)

“데이터를 가장 잘 설명하는”이라는 의미는 “실제값과 예측차이가 작은” 으로 표현할 수 있습니다.

즉, 최적의 회귀 모델을 만든다는 것? “전체 데이터의 잔차(오류값) 합이 최소가 되는 모델을 만든다” 라는 의미입니다.

잔차(오류값) 합을 구하는 방법은 2가지를 사용하는데,

1) MAE (Mean Absolute Error) : 절대값을 취하는 방법

2) RSS (Residual Sum of Square) : 제곱을 취하는 방법

일반적으로 미분등의 계산이 편리하여 RSS를 사용 한다.

다양한 표기법

RSS를 최소 로하는 w0, w1, 즉 회귀계수를 학습을 통해서 찾는 것 이 머신러닝 기반 회귀의 핵심사항이다.

회귀에서는 이 RSS는 비용(Cost)이며, w변수(회귀계수)로 구성된 RSS를 비용함수(cost function, loss function, 손실함수) 라고 한다. 머신러닝 회귀 알고리즘은 데이터를 계속 학습하면서 이 비용함수가 반환되는 값(=오류값)을 지속해서 감소시키고, 더이상 감소하지 않는 최소의 오류값 을 구하는 것이다.

ㅁ 비용 최소화 하기 (경사하강법, Gradient Descent)

어떻게 비용함수가 최소가 되는 W 파라미터를 구할 수 있을까?

예시로 x = [1,2,3] 이라고 하고, y=[3,5,7]의 관측값이 있다고 했을때 우리는 f(x) = 2x+1 이라고 생각할 수 있다. 하지만, 기계는 이렇게 계산을 할 수 없다. 초기화된 값을 기준으로 점점 오류가 작아지는 방향으로 f(x)식을 완성 해 갑니다.

오류값과 관련된 RSS를 비용함수(cost function, loss)이라고 하며, 비용함수가 최소화할 수 있는 회귀계수(w)를 찾는다(=최적화합니다). 즉, ‘점진적으로’ 반복적인 계산을 통해 W파라메터 값을 업데이트 하면서 오류값이 최소가 되는 W파라메터를 구하는 것 이다.

경사하강법(Gradient Descent)을 통해 최적의 W를 찾아낸다.

이 동작은 마치 깜깜한 밤, 산 정상에서 내려가야 한다고 가정했을 때, 여러분들이 하는 일과 비슷하게 동작한다.

앞이 보이지 않기 때문에 스스로에게 질문을 던질 것이다.

Step1) 다 내려왔습니까?

Step2) 어느 방향으로 가야 하나요? 아래로 내려가세요

Step3) 얼만큼 가야 하나요? 답을 말해줄 수 없음, 즉, 적당히 가세요

Step4) 조금 움직인다.

를 반복적으로 수행할 것이다.

경사하강법도 최적의 W를 찾기 위해 아래 행위를 반복하게 된다.

Step1) 다 내려왔습니까? = Gradient가 0입니까? => YES / NO

Step2) 어느 방향으로 가야 하나요? = 아래로 내려가세요

Step3) 얼만큼 가야 하나요? 답을 말해줄 수 없음, 즉, 적당히 가세요 = learning rate

Step4) 조금 움직인다. = W를 업데이트 한다.

<<경사하강법 상세>>

더보기 출처 : https://www.youtube.com/watch?v=ve6gtpZV83E 출처 : https://www.youtube.com/watch?v=ve6gtpZV83E <미분 기초> <편미분이란?> 다변수 함수의 특정 변수를 제외한 나머지 변수를 상수로 생각하여 미분 하는 것이다. 출처 : https://www.youtube.com/watch?v=ve6gtpZV83E

ㅁ 평가지표

평가지표 설명 수식 MAE Mean Absoulute Error(MAE)이며 실제값과 예측값의 치이를 절댓값으로 변환해 평균한 것 MSE Mean Squared Error(MSE)이며 실제값과 예측값의 차이를 제곱으로 평균한 것 MSLE Mean Squared Log Error(MSLE)이며, MSE에 로그를 적용한 것이다. 결정값이 클수록 오류값도 커지기 때문에 일부 큰 오류값들로 인해 전체 오류값이 커지는 것을 막아줌

ex) 주택가격 log(MSE) RMSE MSE값은 오류의 제곱을 구하므로 실제 오류 평균보다 더 커지는 특성이 있음.

RMSE(Root Mean Squared Error)는 MSE에 루트를 씌운 것 RMSLE Root Mean Squared Log Error(RMSLE)이며, RMSE에 로그를 적용한 것이다. 결정값이 클수록 오류값도 커지기 때문에 일부 큰 오류값들로 인해 전체 오류값이 커지는 것을 막아줌

ex) 주택가격 log(RMSE) R^2 분산 기반으로 예측 성능을 평가

실제 값의 분산 대비 예측값의 분산 비율(1에 가까울수록 예측 정확도 높음)

ㅁ Sklearn API

이를 위해 sklearn에서는 API를 지원한다.

목적 import API LinearRegression from sklearn.linear_model import LinearRegression LinearRegression()

– coef_

– intercept_ MAE from sklearn.metrics import mean_absolute_error mean_absolute_error() MSE from sklearn.metrics import mean_squared_error mean_squared_error() RMSE ** 제공하지 않음

MSE에 제곱근을 씌워서 계산하는 함수를 직접 만들어야 한다. R^2 from sklearn.metrics import r2_score r2_score()

코드에서 보면,

from sklearn.model_selection import train_test_split from sklearn.linear_model import LinearRegression from sklearn.metrics import mean_squared_error , r2_score import numpy as np import matplotlib.pyplot as plt import pandas as pd import seaborn as sns from scipy import stats from sklearn.datasets import load_boston %matplotlib inline # boston 데이타셋 로드 boston = load_boston() # boston 데이타셋 DataFrame 변환 bostonDF = pd.DataFrame(boston.data , columns = boston.feature_names) # boston dataset의 target array는 주택 가격임. 이를 PRICE 컬럼으로 DataFrame에 추가함. bostonDF[‘PRICE’] = boston.target print(‘Boston 데이타셋 크기 :’,bostonDF.shape) bostonDF.head() y_target = bostonDF[‘PRICE’] X_data = bostonDF.drop([‘PRICE’],axis=1,inplace=False) X_train , X_test , y_train , y_test = train_test_split(X_data , y_target ,test_size=0.3, random_state=156) # Linear Regression OLS로 학습/예측/평가 수행. lr = LinearRegression() lr.fit(X_train ,y_train ) y_preds = lr.predict(X_test) mse = mean_squared_error(y_test, y_preds) rmse = np.sqrt(mse) print(‘MSE : {0:.3f} , RMSE : {1:.3F}’.format(mse , rmse)) print(‘Variance score : {0:.3f}’.format(r2_score(y_test, y_preds))) print(‘절편 값:’,lr.intercept_) print(‘회귀 계수값:’, np.round(lr.coef_, 1))

결과값

MSE : 17.297 , RMSE : 4.159

Variance score : 0.757

절편 값: 40.995595172164336

회귀 계수값: [ -0.1 0.1 0. 3. -19.8 3.4 0. -1.7 0.4 -0. -0.9 0. -0.6]
ㅁ Regularization = 정규화 = 제약 (penalty)

현실 데이터는 사람이 어찌할 수 없는 noise가 항상 존재하고 있다.

그러나, 잔차의 경우는 train data에 대해서만 고려한 오류입니다. train data에 해당하는 잔차를 줄이기 위해서는 복잡한 회귀식이 도출되면 됩니다. 그러나, 복잡한 회귀식으로 train data에 과적합되면 될수록 실제데이터에서는 예측력이 떨어지는 현상이 발생하게 된다.

Overfitting 은 학습데이터에 너무 최적화되어 W 값이 잡히고, 이후 학습 데이터가 아닌 새로운 데이터에는 올바른 값을 내보내지 못하는 현상을 의미한다. 즉, 현재 주어진 데이터(학습데이터)에 너무 과적합되어 모델(W) 이 피팅되었으니, 이를 좀 덜 적합하게하고, 이후 새로운 데이터에도 일반적으로 들어맞는 모델을 만들어야 한다. 이 때, 과적합이 아닌 일반성을 띄게 해주는 기법을 Regularization 이라고 한다.

즉, 오버피팅을 줄기위해 약간의 규제(penalty)를 주는 방법을 고민하게 되었다. 우리가 조정할 수 있는 것은 W값, 즉 각 x에 대한 계수 값이다.

Regularization의 목적은 반복적으로 발생하는 cost에 영향을 미치는 w(weight)가 보다 적은 영향을 미치도록 조정해주는 역할을 한다. Regularization에는 자주 비교되는 L1 Regularization과 L2 Regularization가 있으며, L1 Regularization보다는 L2 Regularization를 일반적으로 더 많이 사용함

출처 : https://youtu.be/pJCcGK5omhE 제약의 유무 (출처 : https://youtu.be/pJCcGK5omhE)

1) L1 Regularization

– W의 절대값에 패널티를 부여하는 방식

– 영향력이 크지 않는 회귀계수값을 0으로 변환 = feature selection 기능

– Lasso 회귀

– alpha는 하이퍼파라메터

참고) L1 Norm

2) L2 Regularization

– W의 제곱에 패널티를 부여하는 방식

– 회귀계수의 크기를 감소시킴

– Ridge 회귀

참고) L2 Norm

3) L1+L2 Regularization

– L1과 L2의 패널티를 섞음

– ElasticNet 회귀

Lasso / Lidge / ElasticNet의 회귀계수 변화

4) Sklearn API

이를 위해 sklearn에서는 API를 지원한다.

목적 import API Lasso from sklearn.linear_model import Lasso Lasso()

– coef_

– intercept_ Ridge from sklearn.linear_model import Ridge Ridge() ElasticNet from sklearn.linear_model import ElasticNet ElasticNet()

– l1_ratio == 0 이면, L2 규제와 동일

– l1_ratio == 1 이면, L1 규제와 동일

코드에서 보면,

# alpha값에 따른 회귀 모델의 폴드 평균 RMSE를 출력하고 회귀 계수값들을 DataFrame으로 반환 def get_linear_reg_eval(model_name, params=None, X_data_n=None, y_target_n=None, verbose=True, return_coeff=True): coeff_df = pd.DataFrame() if verbose : print(‘####### ‘, model_name , ‘#######’) for param in params: if model_name ==’Ridge’: model = Ridge(alpha=param) elif model_name ==’Lasso’: model = Lasso(alpha=param) elif model_name ==’ElasticNet’: model = ElasticNet(alpha=param, l1_ratio=0.7) neg_mse_scores = cross_val_score(model, X_data_n, y_target_n, scoring=”neg_mean_squared_error”, cv = 5) avg_rmse = np.mean(np.sqrt(-1 * neg_mse_scores)) print(‘alpha {0}일 때 5 폴드 세트의 평균 RMSE: {1:.3f} ‘.format(param, avg_rmse)) # cross_val_score는 evaluation metric만 반환하므로 모델을 다시 학습하여 회귀 계수 추출 model.fit(X_data_n , y_target_n) if return_coeff: # alpha에 따른 피처별 회귀 계수를 Series로 변환하고 이를 DataFrame의 컬럼으로 추가. coeff = pd.Series(data=model.coef_ , index=X_data_n.columns ) colname=’alpha:’+str(param) coeff_df[colname] = coeff return coeff_df # end of get_linear_regre_eval # 라쏘에 사용될 alpha 파라미터의 값들을 정의하고 get_linear_reg_eval() 함수 호출 lasso_alphas = [ 0.07, 0.1, 0.5, 1, 3] coeff_lasso_df =get_linear_reg_eval(‘Lasso’, params=lasso_alphas, X_data_n=X_data, y_target_n=y_target)

ㅁ 그외 Sklearn API 에서 제공하는 선형 회귀 알고리즘

목적 import API 의사결정나무 from sklearn.tree import DecisionTreeRegressor

DecisionTreeRegressor() 랜덤포레스트 from sklearn.ensemble import RandomForestRegressor RandomForestRegressor() XGBoost from xgboost import XGBRegressor XGBRegressor() LightGBM from lightgbm import LGBMRegressor LGBMRegressor()

코드에서 보면,

from sklearn.tree import DecisionTreeRegressor from sklearn.ensemble import GradientBoostingRegressor from xgboost import XGBRegressor from lightgbm import LGBMRegressor from sklearn.model_selection import cross_val_score def get_model_cv_prediction(model, X_data, y_target): neg_mse_scores = cross_val_score(model, X_data, y_target, scoring=”neg_mean_squared_error”, cv = 5) rmse_scores = np.sqrt(-1 * neg_mse_scores) avg_rmse = np.mean(rmse_scores) print(‘##### ‘,model.__class__.__name__ , ‘ #####’) print(‘ 5 교차 검증의 평균 RMSE : {0:.3f} ‘.format(avg_rmse)) dt_reg = DecisionTreeRegressor(random_state=0, max_depth=4) rf_reg = RandomForestRegressor(random_state=0, n_estimators=1000) xgb_reg = XGBRegressor(n_estimators=1000) lgb_reg = LGBMRegressor(n_estimators=1000) # 트리 기반의 회귀 모델을 반복하면서 평가 수행 models = [dt_reg, rf_reg, xgb_reg, lgb_reg] for model in models: get_model_cv_prediction(model, X_data, y_target)

ㅁ 선형 회귀 모델을 위한 데이터 변환

– 선형모델은 일반적으로 피처와 타깃값 간에 선형의 관계 가 있다고 가정한다

– 선형회귀 모델은 피처값과 타깃값의 분포가 정규분포 형태를 매우 선호 한다. 특히 타깃값(y)의 경우 정규분포가 아니라 특정값의 분포가 치우친 왜곡(skew)된 형태의 분포도일 경우 예측성능에 부정적인 영향을 미칠 가능성이 높다.

– 선형 회귀 모델을 적용하기 전에 먼저 데이터에 대한 스케일링/정규화 작업 을 수행하는 것이 일반적

피쳐데이터(x) case1) StandardScaler 클래스를 이용해 평균 0, 분산 1인 표준 정규분포를 가진 데이터 세트로 변환

case2) MinMaxScaler 클래스를 이용해 최솟값이 0이고, 최댓값이 1인 값으로 정규화를 수행

case3) log 변환

case4) categorical variable은 label encoding이 아닌 one-hot encoding 수행 타깃값(y) 일반적으로 log변환

-> log(0)는 무한대값이 되므로, log(관측값+1)에 해당하는 numpy.log1p() 를 사용

-> 예측값은 log1p()를 적용하여 예측한 것으므로, 최종예측값은 numpy.expm1() 을 적용해야 한다.

왜곡(skew)된 형태의 분포도 / log 변환 후 정규분포 형태

from sklearn.preprocessing import StandardScaler, MinMaxScaler # method는 표준 정규 분포 변환(Standard), 최대값/최소값 정규화(MinMax), 로그변환(Log) 결정 def get_scaled_data(method=’None’, input_data=None): if method == ‘Standard’: scaled_data = StandardScaler().fit_transform(input_data) elif method == ‘MinMax’: scaled_data = MinMaxScaler().fit_transform(input_data) elif method == ‘Log’: scaled_data = np.log1p(input_data) else: scaled_data = input_data return scaled_data

ㅁ 추가학습

– 자전거 수요예측 (Link)

– 주택가격예측 (Link), 데이터 다운로드 (Link)

ㅁ 참고

https://ratsgo.github.io/machine%20learning/2017/05/22/RLR/

– [책] 파이썬 머신러닝 완벽가이드

– [블로그] 파이썬 머신러닝 완벽가이드 정리본 (Link)

– [소스코드 출처] : https://github.com/wikibook/pymldg-rev

반응형

So you have finished reading the 머신 러닝 회귀 분석 topic article, if you find this article useful, please share it. Thank you very much. See more: 머신러닝 회귀분석 차이, 머신러닝 회귀분석 예제, 머신러닝 회귀 알고리즘, 머신러닝 다중회귀분석, 회귀분석 데이터셋, 머신러닝 회귀 모델, 머신러닝 회귀 알고리즘 종류, 머신러닝 회귀란

Top 17 머신 러닝 회귀 분석 The 43 New Answer

머신 러닝 회귀 분석

회귀 (Regression)란?

회귀분석 기법의 5가지 일반 유형과 각각의 활용 방법

[머신러닝 이론] 회귀 (Regression) :: For a better world.

[머신러닝 완벽가이드] 회귀(Regression)와 경사하강법(Gradient Descent)

[머신러닝 기초] 지도학습 – 선형 회귀(Regression) 분석

통계학의 선형회귀분석과 머신러닝의 Ridge, Lasso 회귀 모델 비교 :: Patience conquers the world

03) 선형 회귀(Linear Regression) – 딥 러닝을 이용한 자연어 처리 입문

[머신러닝] 회귀(Regression) 알고리즘

[논문]다중회귀분석과 머신러닝 기법을 이용한 호우피해 예측함수 개발

회귀분석 기법의 5가지 일반 유형과 각각의 활용 방법

[머신러닝 이론] 회귀 (Regression)

선형 회귀(Regression) 분석

Leave a Comment Cancel reply