Top 43 푸리에 변환 그래프 The 35 Correct Answer

You are looking for information, articles, knowledge about the topic nail salons open on sunday near me 푸리에 변환 그래프 on Google, you do not find the information you need! Here are the best content compiled and compiled by the Chewathai27.com/to team, along with other related topics such as: 푸리에 변환 그래프 푸리에 변환 고등학교, 푸리에 변환 사이트, 푸리에 변환 예제, 푸리에 변환 프로그램, 푸리에 변환 공식 표, 푸리에 변환 풀이, 푸리에 변환 미분, 푸리에 변환 유도

푸리에 변환.. 왔습니다. 그려서 보여드리겠습니다.

05-2. 한 신호를 정해서 손으로 푸리에 변환 해보기

Article author: infograph.tistory.com
Reviews from users: 17265 Ratings
Top rated: 4.2
Lowest rated: 1
Summary of article content: Articles about 05-2. 한 신호를 정해서 손으로 푸리에 변환 해보기 Updating …
Most searched keywords: Whether you are looking for 05-2. 한 신호를 정해서 손으로 푸리에 변환 해보기 Updating 간단한 신호(시간에 대한 크기 값으로 주어지는)에 대해서 푸리에 변환을 해보자. 직접 손으로 한 번 풀어봐야, 푸리에 변환식의 의미를 체감하게 될 것이다. 푸리에 변환식에는 적분이 들어가 있어서, 신호가 조..
Table of Contents:

‘푸리에 변환 신호푸리에 변환의 모든 것’ Related Articles

티스토리툴바

Article author: gosamy.tistory.com
Reviews from users: 7048 Ratings
Top rated: 3.7
Lowest rated: 1
Summary of article content: Articles about 푸리에 변환에 대한 정확한 분석(Fourier Transform) Updating …
Most searched keywords: Whether you are looking for 푸리에 변환에 대한 정확한 분석(Fourier Transform) Updating 푸리에 급수 다음 등장하는 푸리에 변환은 적분변환(Integral Transform) 의 알파이자 오메가입니다. 대학에서 수학을 사용하는 학과에서 배우지 않을 수 없는 개념이고, 활용도는 무궁무진합니다. 변환이라는 특..
Table of Contents:

함수 $f(x)$ 에 대한 푸리에 변환식은 다음과 같다 ($f$는 주기함수가 아니어도 된다)$$f(x)=frac{1}{sqrt{2pi}}int_{-infty}^{infty}g(omega)e^{displaystyle iomega x}domega$$ $$g(omega)=frac{1}{sqrt{2pi}} int_{-infty}^{infty}f(x)e^{displaystyle -iomega x}dx$$여기서 두 식의 우변 가장 앞에 붙은 계수를 각각 $AB$라 하면 $AB=displaystylefrac{1}{2pi}$ 가 되도록 나누어 붙일 수 있다 위와 같이 각각 $displaystylefrac{1}{sqrt{2pi}}$ 을 취하는 것이 보편적이다

공지사항

최근글

05-2. 한 신호를 정해서 손으로 푸리에 변환 해보기

반응형

간단한 신호(시간에 대한 크기 값으로 주어지는)에 대해서 푸리에 변환을 해보자. 직접 손으로 한 번 풀어봐야, 푸리에 변환식의 의미를 체감하게 될 것이다.

푸리에 변환식에는 적분이 들어가 있어서, 신호가 조금만 복잡해도 손으로 풀기 어렵다. 해서, 가장 단순한 신호를 가지고 계산해보자.

가장 단순한 신호. 계속해서 1의 값을 가지는 신호를 대상으로 하자.

시간에 대한 그래프로 그려보면 아래와 같이 될 것이다.

(그림 1) 시간에 대한 신호 그래프

이러한 신호에 대한 주파수 영역에서의 그래프는 어떻게 될까?

시간이 변함에 따라 신호 값의 변화가 없이 계속 1이다. 즉, 시간에 대한 변화값이 없다는 것은 주기가 무한대라는 얘기이고, 주파수는 0이라는 것.

따라서, 주파수가 0인 부분에서만 값이 존재하게 될 것이다.

(그림 2) 주파수에 대한 그래프

이제 (그림 1)과 같은 신호에 대해 푸리에 변환을 해서, 진짜 (그림 2)와 같은 변환이 되는지 확인해 보자.

푸리에 변환식을 다시 적어본다.

$$ Y(f)= \int _{-\infty} ^{\infty} {f(t)e^{-i2\pi ft}dt} \tag {1}$$

흠… 문제는 적분의 범위가 $-\infty$ ~ $\infty$이다. 무한대에 대한 계산을 할 수 없다.

그렇다면, 계산이 가능하게 하기 위해 임의로 시간의 범위 $\Delta t$를 정해보자. (일단 계산 가능한 범위를 정해서 계산해보고, 이 $\Delta t$를 점점 더 커지게 해서 무한대까지 키우는 걸로 해보는 게 풀이 전략)

$\Delta t$의 범위를 0을 중심으로 좌우 대칭이 되게 하자. 그래야 계산이 편할 것이다. 범위는 $-\dfrac {\Delta t}{2}$ ~ $\dfrac {\Delta t}{2}$

(그림 3)

이렇게하면, $t < -\dfrac{\Delta t}{2}$와 $t > \dfrac {\Delta t}{2}$의 영역에서는 신호 값이 없고(=신호 값이 0이고), $-\dfrac {\Delta t}{2}$와 $\dfrac {\Delta t}{2}$ 사이에서만 값이 존재하게 된다. 따라서, 이를 그래프로 다시 그려보면 아래와 같은 모습이 된다.

(그림 4)

이제 (그림 4)와 같은 신호를, 식 (1)을 이용해서 푸리에 변환 해보자.

적분의 범위는 $-\dfrac {\Delta t}{2}$와 $\dfrac {\Delta t}{2}$ 사이만 될 것이다. 그 이외의 범위에서는 값이 $0$이기 때문이다. 그리고, $y(t)$의 값은 $1$이다.

이제 식 (1)을 다시 써보면,

$$ \begin{align} Y(f) &= \int _{-\frac {\Delta t}{2}} ^{\frac {\Delta t}{2}} {1 \cdot e^{-i2\pi ft}}dt \\ &= \left [ \dfrac{-1}{i2\pi f} e^{-i2\pi ft} \right ]^{\frac {\Delta t}{2}} _{-\frac{\Delta t}{2}}\\ &= – \dfrac {1}{i2\pi f}\left ( e^{-i2\pi f\cdot \frac {\Delta t}{2}}-e^{-i2\pi f \cdot \frac {-\Delta t}{2}} \right ) \\ &= – \dfrac {1}{i2\pi f} ( e^{-i\pi f\cdot \Delta t}-e^{i\pi f \cdot \Delta t} ) \\ &=\dfrac {1}{i2\pi f} (e^{i\pi f \cdot \Delta t} -e^{-i\pi f \cdot \Delta t}) \end{align} \tag {2}$$

여기서 지수함수의 적분 방법이 쓰였는데, 적분 공식은 아래와 같다. 아래 식에서 $a$는 식 (2)에서는 $-i2\pi f$인 것이다.

$$ \int {e^{ax}}dx = \dfrac{1}{a} e^{ax} \tag {지수함수의 적분 공식}$$

푸리에 변환을 해봤더니 식 (2)가 나왔다. 아직 이 식을 가지고 어떤 값을 가지는지 유추하기 쉽지 않다. 복소 지수 때문인데, 이 복소 지수 식을 사인 함수 식으로 바꿔보자. 오일러 공식을 쓰면 되겠다.

$$ e^{i\theta} = \cos {\theta} + i\sin {\theta} \\ e^{-i\theta} = \cos {\theta} – i\sin {\theta} \tag {오일러 공식}$$

식 (2)에서 $\theta =\pi f\Delta t$로 놓고 다시 쓰면,

$$ \begin {align} Y(f) &= \dfrac {1}{i2\pi f}(e^{i\theta} – e^{-i\theta}) \\ &= \dfrac {1}{i2\pi f}(\cos \theta + i\sin \theta -(\cos \theta – i\sin \theta) )\\ &= \dfrac {1}{i2\pi f}(2i\sin \theta) \\ &= \dfrac {1}{\pi f} \sin \theta = \dfrac {\sin {(\pi f \Delta t})}{\pi f} \end{align} \tag {3}$$

사인 함수로 바꿔보니 식 (3)과 같이 나왔다. 근데, 이 식도 바로 이용할 수는 없겠다. 왜냐면, $f=0$일 때의 값을 구해야는데(우리가 처음에 미리 예측하길 $f=0$에서 값이 있을 것이라고 예상했었다.), 식 (3)에서 $f$의 위치가 분모에 있어서 $f=0$으로 넣으면 분모가 $0$이 되어 계산할 수가 없다. (0으로 나누는 것은 불능이기에)

어떻게 할까?

삼각함수의 극한에서, 아래와 같은 성질이 있다.

$$ \lim _{x \rightarrow 0} {\dfrac {\sin x}{x}} = 1 \tag {삼각함수의 극한 정리}$$

위와 같이 되는 것은 분모와 분자에 대해 각각 미분을 해보면 쉽게 증명이 된다.

$$\begin {align} \lim _{x \rightarrow 0} {\frac {\sin x}{x}} & = \lim _{x \rightarrow 0} {\dfrac {\frac{\mathrm{d} }{\mathrm{d} x}\sin x}{\frac{\mathrm{d} }{\mathrm{d} x}x}} \\ &= \lim _{x \rightarrow 0} \frac {\cos x} {1} \\ &= \frac {1} {1} = 1 \end{align} $$

식 (3)을 삼각함수의 극한 성질을 이용할 수 있는 형태로 바꿔보자. $\dfrac {\Delta t}{\Delta t}$를 곱해주면 되겠다.

$$\begin {align} Y(f) &= \dfrac {\sin {(\pi f \Delta t})}{\pi f} \\ &= \dfrac {\sin {(\pi f \Delta t})\cdot \Delta t}{\pi f \Delta t} \end{align} \tag {4}$$

식 (4)에서 $\pi f\Delta t \rightarrow 0$으로 보내면 $\dfrac {\sin {\pi f\Delta t}}{\pi f\Delta t}=1$이 되겠다. 근데, 이 식에서 변수는 $f$이기에, $f$에 대해서만 생각하면, $\pi f\Delta t \rightarrow 0$은 $f \rightarrow 0$과 똑같다. 따라서, $f \rightarrow 0$으로 보내는 것으로 해서 식 (4)를 전개하면,

$$ \begin {align} \lim _{f \rightarrow 0} Y(f) &= \lim _{f \rightarrow 0} \dfrac {\sin {(\pi f \Delta t})\cdot \Delta t}{\pi f \Delta t} \\ &= 1 \cdot \Delta t \\ & = \Delta t \end{align} \tag {5}$$

드디어 값이 나왔다.

푸리에 변환을 해봤더니, $f\rightarrow 0$일 때 $Y(f)=\Delta t$가 되었다.

여기서 $\Delta t$는 적분을 하는 구간 범위였다. 즉, $Y(f)$의 값은 적분을 하는 구간인 $\Delta t$가 되고, 적분을 하는 구간을 크게하면 할수록 $Y(f)$의 값이 커지는 것이다.

$\Delta t$의 값을 조금씩 변경시키면서 그래프를 그려보자. 식 (4)를 이용하겠다.

(그림 5) $\Delta t=1$

(그림 6) $\Delta t=3$

(그림 7) $\Delta t = 5$

$\Delta t$의 값이 $1$일 때는 주파수가 0인 부분에서 좀 크긴하지만, 주파수가 0인 부분에서만 값이 존재할 것이라는 우리의 기대와는 다른 값이다. (우리는 처음부터 주파수가 0인 지점에서만 값이 존재할 것이라고 예상했었다.)

그러나 $\Delta t$의 값을 증가시켜가면, 점점 더 주파수가 0인 지점에서의 값이 커지고 있다.

$\Delta t$를 점점 더 증가시켜서 아주 큰 값이 되게해보자.

(그림 8) $\Delta t$가 증가할 때의 그래프 애니메이션

$\Delta t$가 아주 커지게 되면 주파수가 0인 부분에만 값이 남게 되겠다.

의미를 생각해보자.

먼저 $\Delta t=1$인 경우를 보면, 시간 간격을 매우 좁게 본 것이다. 원래는 무한대의 시간에 대해 계산을 해야 하는데, 아주 좁은 시간 영역만 보고, 그에 대한 주파수 성분을 유추해본 셈이다. 따라서, 무한대의 시간 간격을 가지고 봤을 때는 주파수가 0인 부분에만 값이 존재하겠지만, 적은 시간 간격의 정보만을 가지고 가지고 유추해보면 다른 주파수 성분도 있다는 오차가 발생하는 것이다.

여기서 주파수가 0인 부분 파형의 산의 너비를 $\Delta f$로 놓으면,

$\Delta t$의 값이 커질수록 $\Delta f$의 값이 작아지고, $\Delta t \rightarrow \infty$일 때는 $\Delta f \rightarrow 0$이 된다. 반대로 $\Delta t \rightarrow 0$이면 $\Delta f \rightarrow \infty$가 될 것이다.

$\Delta t \rightarrow \infty$ 이면 $\Delta f \rightarrow 0$

$\Delta t \rightarrow 0$ 이면 $\Delta f \rightarrow \infty$

이 처럼 $\Delta t$를 0으로 보내도, $\Delta f$를 0으로 보내도 두 값의 곱은 절대 0이 되지 않는다.

$$ \Delta t \times \Delta f \geq C \; , where \; C > 0 \tag {6}$$

식 (6)은 “입자의 위치와 운동량에 대한 정확한 값을 동시에 알 수 없다”는 ‘불확정성의 원리’와 닮아 있다.

(그림 4)에서 파동의 정확한 위치를 지정하기 위해 $\Delta t$를 줄이면, (그림 5)에서와 같이 정확한 주파수의 세기를 알 수 없었다.

푸리에 변환에 대해서 다시 생각해보자.

푸리에 변환은, 시간에 따라 ‘위치’가 변하는 파동 함수를, ‘운동량(세기)’이 다른 정현파의 합으로 표현하는 것이다.

여기서 정확한 ‘위치’를 한정하면 정확한 ‘운동량’을 알 수 없다.

즉, 푸리에 변환에서도 ‘불확정성의 원리’가 존재한다.

-끝-

반응형

푸리에 변환에 대한 정확한 분석(Fourier Transform)

반응형

푸리에 급수 다음 등장하는 푸리에 변환은 적분변환(Integral Transform) 의 알파이자 오메가입니다. 대학에서 수학을 사용하는 학과에서 배우지 않을 수 없는 개념이고, 활용도는 무궁무진합니다. 변환이라는 특성상 단순 수학적 기법에서의 변환 의미를 넘어, 일상 생활에서 파동에 관한 장치들에 빠지지 않고 응용되기에 푸리에 변환은 오히려 수학과보다 공대생들에게 자주 쓰이는 도구일지도 모릅니다. 그러나 대부분의 학생은 여기까지의 말을 ‘들어만’ 봤지 ‘이해하지는’ 못하고 웹서핑과 유튜브의 무한 반복에 지쳐 쓰러집니다.

실제로 푸리에 변환의 수학적 의미가 아니라 활용적 의미, 과학적 의미는 수많은 유튜브 영상에서 그림과 함께 보여주고 있습니다. 실험이나 그래프 시뮬레이션 프로그램을 통해서 푸리에 변환을 직접적으로 보며 경험할 수 있고 일상 생활의 어떤 장치에서 활용되는지도 알려주는 좋은 동영상들이 많습니다. 예컨대 2019학년도 수능까지 물리1에서는 고주파/저주파 필터(High pass/Low pass)에 관해 배웠었는데, 이는 회로에서 주파수를 걸러 보낼 수도 있고, 보내지 않을 수도 있는 과학적 원리가 숨어져 있지만 그 밑바닥엔 주파수를 푸리에 변환을 통해 걸러 내는 수학적 원리가 숨겨져 있습니다.

하지만, 다시 연필을 잡고 수학을 공부하는 자리로 돌아와봅시다. 어떤 수학적 개념을 익히고 이해할 때 우리는 그것이 실생활에서 어떻게 활용되는지를 안다고 해결되지 않으며, 냉정히 말하면 수학적인 방법부터 체득해야 적용의 원리로 나아갈 수 있는 것입니다. 푸리에 변환이 무엇인지 ‘수학적으로’ 답하고 이해해야 그것의 활용까지 바라볼 수 있을 거라는 뜻입니다. 그러므로 이 블로그는 언제나 그랬듯이 직접 연필을 들고 종이와 함께 푸리에 해석을 뚫어나갈 수 있는 힘을 길러주기 위해, 그것의 수학적 이해에 초점을 맞추어 설명할 것입니다. 그리고 저는 아무래도 순수 과학을 공부하는 입장이기에 공학적 활용이 궁금하신 분들은 좋은 영상들을 참고하는 것이 유리할 수 있을 것 같습니다.

참고로 물리학에서도 푸리에 변환은 양자역학에서 쓸모가 많습니다. 슈뢰딩거 방정식에 등장하는 파동함수의 모양 자체부터 푸리에 해석으로 건설되어 있습니다. 그 까닭은 양자역학이 물질의 파동성을 설명하는 분야이기 때문입니다.

1. 푸리에 변환(Forier Transfomation)

1) 정의

중요한 식인 만큼 정의를 먼저 하고 가겠습니다.

함수 $f(x)$ 에 대한 푸리에 변환식은 다음과 같다. ($f$는 주기함수가 아니어도 된다.)

$$f(x)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}g(\omega)e^{\displaystyle i\omega x}\,d\omega$$ $$g(\omega)=\frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty}f(x)e^{\displaystyle -i\omega x}\,dx$$

여기서 두 식의 우변 가장 앞에 붙은 계수를 각각 $A,B$라 하면, $AB=\displaystyle\frac{1}{2\pi}$ 가 되도록 나누어 붙일 수 있다. 위와 같이 각각 $\displaystyle\frac{1}{\sqrt{2\pi}}$ 을 취하는 것이 보편적이다.

$f$ 와 $g$ 의 관계를 유심히 살펴보시기 바랍니다. $f=f(x)$ 이고 $g=g(\omega)$ 인 함수입니다. 그래서 $f$ 는 $g$ 를 $\omega$ 에 대해 적분해야 하고, $g$ 는 $f$ 를 $x$ 에 대해 적분한 모습입니다.

그리고 $g$ 에서 $\omega$ 라는 문자를 사용했는데, 이는 물리학에서 푸리에 변환을 할 때 식에 들어있는 $\omega$ 가 ‘각진동수(angular frequency)’를 의미하기 때문입니다. 순수 수학에서 푸리에 변환식을 작성할 땐 그러니 굳이 $\omega$ 를 사용해야 하는 것은 아니며 $t$로 놓는 것이 보편적인 표기법입니다.

2. 푸리에 해석의 탄생 과정? 관점?

1) 시그마는 적분으로, 급수는 변환으로?

푸리에 변환은 크게 두 가지 관점으로 볼 수 있다고 설명할 것입니다. 첫번째의 것은 급수를 정적분으로 바꾸는 관점입니다. 푸리에 급수의 지수함수 형태

$$f(x)=\sum_{n=-\infty}^{\infty}c_ne^{\displaystyle \frac{in\pi x}{l}}\\\\

c_n=\frac{1}{2l}\int_{-l}^{l}f(x)e^{\displaystyle \frac{in\pi x}{l}}dx$$

에 대하여 시그마가 달려 있고 무한개의 항이 존재하니 이를 리만합으로 고려해서 정적분으로 바꿔보는 시도가 가능하다는 뜻입니다. 급수를 정적분으로 바꾸기 위해 다음과 같은 작업을 진행합니다.

$$c_n\;\;\rightarrow \;\; g(\alpha) \\\\\\

n\;\; \rightarrow \;\; \alpha \\\\\\

\sum_{-\infty}^{\infty} \;\;\rightarrow \;\; \int_{-\infty}^{\infty} \\\\$$그런 다음 한 조각에 대한 정의는

$$\alpha_n=\frac{n\pi}{l}\;\;,\;\;\Delta \alpha = \alpha_{n+1}-\alpha_n=\frac{\pi}{l}$$

으로 정하면, 주어진 계수 $c_n$ 은

$$c_n=\frac{\Delta \alpha}{2\pi}\int_{-l}^{l}f(x)e^{\displaystyle -\frac{in\pi x}{l}}dx =

\frac{\Delta \alpha}{2\pi}\int_{-l}^{l}f(u)e^{\displaystyle -\frac{i\alpha_n u}{l}}du$$

이 됩니다. 여기서 혼동을 피하기 위해서 $x$대신 $u$를 사용했습니다. 또한 쓰이고 있는 $\alpha $ 는 위 박스에서 $\omega$ 랑 같은 녀석입니다.

그러면 $f(x)$를 다음과 같이 정리합니다.

$$\begin{align*}

f(x)&=\sum_{n=-\infty}^{\infty}\left\{ \frac{\Delta \alpha}{2\pi}\int_{-l}^{l}f(u)e^{-i\alpha_n u}du \right\}\,e^{i\alpha_n x} \\\\&

=\sum_{n=-\infty}^{\infty}\frac{\Delta \alpha}{2\pi}\int_{-l}^{l}f(u)e^{i\alpha_n (x-u)}du \\\\&

=\frac{1}{2\pi}\sum_{n=-\infty}^{\infty} F(\alpha_n)\Delta\alpha \;\;\;\;\; \mathrm{where}\;\;\;\;\; F(\alpha_n)

=\int_{-l}^{l}f(u)^{i\alpha_n(x-u)}du

\end{align*}$$

이렇게 되면 $F(\alpha_n)$ 이라는 함수에 대한 리만합 형태가 만들어지고, 다시 $F(\alpha_n)$ 이라는 함수는 적분형태입니다. 곧 적분 안에 적분식이 들어있는 꼴이죠. 무한급수 형태 $\displaystyle\sum_{n=-\infty}^{\infty} F(\alpha_n)\Delta\alpha$ 은 $\Delta\alpha \;\;\rightarrow \;\; 0$ 로 보내는 극한에서 정적분이 될 수 있습니다. 그러려면 $l\;\;\rightarrow \;\;\infty$ 이면 되고, 그로 인해 $\Delta\alpha=\displaystyle\frac{\pi}{l}\;\;\rightarrow 0$ 에 가까워지게 됩니다. 따라서

$$\displaystyle \sum_{n=-\infty}^{\infty} F(\alpha_n)\Delta\alpha \;\; \to \;\; \displaystyle \int_{-\infty}^{\infty}

F(\alpha)d\alpha$$

가 됩니다. 이 때 원래 $\alpha_n$ 으로 달려 있던 첨자 $n$은 $\alpha$ 가 연속 변수가 되었기 때문에 삭제할 수 있습니다. 정리하면 $l\;\;\to\;\;\infty$ 이고 $\alpha_n=\alpha$ 가 되어

$$\begin{align*}

&F(\alpha)=\displaystyle \int_{-\infty}^{\infty} f(u)e^{i\alpha (x-u)}du \;\;\;\;\;\cdots \;\;\;\;\;(1)

\\\\&f(x)=\frac{1}{2\pi}\int_{-\infty}^{\infty}

F(\alpha)d\alpha

\end{align*}$$

가 되겠지요? 그럼 $(1)$을 $(2)$에 넣어 정리해주면 됩니다.

$$\begin{align*}

f(x)&=\frac{1}{2\pi}\int_{-\infty}^{\infty}

F(\alpha)d\alpha \\\\&=

\frac{1}{2\pi}\int_{-\infty}^{\infty}\displaystyle \int_{-\infty}^{\infty} f(u)e^{i\alpha (x-u)}\,du\,d\alpha

\\\\&= \frac{1}{2\pi}\int_{-\infty}^{\infty} e^{i\alpha x}\,d\alpha \int_{-\infty}^{\infty}

f(u)e^{-i\alpha u}\,du \\\\&=\int_{-\infty}^{\infty}

\left( \frac{1}{2\pi}\int_{-\infty}^{\infty}

f(u)e^{-i\alpha u}\,du \right)\,e^{i\alpha x}\,d\alpha \\\\&\equiv

\int_{-\infty}^{\infty} g(\alpha)e^{i\alpha x}\,d\alpha

\end{align*}$$

2) 내적의 의미를 상기해보자.

내적공간에서 정의된 벡터간의 연산 내적(Inner product)는 두 함수의 연관성을 측정하는 것임을 설명한 바 있습니다. 1이란 값은 방향이 정확히 일치하는 것이니 선형종속인 것이고, 0인 관계를 만족하면 직교(orthogonal)의 의미를 가지며 선형독립임은 물론 기저로서의 값어치도 훌륭합니다. 0도 1도 아닌 값을 가지면 선형독립인 관계는 맞지만 직교하진 않으니 (기저로 쓰기에는) 딱히 재밌지는 않을 것입니다.

아니, 뭔 링크가 이렇게 많냐고요? 이는 두번째 관점을 제대로 이해하려면 선형대수에 관한 선행지식이 많이 필요하다는 것을 뜻합니다. 그러니 위 내용들에 관한 이해를 마치기 전에는 바쁘면 단순히 첫번째 관점으로 푸리에 변환을 받아들이면 그만입니다. 그런데 사실 이 두번째 관점을 이해해야 공학에서 파동으로부터 주파수를 추출하는 수학적 원리를 파악할 수 있습니다.

푸리에 변환식을 보면 함수 $f(x)$는 $g=g(\omega)$ 와 $e^{\displaystyle i\alpha x}$ 의 곱이고 주어진 구간에 적분을 취한 상황입니다. 이는 함수 사이의 내적식과 똑같습니다. 이 내적이 의미하는 바가 무엇일까요? 우선 오일러 공식에 의하면,

$$e^{i\omega x}=\cos \omega x+i\sin \omega x$$

의 관계는 다들 아실 겁니다. 그러면 지수에 허수단위 $i$를 품은 지수함수 $e^{i\omega x}$ 는 거대한 의미를 갖습니다. 왜냐하면 이 함수는 복소평면에서 실수성분이 $\cos \omega x$ 인 것이고 허수부분이 $\sin \omega x$ 라는 뜻이니, 이 둘을 직교기저(orthogonal basis)로 택해 복소평면상의 임의의 복소수를 나타낼 수 있는 선형결합 표현이기 때문입니다!!

이 내용은 수학적으로 어마어마한 무게가 있습니다. $\sin$ 과 $\cos$ 이 직교기저를 이룬다는건, 두 기저 자체가 파동을 표현하는 아주 단순한 형태기 때문에, 이들의 선형결합을 통해서 임의의 파동을 나타낼 수 있다는 것입니다. 이미 푸리에 급수는 이 모든 것들까지는 함의하고 있습니다. 그렇다면 나아가서 적분식인 푸리에 변환은 내적을 의미하는 것이니, 다른 함수 $g(\omega)$ 를 가져와 우리의 지수함수 $e^{i\omega x}$ 와 비교질을 하겠다는 것이죠. 그러면 내적의 결과이니 0부터 1까지의 관련성을 보여줄 것입니다.

조금더 구체적으로 설명해 볼까요? 만일 내가 푸리에 변환식에 어떤 파형 $g(\omega)$ 를 가져오면, 여기다 우리의 측정 기준 $e^{i\omega x}$ 를 곱해서 적분했을 때, 값이 나올 것입니다. 그 값은 측정기준 $e^{i\omega x}$ 와 $g(\omega)$ 가 관련성이 높을수록 0보다 큰 높은 값을 토해냅니다. 이 때 $g$ 가 여러가지 주파수가 혼합되어있는 파동일 때, 즉 사인형 파동도 있고 코사인형 파동도 있다고 해도, $e^{i\omega x}$ 는 사인과 코사인이라는 두 기저를 전부 가지고 있으니 사인파끼리, 코사인파끼리 연관성을 모두 다 측정할 수 있으며, 기가 막히게 코사인끼리의 값은 $\mathbf{Re}$ 파트로, 사인끼리의 값은 $\mathrm{Im}$ 파트로 모입니다. 오일러 공식 때문이지요.

공학적으로 설명하면 이는 $g$ 라는 불규칙해 보이는 파형을 하나 가져 와서 그대로 두고, 측정 기능을 가진 $e^{i\omega x}$ 와 내적을 시키는데, 이 과정에서 $e^{i\omega x}$ 의 $\omega$ 를 조금씩 바꾸면 특정 주파수를 추출할 수 있습니다. 아직도 감이 안 잡힐 수 있으니 예시를 들어 봅시다. 예컨대 $g$ 가 간단히 각진동수 $\omega=5$ 인 사인파와 $\omega =3$ 인 코사인파의 선형결합으로 이루어진 파형이라고 해봅시다.

$$g(\omega)=A\cos(2\pi\cdot3 \cdot t)+B\sin\left( 2\pi\cdot5 \cdot t \right)$$

여기서 만일 측정 기준 지수함수를 $e^{-i\omega x}=e^{-3i x}$ 으로 택하는 경우, $e^{-i\omega x}=e^{-3i x}$ 의 코사인 부분 $\cos 3x$ 가 $A\cos(2\pi\cdot3 \cdot t)$ 와 걸려 0이 아닌 값을 내놓습니다. 그리고 이 때 그 수치는 진폭 $A$에 비례합니다. 반면 지수함수의 사인부분 $\sin 3x$ 는 $g$와 주파수가 다르기 때문에 내적해도 값이 0입니다. 이유는 삼각함수들의 내적관계 때문이겠죠?

반대로 지수함수를 $e^{-i\omega x}=e^{-5i x}$ 로 택하는 경우 위와 같은 원리로 코사인 파트는 주파수가 다르니 0이 되고, 사인부분만 주파수가 같으니 $B$에 비례하는 값이 나옵니다.
[그림 1] ‘영상의 초반부에 $f$ 가 푸리에 급수로 분해되어 파란색으로 표시된다. 이 사인파들을 주파수에 따라 나열하면 영상의 후반부에 나타나는 것처럼&nbsp; 디랙 델타 함수의 꼴로 표시된다. 이 때 주파수 영역에서의 함수를 $\hat{f}$ 로 표시한다.’ 라고 위키백과에서 설명하고 있다.

실제 파동에 대한 푸리에 변환은 이 지수함수 $e^{-i\omega x}$ 의 각진동수 $\omega$ 에 수많은 값을 넣어서 수많은 적분을 수행합니다. 그러면 주파수(독립변수)에 따른 내적값($A,B$ 에 비례, 종속변수)를 그래프로 나타낼 수 있어서, 이 주파수-결과값 그래프를 좌표평면에 그리면 정확히 주파수가 3인 곳과 5인 곳에 나타납니다. 즉 3과 5일 때만 값이 치솟고 그 주변은 0에 수렴하기 때문에, 위 [그림 1]에서 이것의 그래프가 ‘디랙 델타 함수(Dirac delta function)’ 꼴로 그려진다는 뜻이며, 이를 $\hat{f}$ 이라 표시하고 있습니다. 물론, 앞서 설명했듯이 3은 코사인에서 온 것이니 실수부분, 5는 허수부분으로 취급해서 표현하게 되고요. 이것이 바로 공학에서 주파수 필터를 만들 수 있는, 수학적 기반이자 원리입니다.

제 블로그는 되도록이면 글로 서술하는 것을 선호하는데 사실 푸리에 변환만큼은 영상으로 보는 것이 좋습니다. 다만 그러한 영상을 ‘보는’ 것만으로 ‘이해’의 영역에 접근하기는 곤란할 것이고, 감을 잡는다 해도 그 감은 금방 휘발됩니다. 글로 서술된 수학적 원리를 절실히 타파하여 본인의 것으로 만들기를 권합니다.

반응형

다크 프로그래머 :: Fourier Transform(푸리에 변환)의 이해와 활용

푸리에 변환(Fourier transform)에 대해서는 예전부터 한번 정리를 해야겠다고 생각만 했었는데 이번에 기회가 되어 글을 올립니다.

푸리에 변환(Fourier transform)은 신호처리, 음성, 통신 분야에서 뿐만 아니라 영상처리에서도 매우 중요한 개념으로 다양한 응용을 가지고 있습니다. 영상을 주파수 성분으로 변환하여 다양한 분석 및 처리를 할 수 있고 임의의 필터링 연산을 fft(fast Fourier transform)를 이용하여 고속으로 구현할 수도 있습니다. 그리고 푸리에 변환과 같은 근원적인 이론들은 특정 응용에 국한되지 않기 때문에 한번 알아두면 분야를 떠나서 두고두고 도움이 됩니다.

이 글에서는 푸리에 변환(Fourier transform)이 무엇이고 어디에 쓸 수 있는지, 그리고 어떻게 쓸 수 있는지 직관적 이해와 유용한 성질들, 영상처리 응용, 그리고 푸리에 변환(Fourier transform)을 실제 활용하는데 있어서 필요한 사항들을 최대한 직관적으로 정리하고자 합니다.

그동안 푸리에 변환(Fourier transform)에 대해 개인적으로 가지고 있었던 의문은 푸리에 변환을 통해 얻어지는 스펙트럼과 페이즈(phase) 중 페이즈(phase)가 무엇인가? 그리고 푸리에 주파수 공간의 좌표값을 어떻게 해석할까입니다. 아마도 비슷한 의문을 가진 분들도 꽤 있을 것으로 생각됩니다. 이 글을 통해서 그러한 의문에 대한 답도 같이 다루게 됩니다.

1. 푸리에 변환(Fourier transform) – 직관적 이해

모든 공부의 시작은 핵심 개념을 정확히 이해하는데 있다. 그리고 그 이해는 가급적 직관적일수록 좋다.

푸리에 변환(Fourier transform)을 직관적으로 설명하면 푸리에 변환은 임의의 입력 신호를 다양한 주파수를 갖는 주기함수들의 합으로 분해하여 표현하는 것이다.

좀더 들어가면, 푸리에 변환에서 사용하는 주기함수는 sin, cos 삼각함수이며 푸리에 변환은 고주파부터 저주파까지 다양한 주파수 대역의 sin, cos 함수들로 원본 신호를 분해하는 것이다.

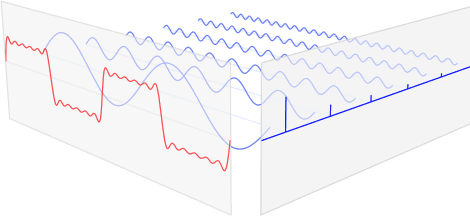
아래 그림(그림 1)의 예를 보자. 맨 앞의 붉은 색 신호는 입력 신호이고 뒤의 파란색 신호들은 푸리에 변환(Fourier transform)을 통해 얻어진 (원본 신호를 구성하는) 주기함수 성분들이다. 각각의 주기함수 성분들은 고유의 주파수(frequency)와 강도(amplitude)를 가지고 있으며 이들을 모두 합치면 원본 붉은색 신호가 된다.

그림 1. 푸리에 변환 (그림출처: 위키피디아)

여기서 입력 신호는 전파, 음성 신호 등과 같이 시간축(time)에 대해 정의된 신호일 수도 있고 이미지(image) 등과 같이 공간축에 대해 정의된 신호일 수도 있다. 통신 분야에서는 푸리에 변환(Fourier transform)을 time domain에서 frequency domain으로의 변환이라고 하고, 컴퓨터 비전(computer vision), 영상처리 쪽에서는 spatial domain에서 frequency domain으로의 변환이라고 부른다. 명칭이야 어쨌든 그 핵심은 입력 신호를 sin, cos의 주기성분으로 분해하는 것이다.

푸리에 변환(Fourier transform)의 대단한 점은 입력 신호가 어떤 신호이든지 관계없이 임의의 입력 신호를 sin, cos 주기함수들의 합으로 항상 분해할 수 있다는 것이다. 그리고 그 과정을 수식으로 표현한 것이 푸리에 변환식이다.

2. 푸리에 변환(Fourier transform) – 수식적 이해

어떤 개념을 직관적으로 이해했다면 그 개념에 대한 수식적 이해는 그 개념을 한층 풍성하고 깊이있게 이해하게 해 준다.

푸리에 변환(Fourier transform)은 프랑스의 수학자 Joseph Fourier (1768 ~ 1830)가 제안한 방법으로서 수학사(해석학)의 역사가 새로 씌여질 정도로 대단한 발견이었다고 한다. 그 유명한 푸리에 변환의 수식은 다음과 같다.

, — (1)

. — (2)

여기서 j는 허수단위 , f(x)는 원본 입력 신호, ej2πux는 주파수 u인 주기함수 성분, F(u)는 해당 주기함수 성분의 계수(coefficient)를 나타낸다.

일단 식을 있는 그대로 해석하면 식 (1)은 입력신호 f(x)가 ej2πux들의 합으로 표현(분해)된다는 의미이다 (적분은 합한다는 의미를 갖는다). 그리고 식 (2)는 f(x)를 주기함수 성분으로 분해했을 때의 계수(coefficient) F(u)가 식 (2)로 주어진다는 의미이다. 앞서 그림 1과 연관해 보면 ej2πux는 f(x)를 구성하는 (파란색의 주파수 u인) 주기함수 성분들이고 F(u)는 해당 주기함수 성분의 강도(amplitude)를 나타낸다.

☞ 푸리에 변환에 대한 일반적인 설명 방식은 두번째 식 (2)를 푸리에 변환이라고 정의하고 첫번째 식 (1)을 푸리에 역변환(inverse Fourier transform)이라고 정의하는 것이다. 그리고 푸리에 역변환을 하면 다시 원래의 함수로 돌아온다고 한다. 하지만 이러한 기계적인 이해(푸리에 변환을 어디 하늘에서 뚝 떨어진 정의로만 받아들이는 것)는 푸리에 변환의 본질을 이해하는데 별 도움이 되지 않는다.

이제 식으로 좀더 들어가 보자. 일단, 식 자체는 푸리에 변환의 대단함에 비추어 매우 단순하다 (Simple is the best!!). 다만 한 가지 ej2πux의 의미만 이해하면 된다. 그리고 이를 위해서는 오일러 공식(Euler’s formula)이 필요하다.

오일러 공식(Euler’s formula)은 복소지수함수를 삼각함수로 변환할 수 있도록 하는 유명한 식이다.

— (3)

식 (3)은 증명 가능한 식이며 그 증명은 인터넷에서 어렵지 않게 찾을 수 있다. 어쨌든 오일러 공식을 이용하면 식 (1)의 ej2πux는 실수부가 cos(2πux), 허수부가 sin(2πux)인 주기함수임을 알 수 있다.

— (4)

여기서 cos(2πux), sin(2πux) 모두 주기(period)가 1/u, 주파수(frequency) u인 주기함수이므로 결국 ej2πux는 주파수 u인 정현파(sinusoidal wave)의 복소지수함수 표현임을 알 수 있다.

주기: 파동이 한번 진동하는데 걸리는 시간, 또는 그 길이. sin(wx)의 주기는 2π/w 임.

주파수: 1초 동안의 진동 횟수. 주파수와 주기는 서로 역수 관계 (주파수 = 1/주기)

☞ 정현파(sinusoidal wave)는 파형이 sin 또는 cos 함수인 파동(wave)을 말한다. 그런데, 여기서 왜 갑자기 복소수가 나오고 또 주기함수를 저렇게 표현하느냐고 따질 수 있다. 하지만 여기서는 그냥 복수지수함수는 정현파(sinusoidal wave)를 표현하는 방법 중 하나라는 정도로만 알아두자. 정현파 및 복수지수함수 표현에 대한 보다 자세한 내용은 AngeloYeo님의 페이저(phasor)에 대한 설명글을 참고하기 바란다.

이제 다시 원래의 식 (1), (2)로 돌아가 보자. 식 (1)은 함수 f(x)를 모든 가능한 주파수(u)의 주기함수들(ej2πux)의 일차결합으로 표현한 것이다. 그리고 그 일차결합 계수 F(u)는 식 (2)로 항상 주어질 수 있다는 것이 요지이다. 이와 같이 푸리에 변환식을 볼 수 있다면 푸리에 변환의 핵심을 이해한 것이다.

☞ 식 (1), (2)의 푸리에 변환(Fourier transform)식은 언뜻 보면 정의(definition)로 보이지만 사실은 증명해야 할 정리(theorem)이다. 즉, 식 (2)의 F(u)를 식 (1)에 대입하면 항상 f(x)가 나옴을 증명해야 한다. 이것이 증명되면 모든 임의의 신호함수는 항상 주기함수들의 일차결합으로 분해될 수 있음이 증명되는 것이다 (증명은 이곳 참조).

마지막으로, (증명은 아니지만) 왜 일차결합의 계수 F(u)가 식 (2)로 주어지는지를 선형대수학과 연관지어 직관적으로 이해해 보자. 식 (1)에서 ej2πux, u = 0, ±1, ±2, …은 모든 신호를 생성할 수 있는 직교(orthogonal) 기저(basis) 함수들로 볼 수 있다 (편의상 u를 정수 범위로 표기했으나 u는 실수 전체 범위임). 그러면 입력 신호 f(x)를 이들 기저함수들로 분해했을 때의 계수 F(u)는 f(x)와 기저함수의 내적(dot product)으로 계산될 수 있다 (아래의 ☞선형대수학 관련 설명 참조). 식 (2)는 f(x)와 ej2πux의 함수 내적이기 때문에 그 결과는 f(x)를 ej2πux들로 분해했을 때의 계수가 된다. 따라서, F(u)가 식 (2)로 주어지는 이유가 설명이 되었다. 참고로, 식 (2)에서 j 앞에 -가 붙은 이유는 복소수에서의 내적은 어느 한쪽에 켤레(conjugate) 복소수를 취한 후 계산되기 때문이다.

☞ 선형대수학(linear algebra)에서는 어떤 벡터 공간을 생성할 수 있는 일차독립인 벡터들의 집합을 기저(basis)라고 한다. 만일 기저(basis) 벡터들이 v1, v2, …, vn라 하면 이 벡터공간에 속하는 임의의 벡터 v는 v = a1v1 + a2v2 + … + anvn (ai는 상수)와 같이 기저 벡터들의 일차결합으로 표현될 수 있다 (왜냐하면 vi들이 이 벡터공간의 모든 벡터들을 생성할 수 있으니까). 그런데 만일 기저벡터들이 서로 수직(vi·vj = 0)인 단위벡터라면 일차결합 계수 ai는 내적을 이용하여 ai = v·vi로 손쉽게 계산할 수 있다 (∵ v·vi = (a1v1 + … + anvn)·vi = ai*(vi·vi) = ai). 어떤 벡터와 기저(basis) 벡터를 내적하면 이 벡터에 포함된 기저 성분의 계수가 얻어진다는 것은 선형대수학에서 매우 유용한 성질이다.

☞ F(u)가 식 (2)로 주어지는 이유에 대한 선형대수학적 설명은 개인적 이해 방식이라서 증명이 있거나 근거 문헌이 있는 내용은 아닙니다. 그냥 그런 식으로 이해할 수도 있구나 하고 참고만 하기 바랍니다. 정말 그런지 수학적으로 증명해 봐라 하면 골치아픕니다..

3. 이미지(영상신호)에서의 푸리에 변환(Fourier transform)

푸리에 변환(Fourier transform)을 영상처리에 적용하기 위해서는 이미지(영상신호)가 가지고 있는 몇 가지 차이점을 인지해야 한다. 먼저, 이미지는 2차원의(x축 방향의 변화와 y축 방향의 변화가 동시에 포함된) 신호이기 때문에 2차원에서 정의되는 푸리에 변환이 필요하다. 2차원 신호에 대한 푸리에 변환(Fourier transform)은 다음과 같이 정의된다.

, — (5)

. — (6)

단, 여기서 F(u, v)는 x축 방향으로 주파수(frequency) u, y축 방향으로 v인 주기함수 성분의 계수이다. 그리고 그 값은 식 (6)에 의해 계산된다.

그런데 이미지는 연속(continuous)이 아닌 이산(discrete) 신호이다. 그리고 한정된 유한(finite) 구간에서 정의되는 신호이다. 따라서, 이산 데이터에서 정의되는 푸리에 변환이 필요하다. W x H 크기의 이미지 f(x, y)에 대한 이산 푸리에 변환(discrete Fourier transform)은 다음과 같이 정의된다.

, —(7)

. —(8)

단, x = 0, 1, …, W-1, y = 0, 1, …, H-1이고 u = 0, 1, …, W-1, v = 0, 1, …, H-1.

식 (7)에서 ej2π(ux/W+vy/H)는 x축 방향으로 주파수가 u/W, y축 방향으로 주파수가 v/H인 sinusoidal 주기함수이다 (by 오일러 공식). 일반적인 푸리에 변환식과는 달리 W와 H로의 나누기가 들어있음에 유의해야 하며 이는 데이터가 정의된 구간을 하나의 단위 주기(unit period)로 만드는 효과가 있다. 일종의 정규화 팩터(normalization factor)라고 생각하면 된다.

여기서 2D 이미지를 어떻게 신호로 해석할 수 있는지, 그리고 2D 정현파(sinusoidal wave) ej2π(ux/W+vy/H)가 도대체 어떤 모습일지 아마도 의아해할 수 있다. 첫째, 이미지를 신호로 해석하는 문제는 x 또는 y축을 시간축으로 놓고 좌표의 변화에 따라 변하는 이미지 픽셀의 밝기 변화를 신호로 생각하면 쉽게 이해할 수 있다. 다음으로, 2D에서 정의되는 정현파(sinusoidal wave)의 모습은 아래 그림과 같이 모든 방향으로의 단면이 sinusoidal이 되는 물결 형태의 파동을 생각하면 된다.

그림 2. 2D에서의 sinusoidal wave

앞서 그림 1의 1D 푸리에 변환의 경우와 유사하게 생각해 보면, 이미지에 대한 푸리에 변환(Fourier transform)은 그림 2와 같은 형태의 다양한 2D 정현파들의 합으로 이미지를 분해하여 표현하는 것으로 이해할 수 있다.

이미지에 대한 푸리에 변환(Fourier transform)에서 한 가지 주의해야 할 것은 푸리에 변환의 계수 F(u, v)가 ej2π(ux+vy)의 계수가 아니라 ej2π(ux/W+vy/H)의 계수라는 점이다. 즉, 이산 푸리에 변환에서 F(u, v)는 주파수 u, v 성분이 아니라 주파수 u/W, v/H 성분에 대한 계수를 나타낸다.

W × H 이미지에 대한 이산 푸리에 변환에서 F(u, v)는 – x축 주파수 u/W, y축 주파수 v/H인 주기함수 성분에 대응 – 주기로는 x축 방향 W/u 픽셀, y축 방향 H/v 픽셀인 주기성분을 나타냄 (주기 = 1/주파수)

☞ 바로 이 부분이 개인적으로 푸리에 변환에 대해서 혼동스러웠던 부분 중 하나이다. W x H 이미지의 푸리에 변환에서 F(u, v)는 주파수 u, v의 성분이 아니라 주파수 u/W, v/H 성분이다. 따라서, 주파수 공간에서 특정 F(u, v) 값이 높게 나타났다면 원래의 이미지 공간에서는 x축 방향으로 주기가 W/u 픽셀, y축 방향 주기가 H/v 픽셀인 주기성 성분이 존재한다는 의미가 된다.

참고로, 1차원에서의 함수 f(x), x = 0, 1, 2, …, W-1에 대한 이산 푸리에 변환(discrete Fourier transform)은 다음과 같이 정의된다.

— (9)

— (10)

☞ 1차원 이산 푸리에 변환(discrete Fourier transform)식은 실제 푸리에 변환을 컴퓨터로 구현하는데 있어서 가장 기본이 되는 식이다. 왜냐하면 파동과 같은 연속 신호라 할지라도 실제 분석에 있어서는 샘플링된 이산 데이터를 이용해야 하고 2차원 푸리에 변환에 대한 구현도 내부적으로는 1차원 푸리에 변환을 이용하여 구현되기 때문이다.

4. 푸리에 스펙트럼(spectrum)과 페이즈(phase)

이제 실제로 푸리에 변환(Fourier transform)을 통해 얻어지는 F(u, v) 값들이 어떤 의미를 가지며 어떤 형태(visualization)를 갖는지 살펴보자.

푸리에 변환을 통해 얻어지는 F(u, v)는 복소수(complex number)이며 실수부(Real)와 허수부(Imaginary)로 구성된다 (1차원 푸리에 변환의 경우도 마찬가지이다).

— (11)

이 때, 복소수 F(u, v)의 크기 |F(u, v)|를 푸리에 변환의 spectrum(스펙트럼) 또는 magnitude라고 부르고, F(u, v)의 각도 Φ를 phase(페이즈) angle 또는 phase spectrum이라고 부른다.

— (12)

— (13)

A. 푸리에 스펙트럼(Fourier spectrum)

먼저, 푸리에 스펙트럼(Fourier spectrum)에 대해 살펴보자. 푸리에 스펙트럼은 해당 주파수 성분이 원 신호(이미지)에 얼마나 강하게 포함되어 있는지를 나타낸다. W x H 이미지를 푸리에 변환(Fourier transform)하면 식 (7), (8)에 의해 W x H의 F(u, v), u = 0, …, W-1, v = 0, …, H-1 가 얻어진다. 따라서, |F(u, v)|를 픽셀값으로 잡으면 아래 예와 같이 푸리에 스펙트럼을 원본 이미지와 동일한 크기의 이미지로 시각화할 수 있다.

그림 3. 푸리에 스펙트럼(spectrum)과 좌표계

(a) 입력 이미지, (b) 푸리에 스펙트럼, (c) shifted 스펙트럼

푸리에 스펙트럼(Fourier spectrum)을 이미지로 시각화하는 데에는 2가지 문제점이 있다. 먼저, 푸리에 스펙트럼은 저주파 영역은 매우 큰 값을 갖는 반면에 대부분의 다른 영역은 0에 가까운 값을 갖는다. 따라서 푸리에 스펙트럼을 그대로 이미지로 시각화하면 검은 바탕 위에 흰점 하나만 존재하는 형태가 된다. 이러한 문제를 해결하기 위해서 스펙트럼을 이미지로 표현할 때에는 그림 3(b)처럼 스펙트럼에 log를 취하는 것이 일반적이다. 다음으로, 원래의 스펙트럼 이미지는 그림 3(b)처럼 모서리로 갈수록 값이 높아지기 때문에 스펙트럼의 형태를 파악하기 힘들다. 따라서 이러한 문제를 해결하기 위해 그림 3(c)처럼 원점이 중심(center)에 오도록 스펙트럼의 위치를 이동시킨(shift) 형태의 이미지를 사용하는 것이 일반적이다 (아래 ☞설명 참조). 앞으로 푸리에 스펙트럼 이미지라 하면 그림 3(c)와 같은 shifted 스펙트럼 이미지를 생각하면 된다.

☞ 그림 3(c)와 같은 shift가 가능한 이유는 푸리에 스펙트럼이 원점대칭인 주기함수이기 때문이다. 사실 식 (9), (10)로 주어지는 이산 푸리에 변환(discrete Fourier transform)식은 f(x)가 주기함수일 때에만 성립하는 식이다. 원래의 입력신호 f(x)는 x = 0, 1, …, W-1의 유한 구간에서 정의된 함수이다. 우리가 관심있는 부분은 0 ~ W-1 구간에서의 특성이므로 그 외의 구간에 대해서는 함수를 어떻게 정의해도 무방하다. 따라서, 푸리에 변환 적용을 위해 이 함수를 확장하여 f(x + W) = f(x)인 주기함수(0 ~ W-1에서의 함수값이 다른 구간에서도 계속 반복)로 가정하고 식을 세운 것이 식 (9), (10)이다. 이 때, F(u) 또한 f(x)와 동일한 주기(W)의 주기함수가 된다. 즉. F(u) = F(u + W). 또한 식 (10)에서 |F(u)| = |F(-u)|임도 쉽게 알 수 있다. 즉, 이산 푸리에 스펙트럼은 원점대칭이면서 W를 주기로 하는 주기함수 형태임을 알 수 있다. 2차원의 경우도 마찬가지이며 F(u, v) = F(u + W, v) = F(u, v+ H) = F(u + W, v + h), |F(u, v)| = |F(-u, -v)|인 주기함수가 된다. 그리고 이러한 원점 대칭성과 주기성으로 인해 스펙트럼 이미지를 그림 3(c)와 같이 shift하여 표현하는 것이 가능해진다.

shifted 스펙트럼을 이해하기 위해 한 예로 아래 그림 4의 왼쪽과 같은 형태의 스펙트럼 신호를 생각해 보자. 그런데 만일 스펙트럼이 원점대칭이고 W를 주기로 반복된다면 푸리에 스펙트럼은 오른쪽과 같은 형태가 될 수밖에 없음을 알 수 있다. 원래의 푸리에 스펙트럼의 형태는 구간 0 ~ W의 형태(그림 3b)이지만 (어차피 정보가 반복되기 때문에) 이를 구간 -W/2 ~ W/2 형태(그림 3c)로 shift하여 표현한 것이 shifted 스펙트럼이다.

그림 4. 푸리에 스펙트럼의 주기 특징

B. 푸리에 스펙트럼의 해석

앞서 푸리에 스펙트럼(Fourier spectrum)은 해당되는 주파수 성분의 강도를 나타난다고 했는데, 정말 그런지 그리고 이 값이 이미지 도메인에서 어떻게 해석될 수 있는지 실제 예를 통해서 살펴보자.

아래 예는 이미지에 인위적으로 주기성분을 추가하였을 때 주파수 공간에서의 푸리에 스펙트럼이 어떻게 변하는지를 보여준다. 원본 이미지의 해상도는 205 × 205 픽셀이며(W = 205, H = 205) 따라서 스펙트럼 이미지도 205 x 205 해상도를 갖는다.

그림 5. 주기성분 추가에 따른 푸리에 스펙트럼의 변화

먼저, 그림 5(a)는 원본 이미지 및 대응되는 푸리에 스펙트럼 이미지를 보여준다. 그림의 예와 같이 일반적인 푸리에 스펙트럼 이미지는 원점 F(0, 0) 주변의 저주파 영역에서 강한 피크(peak)가 나타나고 원점에서 멀어질수록 즉, 고주파 영역으로 갈수록 값이 급격히 작아지는 형태를 갖는다.

그림 5(b)는 (a)의 이미지에 5 픽셀(pixel) 간격의 수평선을 인위적으로 추가한 경우이다. 그러면 주파수 공간에서는 그림과 같이 F(0, 41), F(0,82)에 강한 피크(peak)가 나타난다. 앞서 이산 푸리에 변환에서 F(u, v)는 x축 주기 W/u 픽셀, y축 주기 H/v 픽셀인 주기성분의 계수라 했다. 그러면, F(0, 41)은 주기가 x축 방향 205/0 = ∞, y축 방향 205/41 = 5 픽셀인 주기성분에 대응된다. 그리고 이것은 그림 5(b)를 만들 때 사용한 수평선의 주기(세로방향 5픽셀)와 정확히 일치한다.

☞ F(0, 82)에도 피크(peak)가 나타나는 것은 y축 방향으로 205/82 = 2.5 픽셀 간격의 주기 성분이 입력 이미지에 있다는 의미이다. 이는 이미지에 추가한 수평선이 정현파(sinusoidal wave)가 아니라 계단 형태이기 때문에 5 픽셀 주기의 정현파와 2.5 픽셀 주기의 정현파를 합쳐서 그러한 계단 형태를 근사했기 때문이다.

다음으로, 이번에는 그림 5(c)와 같이 대각선 방향의 정현파를 (a)의 이미지에 추가해 보자. 추가한 정현파는 x축 방향 주기 20 pixel, y축 방향 주기 10 픽셀인 2D sin 함수를 이용했다. 이 때, 푸리에 스펙트럼에는 F(10, 20.5)에 강한 피크(peak)가 생성됨을 확인할 수 있다. 즉, x축 방향으로는 W/u = 205/10 = 20.5 픽셀, y축 방향으로는 H/v = 205/20.5 = 10 픽셀의 주기 성분이 입력 이미지에 있음을 의미한다. 그리고 이는 실제 입력 이미지에 추가된 주기 성분과 정확히 일치한다 (소수점 오차는 u, v좌표를 정수로 표현함에 의한 것이다).

이상으로 주파수 공간에서의 F(u, v)가 입력 이미지 공간에서 어떻게 연관되어 해석될 수 있는지를 실제 예를 통해서 살펴보았다. 마지막으로 앞서 그림 5(b), (c)에서 스펙트럼의 피크(peak) 영역을 지운 후 푸리에 역변환(inverse Fourier transform)하면 아래와 같은 재미있는 결과를 얻을 수 있다 (지운다는 의미는 해당되는 F(u, v) 값들을 0으로 만든다는 의미이다).

그림 6. 푸리에 변환을 이용한 주기 성분 제거

☞ [개발한 것들] – FFT와 모아레 제거 프로그램을 이용하면 이미지의 푸리에 변환, 특정 스펙트럼 삭제 및 역변환을 직접 테스트해 볼 수 있다.

C. 푸리에 변환의 페이즈(phase)

푸리에 변환(Fourier transform)에서 스펙트럼(spectrum)은 잘 알려진 반면 페이즈(phase)는 상대적으로 잘 알려져 있지 않다. 하지만 페이즈(phase)에도 스펙트럼(spectrum) 못지 않은 중요한 정보가 담겨 있다고 한다.

페이즈(phase)를 우리말로 번역하면 ‘단계’가 되고 전문용어로는 ‘위상’이 된다. 위키피디아에는페이즈(phase, 위상)를 ‘반복되는 파형의 한 주기에서 첫 시작점의 각도 혹은 어느 한 순간의 위치’라고 정의한다. 즉, 파형(wave)의 시점이 어디인지가 페이즈(phase)이다. 예를 들어, sin 파와 cos 파는 90도의 페이즈(phase, 위상) 차이가 존재하는 동일한 파형으로 볼 수 있다.

푸리에 변환의 관점에서 보면 페이즈(phase)는 원본 신호를 주기 신호로 분해했을 때 각 주기성분의 시점이 어딘인지(즉, 각 주기성분들이 어떻게 줄을 맞춰서 원본 신호를 생성했는지)를 나타내는 요소가 된다.

아래 그림은 페이즈(phase)의 영향을 보여주는 예로서 파란색 주기성분 신호들을 합쳐서 빨간색 신호가 생성되는 예를 보여준다. 왼쪽, 오른쪽 경우 모두 동일한 주파수의 주기성분들을 합쳤지만 각 성분의 페이즈(phase) 차이로 인하여 전혀 다른 신호가 생성됨을 확인할 수 있다.

그림 7. 페이즈(phase) 차이에 따른 신호 생성의 차이

다음으로 푸리에 변환의 페이즈(phase)가 어떻게 수식으로 표현되는지 살펴보자. (1차원) 푸리에 변환의 계수 F(u)는 식 (12), (13) 및 오일러 공식에 의해 다음과 같이 극좌표(polar coordinate) 형태로 표현될 수 있다 (설명의 편의상 1차원의 경우를 예로 든다).

— (14)

☞ 실수축이 x축, 허수축이 y축인 복소평면에서 F(u)는 x축과 이루는 각이 Φ인 막대기의 끝점 (R, I)에 대응된다. 이 때, R = |F|cosΦ, I = |F|sinΦ이므로 F = |F|cosΦ + j|F|sinΦ = |F|ejΦ.

이제 식 (14)를 식 (1)에 대입하면,

. — (15)

와 같이 페이즈(phase) 텀이 주기함수 성분의 시점을 조절하는 텀이 된다.

즉, 푸리에 계수 F(u)에는 대응되는 주기함수 성분의 강도(amplitude)를 나타내는 스펙트럼 정보 |F(u)|와 시점을 조절하는 페이즈(phase) 정보 Φ(u)가 함께 포함되어 있음을 알 수 있다.

참고로, 푸리에 스펙트럼(spectrum)과 페이즈(phase)에 관한 재미있는 비교 결과를 하나 소개한다. 아래 그림 8에서 (a)는 원본 이미지, (b)는 푸리에 스펙트럼을 보존하고 페이즈(phase)를 랜덤(random)하게 했을 때의 역변환 결과, (c)는 페이즈(phase)를 보존하고 스펙트럼을 랜덤하게 했을 때의 역변환 결과이다. 결과를 보면 이미지의 푸리에 변환에서 스펙트럼(spectrum)보다 페이즈(phase)에 보다 더 중요한 정보가 포함되어 있음을 확인할 수 있다.

그림 8. 푸리에 스펙트럼과 페이즈의 중요도 비교

5. 푸리에 변환의 유용한 성질들

마지막으로 푸리에 변환(Fourier transform)에 대한 몇 가지 유용한 성질들을 정리하면 다음과 같다.

– 주파수 공간의 원점 F(0, 0)의 값은 이미지의 평균값과 일치

– Impulse 함수(Dirac delta 함수)에 대한 푸리에 변환/역변환은 유니폼(uniform) 함수 (아래 식에서 푸리에 변환/역변환 관계를 ⇔ 로 표기).

– 가우시언(Gaussian) 함수의 푸리에 변환/역변환은 가우시언 함수가 됨

6. 맺음말

이상으로 푸리에 변환(Fourier transform)에 대한 정리를 마칩니다. 원래는 이렇게까지 길게 쓸 생각은 아니없는데 쓰다 보니 글이 길어졌네요.. ^^

참고자료 및 유용한 관련 글 링크

푸리에 변환 by jipark

푸리에 급수의 시작 by 전파거북이

푸리에 변환 by 전파거북이

페이저(phasor) by AngeloYeo

허수의 존재 의미에 대하여 by AngeloYeo

Magnitude and Phase by Deepa Kundur (토론토 대학)

What information is contained in the phase spectrum of a signal?

by 다크 프로그래머

So you have finished reading the 푸리에 변환 그래프 topic article, if you find this article useful, please share it. Thank you very much. See more: 푸리에 변환 고등학교, 푸리에 변환 사이트, 푸리에 변환 예제, 푸리에 변환 프로그램, 푸리에 변환 공식 표, 푸리에 변환 풀이, 푸리에 변환 미분, 푸리에 변환 유도

Top 43 푸리에 변환 그래프 The 35 Correct Answer

05-2. 한 신호를 정해서 손으로 푸리에 변환 해보기

푸리에 변환에 대한 정확한 분석(Fourier Transform)

다크 프로그래머 :: Fourier Transform(푸리에 변환)의 이해와 활용

푸리에 변환(Fourier transform) (1) – 이해와 유도

푸리에 변환(Fourier Transform)
– MATLAB & Simulink
– MathWorks 한국

05-2. 한 신호를 정해서 손으로 푸리에 변환 해보기

푸리에 변환에 대한 정확한 분석(Fourier Transform)

다크 프로그래머 :: Fourier Transform(푸리에 변환)의 이해와 활용

Leave a Comment Cancel reply

05-2. 한 신호를 정해서 손으로 푸리에 변환 해보기

푸리에 변환에 대한 정확한 분석(Fourier Transform)

다크 프로그래머 :: Fourier Transform(푸리에 변환)의 이해와 활용

푸리에 변환(Fourier transform) (1) – 이해와 유도

푸리에 변환(Fourier Transform) – MATLAB & Simulink – MathWorks 한국

05-2. 한 신호를 정해서 손으로 푸리에 변환 해보기

푸리에 변환에 대한 정확한 분석(Fourier Transform)

다크 프로그래머 :: Fourier Transform(푸리에 변환)의 이해와 활용

Leave a Comment Cancel reply

푸리에 변환(Fourier Transform)
– MATLAB & Simulink
– MathWorks 한국