You are looking for information, articles, knowledge about the topic nail salons open on sunday near me 루트 2 무리수 증명 on Google, you do not find the information you need! Here are the best content compiled and compiled by the https://chewathai27.com/to team, along with other related topics such as: 루트 2 무리수 증명 루트5 무리수 증명, 루트3 무리수 증명, 루트n 무리수 증명, 루트 2 값, 루트2 무리수 귀납법, 무리수 증명 귀류법, 루트 2 무한, 루트 2의 루트 2 승
루트2는 무리수이다 증명 : 네이버 블로그
- Article author: m.blog.naver.com
- Reviews from users: 34575
Ratings
- Top rated: 3.0
- Lowest rated: 1
- Summary of article content: Articles about 루트2는 무리수이다 증명 : 네이버 블로그 고등학교 1학년 때 배우는 무리수 파트중 가장 중요한 부분 중 하나인. . “루트2는 무리수이다.”의 증명입니다. . 일단, 가장 기본적인 방법, … …
- Most searched keywords: Whether you are looking for 루트2는 무리수이다 증명 : 네이버 블로그 고등학교 1학년 때 배우는 무리수 파트중 가장 중요한 부분 중 하나인. . “루트2는 무리수이다.”의 증명입니다. . 일단, 가장 기본적인 방법, …
- Table of Contents:
카테고리 이동
수학과 전자공학
이 블로그
수학
카테고리 글
카테고리
이 블로그
수학
카테고리 글

[귀류법] 루트2가 무리수임을 증명. 무조건 이해되는 설명.
- Article author: ladyang86.tistory.com
- Reviews from users: 39884
Ratings
- Top rated: 3.4
- Lowest rated: 1
- Summary of article content: Articles about [귀류법] 루트2가 무리수임을 증명. 무조건 이해되는 설명. Updating …
- Most searched keywords: Whether you are looking for [귀류법] 루트2가 무리수임을 증명. 무조건 이해되는 설명. Updating 귀류법 : 명제의 부정이 맞다고 가정해서 모순임을 보이는 방법. 말이 어렵죠? 특히나 증명 과정에서 분수로 두고 정리하고.. 어렵습니다. 오늘은 이렇게 어려운 귀류법을 좀 쉽게 설명해보도록 할게요. 포스팅 다..30대 수학 강사입니다.
- Table of Contents:
티스토리툴바
![[귀류법] 루트2가 무리수임을 증명. 무조건 이해되는 설명.](https://img1.daumcdn.net/thumb/R800x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbGkqPH%2FbtqNnwZ66Lw%2Fa4F1INzhYeMIAQ9yqAV4ak%2Fimg.png)
무리수, 루트 2
- Article author: brunch.co.kr
- Reviews from users: 11288
Ratings
- Top rated: 3.9
- Lowest rated: 1
- Summary of article content: Articles about 무리수, 루트 2 무리수, 루트 2 · 루트2는 무리수? · 1.41421 35623 73095 04880 16887 24209 69807 85696 71875 37694 80731 76679 73799. …
- Most searched keywords: Whether you are looking for 무리수, 루트 2 무리수, 루트 2 · 루트2는 무리수? · 1.41421 35623 73095 04880 16887 24209 69807 85696 71875 37694 80731 76679 73799. :: 표현하지만, 표현할 수 없는 수 | 루트2는 무리수? 우리가 살면서 최소한 한 번쯤(중, 고등학생 시절) 혹은 그 이상 여러번 들어봤을 가능성이 조금은 있는 숫자라고 생각한다. 루트2. 아무 생각없이 내뱉으며 계산하
- Table of Contents:

제곱근 2 – 위키백과, 우리 모두의 백과사전
- Article author: ko.wikipedia.org
- Reviews from users: 28850
Ratings
- Top rated: 4.4
- Lowest rated: 1
- Summary of article content: Articles about 제곱근 2 – 위키백과, 우리 모두의 백과사전 제곱근 2 또는 루트 2 또는 2의 양의 제곱근은 자기 자신과 곱하여 2가 되는 양의 실수이다. … 로 표기한다. 2의 제곱근은 기약분수로 나타낼 수 없는 무리수이다. …
- Most searched keywords: Whether you are looking for 제곱근 2 – 위키백과, 우리 모두의 백과사전 제곱근 2 또는 루트 2 또는 2의 양의 제곱근은 자기 자신과 곱하여 2가 되는 양의 실수이다. … 로 표기한다. 2의 제곱근은 기약분수로 나타낼 수 없는 무리수이다.
- Table of Contents:
역사[편집]
계산[편집]
무리수 증명[편집]
주해[편집]
각주[편집]

루트 2 무리수 증명
- Article author: nous-temperature.tistory.com
- Reviews from users: 3041
Ratings
- Top rated: 3.9
- Lowest rated: 1
- Summary of article content: Articles about 루트 2 무리수 증명 루트 2 값을 계산하는 방법에 관해서 지난 시간에 알아보았는데, 이번 시간에는 루트 2가 무리수인 이유에 관해서 설명해 보고자 합니다. 보통 루트 2 … …
- Most searched keywords: Whether you are looking for 루트 2 무리수 증명 루트 2 값을 계산하는 방법에 관해서 지난 시간에 알아보았는데, 이번 시간에는 루트 2가 무리수인 이유에 관해서 설명해 보고자 합니다. 보통 루트 2 … 루트 2 값을 계산하는 방법에 관해서 지난 시간에 알아보았는데, 이번 시간에는 루트 2가 무리수인 이유에 관해서 설명해 보고자 합니다. 보통 루트 2가 무리수, 즉 유리수가 아니다는 정의는 다음과 같습니다…뒤를 보면 비로소 보이는 것들
- Table of Contents:
루트 2 무리수 증명
티스토리툴바
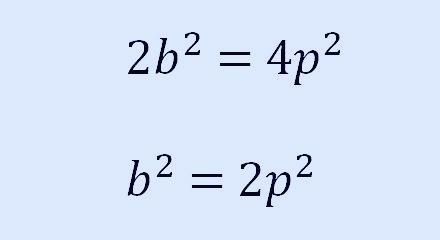
루트 2가 무리수임을 n가지 방법으로 증명해보기 :: 실버의 낙서장
- Article author: 16silver.tistory.com
- Reviews from users: 14913
Ratings
- Top rated: 3.1
- Lowest rated: 1
- Summary of article content: Articles about 루트 2가 무리수임을 n가지 방법으로 증명해보기 :: 실버의 낙서장 기본적으로는, 유리수라는 걸 가정하고, 어찌어찌하다가, 모순을 이끌어내서 유리수라는 가정이 틀렸다는 것으로부터 \(\sqrt{2}\)가 무리수임이 증명된다 … …
- Most searched keywords: Whether you are looking for 루트 2가 무리수임을 n가지 방법으로 증명해보기 :: 실버의 낙서장 기본적으로는, 유리수라는 걸 가정하고, 어찌어찌하다가, 모순을 이끌어내서 유리수라는 가정이 틀렸다는 것으로부터 \(\sqrt{2}\)가 무리수임이 증명된다 … 루트 2(\(\sqrt{2}\))가 무리수임을 처음 배우는 것은 중학교 3학년 때이다(’19 기준). 그 증명을 기억하는가? 기본적으로는, 유리수라는 걸 가정하고, 어찌어찌하다가, 모순을 이끌어내서 유리수라는 가정이 틀렸..
- Table of Contents:
루트 2가 무리수임을 n가지 방법으로 증명해보기
1 간단한 증명
2 소인수분해의 유일성을 이용한 증명
3 무한강하법을 이용한 증명 1
4 무한강하법을 이용한 증명 2
5 최대공약수 정리를 이용한 풀이

루트2는 무리수이다 – 수학노트
- Article author: wiki.mathnt.net
- Reviews from users: 34311
Ratings
- Top rated: 4.6
- Lowest rated: 1
- Summary of article content: Articles about 루트2는 무리수이다 – 수학노트 도 수다. 증명. √2를 유리수라 한다면, 분수 꼴의 형태로 나타낼 수 있다. 임의의 정수 … …
- Most searched keywords: Whether you are looking for 루트2는 무리수이다 – 수학노트 도 수다. 증명. √2를 유리수라 한다면, 분수 꼴의 형태로 나타낼 수 있다. 임의의 정수 …
- Table of Contents:
목차
개요
증명
역사
관련된 항목들
관련도서
관련논문
관련기사
둘러보기 메뉴

See more articles in the same category here: https://chewathai27.com/to/blog.
루트2는 무리수이다 증명
루트2는 무리수이다 증명
고등학교 1학년 때 배우는 무리수 파트중 가장 중요한 부분 중 하나인
“루트2는 무리수이다.”의 증명입니다.
일단, 가장 기본적인 방법, 제가 고등학교 다닐 때 교과서에 나왔던 방법입니다.
는 유리수가 아니다.
-> 는 유리수이다. (귀류법을 사용합니다. 귀류법이란 증명하고자 하는 명제의 진위를 가정해서 모순을 이끌어 내는 증명법입니다.)
는 유리수 이므로 다음을 만족하는 정수 a,b가 존재 한다.
양변을 제곱하고 정리를 하면
은 짝수 이므로 도 짝수이다.
이 짝수 이므로 도 짝수이다.
그러므로 로 나타낼수 있다.
을 에 대입하면 이 성립한다.
이 짝수 이므로 도 짝수이다.
이 짝수이므로 도 짝수이다.
와 가 짝수이므로 , 는 서로소가 아니다.
따라서 ” , 는 서로소”와 모순이다.
즉, 는 유리수가 아니다.
두번째 방법은 제가 여러책을 읽으면서 여러 증명을 봤는데. 고등학교 때 수행평가에 이게 나와서 서로소라는 말을 안적고 푸는 방법을 적었다가 선생님이 다른 답인줄 모르고 틀렸다고 했었던 증명이라 적어봅니다.
서로소를 사용하지 않고 풀어보겠습니다.
방법은 위와 비슷합니다. 귀류법을 상용합니다.
는 유리수 이므로 다음을 만족하는 정수 a,b가 존재 한다. 양변을 제곱하고 정리를 하면
제곱을 소인수분해를 할 경우 각각의 소인수들이 짝수개가 나오게 됩니다.
좌변과 우변을 비교해봅니다.
그러면 좌변에는 2가 홀수개(짝수+1=홀수), 우변은 짝수개가 나오게됩니다.
소인수 분해의 일의성에 따라 좌변과 우변의 소인수의 개수는 소인수별로 모두 일치해야합니다.
따라서, 루트2가 유리수라는 가정은 모순이 됩니다.
[귀류법] 루트2가 무리수임을 증명. 무조건 이해되는 설명.
반응형
귀류법 : 명제의 부정이 맞다고 가정해서 모순임을 보이는 방법.
말이 어렵죠? 특히나 증명 과정에서 분수로 두고 정리하고.. 어렵습니다. 오늘은 이렇게 어려운 귀류법을 좀 쉽게 설명해보도록 할게요. 포스팅 다 읽을 때 쯤이면 증명도 하고 있는 나의 모습을 발견할 수 있을 거에요!
루트2가 무리수인걸 직접 보이기는 어렵습니다.
왜냐면 무리수는 순환하지 않는 무한소수거든요.
순환하지 않는 무한소수인걸 직접 보이려면… 엄.. 무한히 가는 숫자인걸 직접 보여줘야 하는데.. 말이 안되죠?
그럼 어떻게 할까 고민해봅시다. 여기서 사용되는 게 귀류법입니다.
유리수라 했더니 말이 안됨. 유리수 아니니까 무리수임! 이렇게 증명하는 것이죠.
이런 상황을 생각해봅시다.
어느날 내가 살인자로 몰렸다. 경찰이 내가 유력한 용의자라며 살인자가 아닌 걸 증명하라고 했다.
아니.. 슈밤.. 아닌 걸 어떻게 증명해.
그래서 나는 이렇게 말했다.
형사 아저씨, 내가 만약 살인자라고 가정해봅시다. 그런데 저는 그 시간에 수업을 하고 있었다구요. 여기여기 증거와 증인이 있어요. 형사 아저씨 말대로 제가 살인자라고 하면 말이 안되죠? 그러니 저는 결백해요.ㅇㅋ?
이런 과정이 귀류법입니다.
나는 무죄다. 근데 결백하다는 걸 직접 증명하는 건 힘드니, 너의 주장대로 내가 범인이라고 가정해보자. 근데 그러면 모순이 나온다. 즉, 내가 범인이라면 말이 안되니까 나는 무죄다. 라고 증명하는 게 귀류법인거죠.
다시 원래의 증명법으로 돌아가봅시다.
루트2가 무리수임을 증명하라!!
무리수는 순환하지 않는 무한 소수죠.
아니.. 그럼 나눠서 무한히 나오는 걸 증명해야 하잖아?
말이 안됩니다. 그러니, 무리수가 아니라고 하면(유리수라고 가정하면) 말이 안되니까(모순이니까) 참임을 보입시다.
루트2가 유리수라고 가정하자.
그럼 서로소인 분수로 표현이 된다.
근데 정리해보니 서로소가 아니네?
이건 앞에서 서로소라고 말한거에 모순이다.
그러니까 유리수가 아니다.
이런 과정입니다.
이제 이걸 식으로 써봅시다.
이제부터 식을 정리해보니 서로소가 아니라는 걸 보여줄겁니다.
그러니 반드시 처음에 a,b는 서로소인 정수라고 가정해야
나중에 모순이라고 말할 수 있겠죠?
이제는 식을 정리하는 과정에서 서로 2의 배수라는걸 보여줄 거에요.
정리를 해보니 b가 2의 배수로 나왔네요. 그죠?
아까 a,b는 서로소라고 가정했는데 둘 다 짝수가 나왔군요. 말이 안됩니다. 모순이죠.
즉, 유리수라고 가정했는데 말이 안되므로 무리수입니다.
루트3이나 루트5의 경우도 마찬가지로 증명하시면 됩니다. 유리수라고 가정하면 서로소인 정수의 비로 나타낼 수 있는데, 식을 정리해보니 둘 다 3의 배수/5의 배수가 나와서 서로소에 모순이라고 보는 것이죠.
이해가 잘 되셨나요?
이 부분은 명확한 식까지 처음에 다 못외운다면, 큰 흐름이라도 먼저 보시는 게 좋습니다.
그럼 다음에도 쉬운 설명 들고 올게요~!
반응형
무리수, 루트 2
루트2는 무리수?
우리가 살면서 최소한 한 번쯤(중, 고등학생 시절) 혹은 그 이상 여러번 들어봤을 가능성이 조금은 있는 숫자라고 생각한다. 루트2. 아무 생각없이 내뱉으며 계산하는 숫자이기도 하고, 솔직히 살면서 거의 사용할 일도 거의 없고 관심이 있는 사람도 극소수인 건 사실이다. 그럼에도 불구하고 오늘 루트2에 대해서 한 번 얘기를 해보려 한다.
먼저 제곱근을 알아야 한다. 제곱근이란 어떤 수 a가 존재할 때, 제곱하여 a가 되는 수를 제곱근이라고 한다. 일반적으로 양의 실수 a의 제곱근은 두 개가 존재한다(양의 제곱근, 음의 제곱근). 오늘 함께 나눌 루트2는 따라서 2의 제곱근이 되는 것이다(루트2를 제곱하면 2가 되므로).
루트 x
2의 제곱근인 루트2는 기약분수로 나타낼 수 없는 무리수이다. 기하학에서 피타고라스 정리에 따르면 한 변의 길이가 1인 정사각형의 대각선의 길이로 루트2를 나타낼 수 있다. 루트2에 대한 근사값으로는 99/70이 쓰인다. 이 값은 2의 제곱근 참값과의 사이에 오차가 0.00001로 매우 정확한 표현법이다. 실제 2의 제곱근 값은 순환되지 않는 무한소수로 소수점 이하 65자리까지의 근사값(OEIS 수열 A002193)은 다음과 같다.
1.41421 35623 73095 04880 16887 24209 69807 85696 71875 37694 80731 76679 73799
2의 제곱근이 무리수라는 사실은 고대 그리스 시기부터 잘 알려져 있다. 에우클레이데스는 <원론>에서 2의 제곱근이 무리수라는 사실을 *귀류법을 통하여 증명하였다.
귀류법 : 어떤 명제를 증명하고자할 때, 그 명제의 결론을 부정함으로써 공리의 모순됨을 보여 간접적으로 결론이 참임을 증명하는 방법
바빌로니아 점토판에서의2의 제곱근 근삿값
예일대학교 소장목록 7289인 바빌로니아 점토판에는 2의 제곱근의 근삿값을 다음과 같이 계산하고 있다.
고대 인도 시대 2의 제곱근계산법
또한 고대 인도의 수학책 <술바수트라>에서는 2의 제곱근의 근삿값을 다음과 같이 계산하고 있다.
직각삼각형에서 빗변의 길이를 Z, 다른 변의 길이를 각각 X, Y라고 하면,
피타고라스 정리에 따라 다음과 같은 식이 성립한다. 이제 빗변이 아닌 두 변의 길이가 1인 직각 삼각형의 빗변의 길이를 계산할 수 있다.
피타고라스 정리에 의한 빗변이 아닌 두 변의 길이가 각각 1일 때, 빗변의 길이 계산
고대 그리스 수학자 피타고라스 학파인 히파수스는 이 계산에서 나타나는 2의 제곱근을 기약분수로 나타낼 수 없다는 사실을 발견하였다. 그런데 피타고라스 학파에서는 자연수와 이의 비로 나타낼 수 있는 기약분수, 즉 유리수만을 진정한 수로 취급하였기 때문에 무리수의 존재를 인정하지 않았고, 무리수를 인정하는 것은 금기로 여겨졌다. 히파수스는 무리수의 존재를 세상에 알렸다는 이유로 이단 취급을 받았으며, 일설에 의하면 피타고라스 학파에 의해 죽임을 당하였다고 한다. 무리수라는 이름은 피타고라스 학파의 수에 대한 이러한 가치관이 반영된 것이다.
반면, 헬레니즘 시기 알렉산드리아의 수학자 에우클레이데스는 2의 제곱근이 무리수라는 것을 증명하였다. 에우클레이데스는 <원론>에서 귀류법을 이용하여 2의 제곱근이 무리수라는 것을 증명하였는데, 그 증명과정은 다음과 같다.
수학자 히파수스는 그 당시까지만 해도 루트2라는 길이를 그 어떤 수로도 나타낼 수 없음을 증명하였다. 그것은 새로운 수의 세계가 존재한다는 얘기였다. 우리도 어쩌면 표현할 수 없는 새로운 수의 세계 안에 살고 있는 것은 아닐까?
So you have finished reading the 루트 2 무리수 증명 topic article, if you find this article useful, please share it. Thank you very much. See more: 루트5 무리수 증명, 루트3 무리수 증명, 루트n 무리수 증명, 루트 2 값, 루트2 무리수 귀납법, 무리수 증명 귀류법, 루트 2 무한, 루트 2의 루트 2 승

