Hoe De Schuine Zijde Berekenen Met Hoek: Eenvoudige Formules En Handige Tips
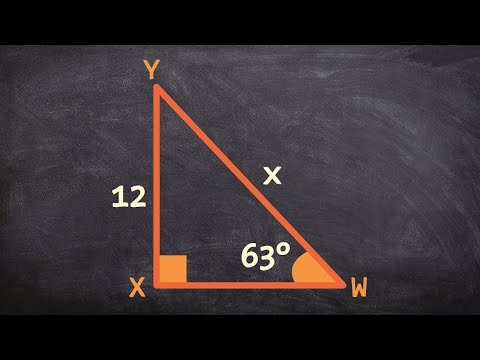
Using The Sine Function To Find The Missing Length Of The Hypotenuse
Keywords searched by users: schuine zijde berekenen met hoek schuine zijde berekenen online, hoek berekenen calculator, schuine zijde driehoek berekenen, driehoek berekenen met 1 zijde en 1 hoek, zijde berekenen met tangens, rechte zijde driehoek berekenen, stelling van pythagoras rechte zijde berekenen, overstaande zijde berekenen
Schuine zijde berekenen met hoek: Een complete gids
Inleiding
In de wiskunde worden driehoeken vaak gebruikt om verschillende concepten en berekeningen te illustreren. Een belangrijk aspect van driehoeken is het berekenen van de zijden, vooral de schuine zijde, met behulp van de gegeven hoek. In dit artikel zullen we ons richten op het berekenen van de schuine zijde van een driehoek met behulp van een gegeven hoek en verschillende methoden om dit te doen.
Wat is een schuine zijde?
Een driehoek heeft drie zijden: de basis, de hoogte en de schuine zijde. De schuine zijde is de zijde die niet loodrecht staat op de basis. Het verbindt de twee niet-rechthoekige hoeken van de driehoek en is de langste zijde in een rechthoekige driehoek.
De relatie tussen de schuine zijde en de hoek
De schuine zijde en de hoek hebben een nauwe relatie in een rechthoekige driehoek. Volgens de stelling van Pythagoras kan de lengte van de schuine zijde worden berekend op basis van de lengtes van de andere twee zijden. Deze relatie is essentieel bij het berekenen van de schuine zijde met behulp van een gegeven hoek.
Hoe bereken je de schuine zijde met behulp van een gegeven hoek?
Om de schuine zijde te berekenen met behulp van een gegeven hoek, moeten we gebruik maken van de trigonometrische verhoudingen: sinus, cosinus en tangens.
1. Sinus (sin): de sinus van een hoek is gedefinieerd als de verhouding tussen de lengte van de overstaande zijde en de lengte van de schuine zijde. De formule om de schuine zijde te berekenen met behulp van de sinus is:
schuine zijde = overstaande zijde / sin(gegeven hoek)
2. Cosinus (cos): de cosinus van een hoek is gedefinieerd als de verhouding tussen de lengte van de aanliggende zijde en de lengte van de schuine zijde. De formule om de schuine zijde te berekenen met behulp van de cosinus is:
schuine zijde = aanliggende zijde / cos(gegeven hoek)
3. Tangens (tan): tangens van een hoek is gedefinieerd als de verhouding tussen de lengte van de overstaande zijde en de lengte van de aanliggende zijde. De formule om de schuine zijde te berekenen met behulp van de tangens is:
schuine zijde = overstaande zijde / tan(gegeven hoek)
De stelling van Pythagoras
Een andere methode om de schuine zijde te berekenen met behulp van een gegeven hoek is door gebruik te maken van de stelling van Pythagoras. Deze stelling stelt dat in een rechthoekige driehoek het kwadraat van de schuine zijde gelijk is aan de som van de kwadraten van de andere twee zijden.
De formule die je kunt gebruiken om de schuine zijde te berekenen met behulp van de stelling van Pythagoras is:
schuine zijde = √(lengte basis^2 + lengte hoogte^2)
Rekenvoorbeelden
Laten we nu een paar rekenvoorbeelden bekijken om de berekening van de schuine zijde met behulp van een gegeven hoek beter te begrijpen.
Voorbeeld 1:
Stel dat we een rechthoekige driehoek hebben met een basis van 3 meter en een hoogte van 4 meter. We willen de lengte van de schuine zijde berekenen.
Volgens de stelling van Pythagoras:
schuine zijde = √(3^2 + 4^2)
schuine zijde = √(9 + 16)
schuine zijde = √25
schuine zijde = 5 meter
Voorbeeld 2:
Laten we nu een voorbeeld bekijken waarin we de tangens gebruiken om de schuine zijde te berekenen. Stel dat we een hoek van 30 graden hebben en een overstaande zijde van 5 meter. We willen de lengte van de schuine zijde vinden.
schuine zijde = overstaande zijde / tan(gegeven hoek)
schuine zijde = 5 / tan(30)
schuine zijde ≈ 8.66 meter
Andere methoden om de schuine zijde te berekenen
Naast de hierboven genoemde methoden zijn er nog andere manieren om de schuine zijde te berekenen. Als je bijvoorbeeld de waarden van de andere twee zijden kent, kun je de derde zijde berekenen met behulp van de stelling van Pythagoras.
Er zijn ook online hulpmiddelen en calculators beschikbaar die je kunnen helpen bij het berekenen van de schuine zijde met behulp van een gegeven hoek. Deze tools maken gebruik van de bovenstaande formules en vergemakkelijken het berekeningsproces.
Praktische toepassingen
Het berekenen van de schuine zijde van een driehoek met behulp van een gegeven hoek is nuttig in verschillende vakgebieden en dagelijkse situaties. Hier zijn enkele praktische toepassingen:
– Architectuur: Bij het ontwerpen van gebouwen en constructies is het belangrijk om de lengte van de schuine zijde te kennen, vooral bij het construeren van schuine daken.
– Techniek: In de mechanica en machinebouw wordt het berekenen van de schuine zijde met behulp van een gegeven hoek vaak toegepast bij het ontwerpen en analyseren van mechanische systemen.
– Bouw: Bij het construeren van trappen, hellingen en hellende oppervlakken is het berekenen van de schuine zijde met behulp van een gegeven hoek essentieel om de juiste afmetingen en hoeken te bepalen.
– Navigatie: In navigatietoepassingen, zoals landmeting en cartografie, wordt het berekenen van schuine zijden vaak gebruikt om afstanden en hoogteverschillen te bepalen.
Samenvatting
Het berekenen van de schuine zijde van een driehoek met behulp van een gegeven hoek is een belangrijk concept in de wiskunde en wordt toegepast in verschillende disciplines. Door gebruik te maken van formules zoals sinus, cosinus, tangens en de stelling van Pythagoras, kunnen we de lengte van de schuine zijde bepalen. Het begrijpen van deze methoden is essentieel bij het ontwerpen, construeren en analyseren van structuren en systemen.
Of je nu een student bent die wiskunde studeert, een professional in de techniek, bouw of architectuur, of gewoon iemand die geïnteresseerd is in het begrijpen van driehoeken, het berekenen van de schuine zijde met behulp van een gegeven hoek is een waardevolle vaardigheid die je kan helpen bij tal van taken en toepassingen.
Veelgestelde vragen
1. Kan ik de schuine zijde berekenen zonder de hoek te kennen?
Nee, om de schuine zijde te berekenen, moet je minstens één hoek kennen, samen met de lengtes van de andere zijden.
2. Kan ik een schuine zijde berekenen als ik maar één zijde ken?
Nee, om de schuine zijde te berekenen heb je minstens twee zijden nodig, inclusief de overstaande zijde van de gegeven hoek.
3. Zijn er online tools om de schuine zijde te berekenen met behulp van een gegeven hoek?
Ja, er zijn verschillende online calculators beschikbaar die je kunnen helpen bij het berekenen van de schuine zijde met behulp van een gegeven hoek. Je kunt deze tools vinden door te zoeken naar “schuine zijde berekenen online” of “hoek berekenen calculator” in een zoekmachine.
4. Kan ik de schuine zijde van elke driehoek berekenen met behulp van de hierboven genoemde methoden?
Nee, de hierboven genoemde methoden zijn specifiek voor rechthoekige driehoeken. Voor niet-rechthoekige driehoeken moeten andere methoden, zoals de sinusregel of de cosinusregel, worden toegepast.
5. Zijn er specifieke voorwaarden waaraan de gegeven hoek moet voldoen om de schuine zijde te kunnen berekenen?
Ja, de gegeven hoek moet de rechthoekige hoek zijn in een rechthoekige driehoek voor de formules en methoden zoals de stelling van Pythagoras, sinus, cosinus en tangens om van toepassing te zijn.
6. Kan ik de schuine zijde berekenen als ik de lengtes van de andere twee zijden ken?
Ja, je kunt de schuine zijde berekenen met behulp van de stelling van Pythagoras als je de lengtes van de andere twee zijden kent.
7. Zijn er andere manieren om de schuine zijde te berekenen?
Ja, naast de methoden die in dit artikel zijn genoemd, zijn er andere methoden, zoals de sinusregel en de cosinusregel, die kunnen worden toegepast om de schuine zijde te berekenen in niet-rechthoekige driehoeken.
8. Kan ik de schuine zijde van een driehoek meten met een meetlint?
Ja, je kunt de schuine zijde van een driehoek meten met een meetlint door het lint langs de zijde te plaatsen en de lengte te meten. Het is echter belangrijk om ervoor te zorgen dat het meetlint recht op de zijde staat om een nauwkeurige meting te krijgen.
9. Wordt de schuine zijde altijd aangegeven als “c” in een rechthoekige driehoek?
Nee, de schuine zijde kan worden aangegeven met verschillende letters, afhankelijk van de notatie die wordt gebruikt. Het is echter gebruikelijk om de langste zijde aan te duiden als “c” in de context van de stelling van Pythagoras.
10. Zijn de formules voor het berekenen van de schuine zijde van een driehoek met een gegeven hoek hetzelfde in elke wiskundige notatie?
Ja, de formules blijven hetzelfde in verschillende wiskundige notaties. De relatie tussen de schuine zijde, de overstaande zijde, de aanliggende zijde en de gegeven hoek blijft consistent, ongeacht de notatie die wordt gebruikt.
Categories: Delen 50 Schuine Zijde Berekenen Met Hoek
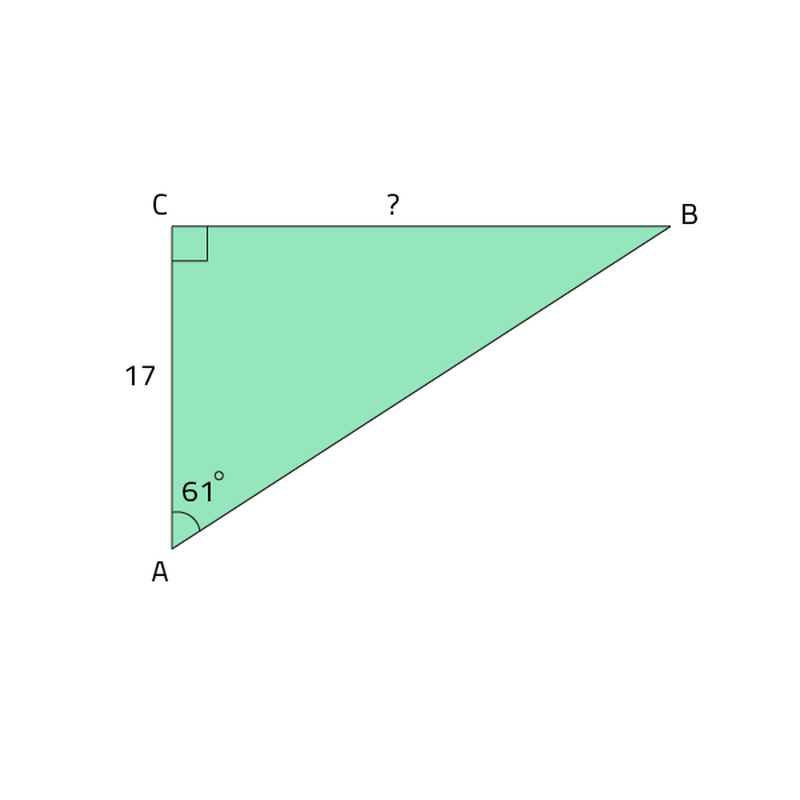
De formule die je kan gebruiken om de schuine en lange zijde van een driehoek te berekenen is c = √(a² + b²). Deze formule werkt alleen met rechthoekige driehoeken met een hoek van 90 graden.Een rechthoekige driehoek heeft 3 zijdes: 2 rechthoekszijden en een schuine zijde. De schuine zijde wordt ook wel eens de langste zijde, of de hypotenusa genoemd. Bij de stelling van Pythagoras kan je de schuine zijde berekenen wanneer je de 2 rechthoekszijden weet. De stelling wordt vaak aangegeven als a2 + b2 = c2.Methode. Of ook wel bekend als: a2 + b2 = c2, waarbij a en b de rechthoekszijden zijn en c de schuine zijde is. . De stelling van Pythagoras voor deze driehoek is AB2 + AC2 = BC2.
Hoe Bereken Je Schuine Zijde Uit?
Hoe Bereken Je Een Onbekende Zijde?
Hoe Kan Je De Hoeken Van Een Driehoek Berekenen?
Hoe Weet Je Wat Een Zijde Van Een Driehoek Is?
Delen 50 schuine zijde berekenen met hoek






See more here: chewathai27.com/to
Learn more about the topic schuine zijde berekenen met hoek.
- Schuine zijde driehoek berekenen – Hypotenusa Calculator
- Basis 1 – zijden berekenen met de sinus, cosinus en tangens
- Hoe Werkt de Stelling van Pythagoras? (Uitleg + Voorbeelden)
- Berekeningen met de Stelling van Pythagoras – Slimleren
- Driehoeksmeting | Math4All
- Zijden benoemen van rechthoekige driehoeken – Slimleren
See more: https://chewathai27.com/to/over-de-nos

