Top 50 Xor 문제 The 14 Correct Answer

You are looking for information, articles, knowledge about the topic nail salons open on sunday near me xor 문제 on Google, you do not find the information you need! Here are the best content compiled and compiled by the https://chewathai27.com/to team, along with other related topics such as: xor 문제 XOR 문제 해결, 다층 퍼셉트론 예제, 단층퍼셉트론, 다층 퍼셉트론 딥러닝 차이, 퍼셉트론 가중치 계산

XOR 문제는 논리 회로에 등장하는 개념입니다. 컴퓨터는 두 가지의 디지털 값, 즉 0과 1을 입력해 하나의 값을 출력하는 회로가 모여 만들어지는데, 이 회로를 ‘게이트(gate)’라고 부릅니다.

[머신러닝 강의 18] 머신러닝 XOR 문제

[인공지능]다층 퍼셉트론으로 XOR문제 해결하기

Article author: ang-love-chang.tistory.com
Reviews from users: 31511 Ratings
Top rated: 4.7
Lowest rated: 1
Summary of article content: Articles about [인공지능]다층 퍼셉트론으로 XOR문제 해결하기 Updating …
Most searched keywords: Whether you are looking for [인공지능]다층 퍼셉트론으로 XOR문제 해결하기 Updating 이 책에 있는 내용을 정리 한 것임. 모두의 딥러닝 개정2판: 3 코딩으로 XOR 문제 해결하기 – 4 thebook.io 2 퍼셉트론의 과제 사람의 뇌가 작동하는 데 1,000억 개나 되는 뉴런이 존재해야 하는 이유는 하나의 뉴..
Table of Contents:

7장 다층 퍼셉트론

‘인공지능’ Related Articles

Article author: trendy00develope.tistory.com
Reviews from users: 37703 Ratings
Top rated: 3.7
Lowest rated: 1
Summary of article content: Articles about [#E10] 딥러닝의 기초 XOR 문제란? [#E10] 딥러닝의 기초 XOR 문제란? 001+ 2018. 12. 8. 18:17. DEEP LEARNING은 기본적으로 NEURAL NETWORK(NN)를 기반으로 하며, 머신러닝을 더욱 완전하게 만드는 … …
Most searched keywords: Whether you are looking for [#E10] 딥러닝의 기초 XOR 문제란? [#E10] 딥러닝의 기초 XOR 문제란? 001+ 2018. 12. 8. 18:17. DEEP LEARNING은 기본적으로 NEURAL NETWORK(NN)를 기반으로 하며, 머신러닝을 더욱 완전하게 만드는 … DEEP LEARNING은 기본적으로 NEURAL NETWORK(NN)를 기반으로 하며, 머신러닝을 더욱 완전하게 만드는 방법으로 볼 수 있습니다. 아래의 그림은 x1과 x2 값에 따른 y의 값을 유동적으로 나타내고 있습니다. 그림..
Table of Contents:

태그

‘파이썬머신러닝’ Related Articles

Article author: stellarway.tistory.com
Reviews from users: 48318 Ratings
Top rated: 4.4
Lowest rated: 1
Summary of article content: Articles about XOR 문제의 해결, 층 쌓기 목차. XOR 문제 리마인트; XOR 문제 해결; 다층 퍼셉트론 (multi-layer perceptron). 1. XOR 문제 리마인드. 지난 포스트에서, 풀기 어려운 난제에 … …
Most searched keywords: Whether you are looking for XOR 문제의 해결, 층 쌓기 목차. XOR 문제 리마인트; XOR 문제 해결; 다층 퍼셉트론 (multi-layer perceptron). 1. XOR 문제 리마인드. 지난 포스트에서, 풀기 어려운 난제에 … 목차 XOR 문제 리마인트 XOR 문제 해결 다층 퍼셉트론 (multi-layer perceptron) 1. XOR 문제 리마인드 지난 포스트에서, 풀기 어려운 난제에 대해 이야기한 바가 있다. 문제를 풀기에 앞서, 문제가 무엇인지 리마..다각적 연구 노트 | NLP
Table of Contents:

Article author: wonryeol-study-code.tistory.com
Reviews from users: 38620 Ratings
Top rated: 4.9
Lowest rated: 1
Summary of article content: Articles about 딥러닝 01 – 기초 정리 XOR 문제 해결 과정 XOR 문제는 0 1 일때 True 값, 0 0 일때 False 값을 출력하는 컴퓨터 연산자인데, 상단의 그래프에 어떠한 선을 그어도 절대 XOR 개념에 만족하는 선 … …
Most searched keywords: Whether you are looking for 딥러닝 01 – 기초 정리 XOR 문제 해결 과정 XOR 문제는 0 1 일때 True 값, 0 0 일때 False 값을 출력하는 컴퓨터 연산자인데, 상단의 그래프에 어떠한 선을 그어도 절대 XOR 개념에 만족하는 선 … 머신러닝 개념이 발전하던 도중 중요한 문제점이 하나 발견이 되었다. 그 문제점은 어떻게 XOR 문제를 해결할 것인가? 라는 문제이다. XOR 문제는 0 1 일때 True 값, 0 0 일때 False 값을 출력하는 컴퓨터 연산자..
Table of Contents:

태그

공지사항

최근글

[인공지능]다층 퍼셉트론으로 XOR문제 해결하기

이 책에 있는 내용을 정리 한 것임.

2 퍼셉트론의 과제

사람의 뇌가 작동하는 데 1,000억 개나 되는 뉴런이 존재해야 하는 이유는 하나의 뉴런만으로는 아무것도 할 수 없기 때문입니다. 퍼셉트론도 마찬가지입니다. 단 하나의 퍼셉트론으로는 많은 것을 기대할 수가 없습니다. 지금부터는 퍼셉트론의 한계와 이를 해결하는 과정을 보며 신경망의 기본 개념을 확립해 보겠습니다. 먼저 그림 6-2를 볼까요?

그림 6-2

사각형 종이에 놓인 검은점 두 개와 흰점 두 개

사각형 종이에 검은점 두 개와 흰점 두 개가 놓여 있습니다. 이 네 점 사이에 직선을 하나 긋는다고 합시다. 이때 직선의 한쪽 편에는 검은점만 있고, 다른 한쪽에는 흰점만 있게끔 선을 그을 수 있을까요?

그림 6-3

선으로는 같은 색끼리 나눌 수 없다: 퍼셉트론의 한계

여러 개의 선을 아무리 그어보아도 하나의 직선으로는 흰점과 검은점을 구분할 수 없습니다.

앞서 배운 선형 회귀와 로지스틱 회귀를 통해 머신러닝이 결국 선이나 2차원 평면을 그리는 작업이란 것을 배웠습니다. 따라서 이와 같은 개념인 퍼셉트론 역시 선을 긋는 작업이라고 할 수 있습니다. 그런데 이 예시처럼 경우에 따라서는 선을 아무리 그어도 해결되지 않는 상황이 있습니다.

3 XOR 문제

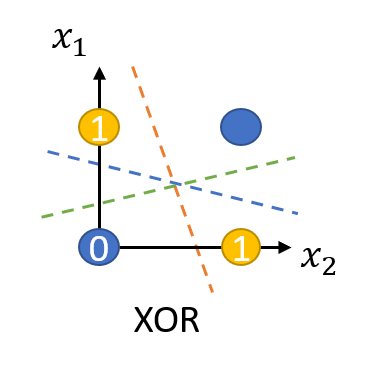
이것이 퍼셉트론의 한계를 설명할 때 등장하는 XOR(exclusive OR) 문제입니다.

XOR 문제는 논리 회로에 등장하는 개념입니다. 컴퓨터는 두 가지의 디지털 값, 즉 0과 1을 입력해 하나의 값을 출력하는 회로가 모여 만들어지는데, 이 회로를 ‘게이트(gate)’라고 부릅니다.

표 6-1은 AND 게이트, OR 게이트 그리고 XOR 게이트에 대한 값을 정리한 것입니다. AND 게이트는 x1와 x2 둘 다 1일 때 결괏값이 1로 출력됩니다. OR 게이트는 둘 중 하나라도 1이면 결괏값이 1로 출력됩니다. XOR 게이트는 둘 중 하나만 1일 때 1이 출력됩니다.

AND 진리표 OR 진리표 XOR 진리표 x1 x2 결괏값 x1 x2 결괏값 x1 x2 결괏값 0 0 0 0 0 0 0 0 0 0 1 0 0 1 1 0 1 1 1 0 0 1 0 1 1 0 1 1 1 1 1 1 1 1 1 0

표 6-1

AND, OR, XOR 게이트에 대한 진리표

표 6-1을 각각 그래프로 좌표 평면에 나타내 보겠습니다. 결괏값이 0이면 흰점으로, 1이면 검은점으로 나타낸 후 조금 전처럼 직선을 그어 위 조건을 만족할 수 있는지 보겠습니다.

그림 6-4

AND, OR, XOR 진리표대로 좌표 평면에 표현한 뒤 선을 그어 색이 같은 점끼리 나누기(XOR은 불가능)

AND와 OR 게이트는 직선을 그어 결괏값이 1인 값(검은점)을 구별할 수 있습니다. 그러나 XOR의 경우 선을 그어 구분할 수 없습니다.

이는 인공지능 분야의 선구자였던 MIT의 마빈 민스키(Marvin Minsky) 교수가 1969년에 발표한 <퍼셉트론즈(Perceptrons)>라는 논문에 나오는 내용입니다. ‘뉴런 → 신경망 → 지능’이라는 도식을 따라 ‘퍼셉트론 → 인공 신경망 → 인공지능’이 가능하리라 꿈꾸던 당시 사람들은 이것이 생각처럼 쉽지 않다는 사실을 깨닫게 됩니다. 알고 보니 간단한 XOR 문제조차 해결할 수 없었던 것입니다. 이 논문 이후 인공지능 연구가 한동안 침체기를 겪게 됩니다. 10여 년이 지난 후에야 이 문제가 해결되는데, 이를 해결한 개념이 바로 다층 퍼셉트론(multilayer perceptron)입니다.

7장 다층 퍼셉트론

앞서 종이 위에 각각 엇갈려 놓인 검은점 두 개와 흰점 두 개를 하나의 선으로는 구별할 수 없다는 것을 살펴보았습니다. 언뜻 보기에 해답이 없어 보이는 이 문제를 해결하려면 새로운 접근이 필요합니다.

어릴 적 친구들에게 장난처럼 들었던 문제인데 의외로 기발한 해답에 기억에 오래 남는 것이 하나 있습니다. 바로 ‘성냥개비 여섯 개로 정삼각형 네 개를 만들 수 있는가’라는 문제였습니다.

그림 7-1

성냥개비 여섯 개로 정삼각형 네 개를?

골똘히 연구해도 답을 찾지 못했던 이 문제는 2차원 평면에서만 해결하려는 고정관념을 깨고 피라미드 모양으로 성냥개비를 쌓아 올리니 해결되었습니다.

그림 7-2

차원을 달리하니 쉽게 완성!

인공지능 학자들은 인공 신경망을 개발하기 위해서 반드시 XOR 문제를 극복해야만 했습니다. 이 문제 역시 고정관념을 깬 기발한 아이디어에서 해결점이 보였습니다. 그림 7-3은 전혀 새로운 방법으로 이를 해결하는 모습을 보여 줍니다.

그림 7-3

XOR 문제의 해결은 평면을 휘어주는 것!

로 종이를 휘어 주는 것이 답이었습니다. 즉, 좌표 평면 자체에 변화를 주는 것입니다. XOR 문제를 해결하기 위해서 우리는 두 개의 퍼셉트론을 한 번에 계산할 수 있어야 합니다. 이를 가능하게 하려면 숨어있는 층, 즉 은닉층(hidden layer)을 만들면 됩니다.

그림 7-4

퍼셉트론에서 다층 퍼셉트론으로

입력층과 은닉층의 그래프를 집어넣어 보면 그림 7-5와 같습니다. 은닉층이 좌표 평면을 왜곡시키는 결과를 가져옵니다.

그림 7-5

은닉층의 공간 왜곡(https://goo.gl/8qEGHD 참조)

입력 값(input)을 놓고 파란색과 빨간색의 영역을 구분한다고 할 때, 그림 7-5의 왼쪽 그림을 보면 어떤 직선으로도 이를 해결할 수 없습니다. 하지만 은닉층을 만들어 공간을 왜곡하면 두 영역을 가로지르는 선이 직선으로 바뀝니다.

1 다층 퍼셉트론의 설계

다층 퍼셉트론이 입력층과 출력층 사이에 숨어있는 은닉층을 만드는 것을 도식으로 나타내면 그림 7-6과 같습니다.

그림 7-6

다중 퍼셉트론의 내부

가운데 숨어있는 은닉층으로 퍼셉트론이 각각 자신의 가중치(w)와 바이어스(b) 값을 보내고, 이 은닉층에서 모인 값이 한 번 더 시그모이드 함수(기호로 σ라고 표시합니다)를 이용해 최종 값으로 결과를 보냅니다. 은닉층에 모이는 중간 정거장을 노드(node)라고 하며, 여기서는 n1과 n2로 표현하였습니다.

n1과 n2의 값은 각각 단일 퍼셉트론의 값과 같습니다.

n1 = σ(x1w11 + x2w21+b1)

n2 = σ(x1w12 + x2w22 + b2)

위 두 식의 결괏값이 출력층으로 보내집니다. 출력층에서는 역시 시그모이드 함수를 통해 y 값이 정해집니다. 이 값을 y out이라 할 때 식으로 표현하면 다음과 같습니다.

이제 각각의 가중치(w)와 바이어스(b)의 값을 정할 차례입니다. 2차원 배열로 늘어놓으면 다음과 같이 표시할 수 있습니다. 은닉층을 포함해 가중치 6개와 바이어스 3개가 필요합니다.

한 노드당 바이어스 하나를 주는구나..

2 XOR 문제의 해결

앞서 우리에게 어떤 가중치와 바이어스가 필요한지를 알아보았습니다. 이를 만족하는 가중치와 바이어스의 조합은 무수히 많습니다. 이를 구하는 방법은 8장에서 소개할 예정입니다. 지금은 먼저 다음과 같이 각 변숫값을 정하고 이를 이용해 XOR 문제를 해결하는 과정을 알아보겠습니다.

이것을 도식에 대입하면 다음과 같습니다.

그림 7-7

다중 퍼셉트론의 내부에 변수를 채워보자.

이제 x1의 값과 x2의 값을 각각 입력해 y 값이 우리가 원하는 값으로 나오는지를 점검해 보겠습니다.

x1 x2 n1 n2 yout 우리가 원하는 값 0 0 σ(0 * (-2) + 0 * (-2) + 3) ≈ 1 σ(0 * 2 + 0 * 2 – 1) ≈ 0 σ(1 * 1 + 0 * 1 – 1) ≈ 0 0 0 1 σ(0 * (-2) + 1 * (-2) + 3) ≈ 1 σ(0 * 2 + 1 * 2 – 1) ≈ 1 σ(1 * 1 + 1 * 1 – 1) ≈ 1 1 1 0 σ(1 * (-2) + 0 * (-2) + 3) ≈ 1 σ(1 * 2 + 0 * 2 – 1) ≈ 1 σ(1 * 1 + 1 * 1 – 1) ≈ 1 1 1 1 σ(1 * (-2) + 1 * (-2) + 3) ≈ 0 σ(1 * 2 + 1 * 2 – 1) ≈ 1 σ(0 * 1 + 1 * 1 – 1) ≈ 0 0

표 7-1

XOR 다층 문제 해결

TIP

≈ 기호는 ‘거의 같다’를 의미하는 것으로 이해하면 됩니다.

표 7-1에서 볼 수 있듯이 n1, n2, y를 구하는 공식에 차례로 대입하니 우리가 원하는 결과를 구할 수 있었습니다. 숨어있는 두 개의 노드를 둔 다층 퍼셉트론을 통해 XOR 문제가 해결된 것입니다.

3 코딩으로 XOR 문제 해결하기

이제 주어진 가중치와 바이어스를 이용해 XOR 문제를 해결하는 파이썬 코드를 작성해 볼까요?

먼저 표 7-1에서 n1의 값을 잘 보면 입력 값 x1, x2가 모두 1일 때 0을 출력하고 하나라도 0이 아니면 1을 출력하게 되어 있습니다. 이는 표 6-1에서 배운 AND 게이트의 정반대 값을 출력하는 방식입니다. 이를 NAND(Negative And) 게이트라고 부릅니다.

그리고 n2의 값을 잘 보면 x1, x2에 대한 OR 게이트에 대한 답입니다.

NAND 게이트와 OR 게이트, 이 두 가지를 내재한 각각의 퍼셉트론이 다중 레이어 안에서 각각 작동하고, 이 두 가지 값에 대해 AND 게이트를 수행한 값이 바로 우리가 구하고자 하는 Y_out임을 알 수 있습니다.

정해진 가중치와 바이어스를 numpy 라이브러리를 사용해 다음과 같이 선언하겠습니다.

import numpy as np w11 = np.array([-2, -2]) w12 = np.array([2, 2]) w2 = np.array([1, 1]) b1 = 3 b2 = -1 b3 = -1

이제 퍼셉트론 함수를 만들어 줍니다. 0과 1 중에서 값을 출력하게 설정합니다.

def MLP(x, w, b): y = np.sum(w * x) + b if y <= 0: return 0 else: return 1 각 게이트의 정의에 따라 NAND 게이트, OR 게이트, AND 게이트, XOR 게이트 함수를 만들어 줍니다. # NAND 게이트 def NAND(x1, x2): return MLP(np.array([x1, x2]), w11, b1) # OR 게이트 def OR(x1, x2): return MLP(np.array([x1, x2]), w12, b2) # AND 게이트 def AND(x1, x2): return MLP(np.array([x1, x2]), w2, b3) # XOR 게이트 def XOR(x1, x2): return AND(NAND(x1, x2),OR(x1, x2)) 이제 x1과 x2 값을 번갈아 대입해 가며 최종 값을 출력해 봅시다. if __name__ == '__main__': for x in [(0, 0), (1, 0), (0, 1), (1, 1)]: y = XOR(x[0], x[1]) print("입력 값: " + str(x) + " 출력 값: " + str(y)) 모두 정리하면 다음과 같습니다. import numpy as np # 가중치와 바이어스 w11 = np.array([-2, -2]) w12 = np.array([2, 2]) w2 = np.array([1, 1]) b1 = 3 b2 = -1 b3 = -1 # 퍼셉트론 def MLP(x, w, b): y = np.sum(w * x) + b if y <= 0: return 0 else: return 1 # NAND 게이트 def NAND(x1, x2): return MLP(np.array([x1, x2]), w11, b1) # OR 게이트 def OR(x1, x2): return MLP(np.array([x1, x2]), w12, b2) # AND 게이트 def AND(x1, x2): return MLP(np.array([x1, x2]), w2, b3) # XOR 게이트 def XOR(x1, x2): return AND(NAND(x1, x2),OR(x1, x2)) # x1, x2 값을 번갈아 대입하며 최종값 출력 if __name__ == '__main__': for x in [(0, 0), (1, 0), (0, 1), (1, 1)]: y = XOR(x[0], x[1]) print("입력 값: " + str(x) + " 출력 값: " + str(y)) 우리가 원하는 XOR 문제의 정답이 도출되었습니다. 이렇게 퍼셉트론 하나로 해결되지 않던 문제를 은닉층을 만들어 해결했습니다. 은닉층을 여러 개 쌓아올려 복잡한 문제를 해결하는 과정은 뉴런이 복잡한 과정을 거쳐 사고를 낳는 사람의 신경망을 닮았습니다. 그래서 이 방법을 ‘인공 신경망’이라 부르기 시작했고, 이를 간단히 줄여서 신경망이라고 통칭합니다.

[#E10] 딥러닝의 기초 XOR 문제란?

DEEP LEARNING은 기본적으로 NEURAL NETWORK(NN)를 기반으로 하며, 머신러닝을 더욱 완전하게 만드는 방법으로 볼 수 있습니다.

아래의 그림은 x1과 x2 값에 따른 y의 값을 유동적으로 나타내고 있습니다.

그림과 같이 OR, AND 그래프에서는 데이터를 분류할 수 있는 Linear 라인을 정의할 수 있습니다. 그러나 XOR 그래프에서는 불가능합니다.

이러한 XOR 문제를 해결하기 위한 방법이 바로 딥러닝이며, BackPropagation 알고리즘을 사용합니다.

BackPropagation (역전파)

자세한 강의는 링크를 참고하세요.

Deep Learning은 기본적으로 여러개의 Layer를 쌓은 후 학습하여, 실제 Y값과 예측 Y값의 차이 ( Cost )를 구하고 다시 처음 과정으로 돌아가서 변수를 재조정하는 과정을 반복합니다.

이는 곧 Cost Minimize와 같습니다.

이 알고리즘은 우리가 직접 구현할 필요 없이 텐서플로우 내부에서 자동적으로 적용되어 값이 도출됩니다.

따라서 우리는 Layer만 쌓으면 되는데, 이것은 다음과 같이 구성할 수 있습니다.

기존

1 2 3 W = tf.Variable(tf.random_normal([ 2 , 2 ]), name = ‘weight’ ) b = tf.Variable(tf.random_normal([ 2 ]), name = ‘bias’ ) hypothesis = tf.sigmoid(tf.matmul(X, W1) + b1) cs

NeuralNetwork (딥러닝)

1 2 3 4 5 6 7 8 W1 = tf.Variable(tf.random_normal([ 2 , 2 ]), name = ‘weight1’ ) b1 = tf.Variable(tf.random_normal([ 2 ]), name = ‘bias1’ ) layer1 = tf.sigmoid(tf.matmul(X, W1) + b1) W2 = tf.Variable(tf.random_normal([ 2 , 1 ]), name = ‘weight2’ ) b2 = tf.Variable(tf.random_normal([ 1 ]), name = ‘bias2’ ) hypothesis = tf.sigmoid(tf.matmul(layer1, W2) + b2) cs

코드 자체는 굉장히 단순합니다.

W1과 b1으로 layer1을 구성하고, 이를 새로운 X 값으로 생각하고 W2와 다시 매트릭스 곱 및 sigmoid 함수를 이용하여 새로운 hypothesis를 구성합니다.

( sigmoid – y_data는 0과 1로만 구성되어있으므로 Logistic Classification )

주의해야 할 점은 W1에서 보이듯이 출력값이 2개라면 W2가 받는 X데이터의 값 또한 2개여야 합니다.

단, W2의 출력값은 1로 제한되지 않습니다.

이제 XOR 문제를 해결해보겠습니다.

1 2 3 4 x_data = [[0, 0], [0, 1], [1, 0], [1, 1]] y_data = [[0], [1], [1], [0]] Colored by Color Scripter cs

마찬가지로 y_data는 0과 1로만 구성되어있으므로 Logistic Classification의 Cost 함수를 이용합니다.

SOURCE CODE

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 import tensorflow as tf import numpy as np x_data = [[ 0 , 0 ], [ 0 , 1 ], [ 1 , 0 ], [ 1 , 1 ]] y_data = [[ 0 ], [ 1 ], [ 1 ], [ 0 ]] x_data = np.array(x_data, dtype = np.float32) y_data = np.array(y_data, dtype = np.float32) X = tf.placeholder(tf.float32, [None, 2 ]) Y = tf.placeholder(tf.float32, [None, 1 ]) W1 = tf.Variable(tf.random_normal([ 2 , 2 ]), name = ‘weight1’ ) b1 = tf.Variable(tf.random_normal([ 2 ]), name = ‘bias1’ ) layer1 = tf.sigmoid(tf.matmul(X, W1) + b1) W2 = tf.Variable(tf.random_normal([ 2 , 1 ]), name = ‘weight2’ ) b2 = tf.Variable(tf.random_normal([ 1 ]), name = ‘bias2’ ) hypothesis = tf.sigmoid(tf.matmul(layer1, W2) + b2) cost = – tf.reduce_mean(Y * tf.log(hypothesis) + ( 1 – Y) * tf.log( 1 – hypothesis)) train = tf.train.GradientDescentOptimizer(learning_rate = 0. 1 ).minimize(cost) # Accuracy computation # True if hypothesis > 0.5 else False predicted = tf.cast(hypothesis > 0. 5 , dtype = tf.float32) accuracy = tf.reduce_mean(tf.cast(tf.equal(predicted, Y), dtype = tf.float32)) # Launch graph with tf.Session() as sess: # Initialize TensorFlow variables sess.run(tf.global_variables_initializer()) for step in range ( 10001 ): sess.run(train, feed_dict = {X: x_data, Y: y_data}) if step % 100 = = 0 : print (step, sess.run(cost, feed_dict = { X: x_data, Y: y_data}), sess.run([W1, W2])) # Accuracy report h, c, a = sess.run([hypothesis, predicted, accuracy], feed_dict = {X: x_data, Y: y_data}) print ( ”

Hypothesis: ” , h, ”

Correct: ” , c, ”

Accuracy: ” , a) cs

결과

1 2 3 4 5 6 7 8 9 10 11 Hypothesis: [[ 0. 01115024 ] [ 0. 9874386 ] [ 0. 98751473 ] [ 0. 01938552 ]] Correct: [[ 0. ] [ 1. ] [ 1. ] [ 0. ]] Accuracy: 1. 0 cs

학습 결과 다음과 같이 정확하게 결과를 예측했습니다.

즉, Neural Network는 Layer를 deep하게 쌓은 후 학습한다는 의미에서 Deep Learning이라고 합니다.

레이어는 다음과 같이 여러 개를 쌓을 수 있으며, 중요한 것은 항상 이전 레이어의 Y 출력값과 다음 W 변수의 X 입력값이 같아야 한다는 점입니다.

마찬가지로 최종 Y 출력값에는 제한이 없습니다.
[모델1] : DEEP

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 W1 = tf.Variable(tf.random_normal([ 2 , 10 ]), name = ‘weight1’ ) b1 = tf.Variable(tf.random_normal([ 10 ]), name = ‘bias1’ ) layer1 = tf.sigmoid(tf.matmul(X, W1) + b1) W2 = tf.Variable(tf.random_normal([ 10 , 10 ]), name = ‘weight2’ ) b2 = tf.Variable(tf.random_normal([ 10 ]), name = ‘bias2’ ) layer2 = tf.sigmoid(tf.matmul(layer1, W2) + b2) W3 = tf.Variable(tf.random_normal([ 10 , 10 ]), name = ‘weight3’ ) b3 = tf.Variable(tf.random_normal([ 10 ]), name = ‘bias3’ ) layer3 = tf.sigmoid(tf.matmul(layer2, W3) + b3) W4 = tf.Variable(tf.random_normal([ 10 , 1 ]), name = ‘weight4’ ) b4 = tf.Variable(tf.random_normal([ 1 ]), name = ‘bias4’ ) hypothesis = tf.sigmoid(tf.matmul(layer3, W4) + b4) cs
[모델2] : WIDE

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 W1 = tf.Variable(tf.random_normal([ 2 , 248 ]), name = ‘weight1’ ) b1 = tf.Variable(tf.random_normal([ 248 ]), name = ‘bias1’ ) layer1 = tf.sigmoid(tf.matmul(X, W1) + b1) W2 = tf.Variable(tf.random_normal([ 248 , 48 ]), name = ‘weight2’ ) b2 = tf.Variable(tf.random_normal([ 48 ]), name = ‘bias2’ ) layer2 = tf.sigmoid(tf.matmul(layer1, W2) + b2) W3 = tf.Variable(tf.random_normal([ 48 , 10 ]), name = ‘weight3’ ) b3 = tf.Variable(tf.random_normal([ 10 ]), name = ‘bias3’ ) layer3 = tf.sigmoid(tf.matmul(layer2, W3) + b3) W4 = tf.Variable(tf.random_normal([ 10 , 15 ]), name = ‘weight4’ ) b4 = tf.Variable(tf.random_normal([ 15 ]), name = ‘bias4’ ) hypothesis = tf.sigmoid(tf.matmul(layer3, W4) + b4) cs

XOR 문제의 해결, 층 쌓기

목차

XOR 문제 리마인트 XOR 문제 해결 다층 퍼셉트론 (multi-layer perceptron)

1. XOR 문제 리마인드

지난 포스트에서, 풀기 어려운 난제에 대해 이야기한 바가 있다. 문제를 풀기에 앞서, 문제가 무엇인지 리마인드를 해보자.

AND, NAND, OR 게이트 등은 2차원의 공간 상에 표현했을 때, 하나의 선만으로 빨간 동그라미와 파란 세모와의 구역을 구분지을 수 있었다. 예를 들면, 아래는 OR 게이트를 시각화한 것이다.

하지만 XOR 게이트는 하나의 선만을 가지고 구분지을 수가 없었다.

이것을 해결하기 위한 방법이 많지만, 우리는 그 중에서도 가장 간단한, ‘그냥 선 한번 더 그어버리지 뭐’를 사용해보겠다.

2. XOR 문제 해결

‘그냥 선 한번 더 그어버리지 뭐’는 파란 세모들만 영역에 들어오게 하기 위해 선을 두번 그어버리는 수법이다. AND와 NAND, OR 게이트를 모두 시각화해봤을 때, XOR은 OR과 NAND의 겹치는 부위이다. 즉, 어떤 정보가 들어왔을 때 OR 게이트를 거치고 난 정보와 NAND 게이트를 거치고 난 정보를 AND로 조합하면 우리가 원하는 XOR 정답이 나온다는 얘기다.

이것을 진리표로 체크해보면 다음과 같다.

$x_1$ $x_2$ OR($x_1$, $x_2$) NAND ($x_1$, $x_2$) AND(OR, NAND) XOR 0 0 0 1 0 0 1 0 1 1 1 1 0 1 1 1 1 1 1 1 1 0 0 0

위의 표에서 알 수 있듯이, NAND와 OR 게이트를 거친 정보가 AND로 조합되어 최종적으로 XOR과 같은 결과를 보인다는 사실을 알 수 있다. 겨우 4개의 점이 맞냐 아니냐를 판단하는 게 뭐 그리 대수냐고 할 수 있겠지만, 사실 이 XOR 문제 해결의 핵심은 비선형의 문제를 선형 문제의 조합으로 풀 수 있다는 데에 있다.

위의 사항을 파이썬으로 구현해보면 다음과 같다.

def XOR(x1, x2): h1 = OR(x1, x2) h2 = NAND(x1, x2) y = AND(h1, h2) if y > 0 : return 1 else: return 0

(XOR의 구현에는 지난 포스트에서 구현한 OR과 NAND, AND 함수를 이용한다.)

3. 다층 퍼셉트론 (multi-layer perceptron)

XOR 문제를 해결하면서, 우리는 아주 자연스럽게 퍼셉트론의 층을 ‘쌓았다’.

‘쌓았다’라는 말이 직관적으로 와닿지 않을 독자분들을 위해 위에서 한 작업들을 시각적으로 표현해보면 다음과 같다.

지난번의 단층 퍼셉트론과 비교했을 때, 회색 층이 한층 늘어난 것을 볼 수 있다.

이것이 인공 신경망(Neural Network) 아이디어의 시초이다. 즉, 판가름하는 단층의 게이트들을 ‘쌓고 조합해서’ 복잡한 판가름을 해보자는 얘기다.

정리

여기까지 잘 따라왔다면, ‘그렇다면 다층 퍼셉트론이 곧 인공신경망이라는 얘기인가?’하는 적절한 의문을 던질 수 있겠다. 물론 퍼셉트론이 인공신경망의 시초라는 찬사로 장을 열긴 했다. 하지만, $x_1$과 $x_2$의 XOR 게이트를 구현하는 데에만 6개의 가중치와 3개의 편향, 즉 9개의 변수를 결정해야 하는데, 층이 더 많아지고 노드($x_n$)가 더 많아지면, 이걸 언제 일일이 계산하고 앉아있겠나?

이걸 해결하기 위해 신경망의 학습법이 등장한다. 신경망의 ‘학습’에 대해 이해하기 전에, 신경망이 어떤 존재인지 먼저 다음 포스트에서 짚고 넘어가보자.

So you have finished reading the xor 문제 topic article, if you find this article useful, please share it. Thank you very much. See more: XOR 문제 해결, 다층 퍼셉트론 예제, 단층퍼셉트론, 다층 퍼셉트론 딥러닝 차이, 퍼셉트론 가중치 계산

Top 50 Xor 문제 The 14 Correct Answer

[인공지능]다층 퍼셉트론으로 XOR문제 해결하기

[#E10] 딥러닝의 기초 XOR 문제란?

XOR 문제의 해결, 층 쌓기

딥러닝 01 – 기초 정리 XOR 문제 해결 과정

11. 단층 퍼셉트론의 한계-1.XOR 문제

인공지능의 암흑기를 열었던 퍼셉트론의 XOR 문제 : 네이버 블로그

딥러닝 Neural Network AND 함수, XOR 문제 해결 방법

퍼셉트론 – XOR (exclusive OR) 문제

[인공지능]다층 퍼셉트론으로 XOR문제 해결하기

[#E10] 딥러닝의 기초 XOR 문제란?

XOR 문제의 해결, 층 쌓기

Leave a Comment Cancel reply